Meer bijzonderheden van de Simson-lijn

Overzicht  ][ De lijn van Simson | Meetkunde | Cabri

Zie ook de pagina "De lijn van Simson en een enveloppe"
Zie ook de pagina "Generalisaties van de Simson-lijn"
Zie ook  het Cabri-werkblad "De lijn van Simson"
Zie ook de pagina "Over de Siimson-lijn van het Steiner-punt en van het Tarry-punt"

Overzicht terug

  1. Vooraf - enkele hulpstellingen cabrisignal
  2. Eigenschappen van de Simson-lijn  cabrisignal
  3. Constructies
  4. S-driehoeken cabrisignal
  5. Orthopool cabrisignal
  6. Constructie van de orthopool
  7. Bijzondere s-lijnen en een driehoek gevormd door s-lijnen
  8. s-lijnen van een punt tov. twee driehoeken cabrisignal
  9. De Simson-lijn en de Steiner-lijn cabrisignal
      
  10. Download

1. Vooraf - enkele hulpstellingen terug
We gaan in hetgeen volgt uit van een driehoek ABC met omcirkel O. Voor een punt P van de omcirkel geven we de Simson-lijn aan met s(P); maw. indien gesproken wordt over een Simson-lijn s(P), dan ligt P op de omcirkel.
We bewijzen nu:

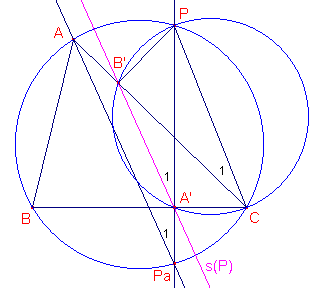
Stelling 1a
Is Pa het tweede snijpunt van de loodlijn uit P naar de zijde BC met de omcirkel, dan is voor iedere P:
APa // s(P).
.
figuur 1 sims1 Bewijs:
s(P) gaat door de projectie A' van P op BC en door de projectie B' van P op AC.
Nu is in vierhoek PB'A'C: PB'C = PA'C = 90º. PB'A'C is dus een koordenvierhoek, waaruit volgt:
C1 = A'1 (omtrekshoeken, beide op boog PB').
Ook is C1 = Pa,1 (omtrekshoeken, beide op boog PA van de omcirkel), zodat
Pa,1 = A'1
waaruit het gestelde volgt. ¨

Klik hier Applet voor een CabriJavapplet bij Stelling 1a.

Gevolgen:
[1]
Uit Stelling 1a volgt een snelle constructie van de lijn s(P) bij een punt P.
[2]
Met Stelling 1a in verband staand:

Stelling 1b
ALS:
Ha' is het snijpunt van de hoogtelijn uit A (op BC) met de omcirkel,
Q het snijpunt van PHa' met BC
DAN:
QH // s(P).

Bewijs: zie figuur 2.

figuur 2 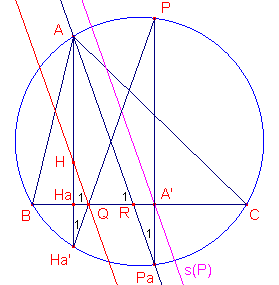sims2 Nu is Ha',1 = Pa,1 (omtrekshoeken op gelijke bogen), waaruit onmiddellijk volgt: Q1 = R1 (omdat immers HHa = HaHa').
En hieruit volgt het gestelde. ¨

[einde Gevolg]

Stelling 2
Voor ieder P geldt dat s(P) door het midden gaat van het lijnstuk PH.

Bewijs: zie figuur 3.

figuur 3 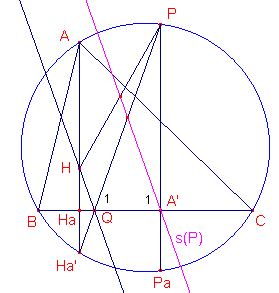sims3 s(P) gaat ook door het midden van PQ, immers in de rechthoekige driehoek PA'Q hebben we vanwege de symmetrie: A1 = Q1. Dus s(P) is zwaartelijn naar de hypothenusa van  driehoek PA'Q.
Omdat s(P) // HQ (zie Stelling 1b), gaat s(P) dus ook door het midden van PH (middenparallel in driehoek PHa'H). ¨

Opmerking
Het midden van PH ligt op de negenpuntscirkel van ABC, immers die cirkel is het beeld van de omcirkel bij vermenigvuldiging met ½ tov. het punt H.
[einde Opmerking]

2. Eigenschappen van de Simson-lijn terug

Stelling 3
De hoek tussen de lijnen s(P1) en s(P2) is gelijk aan ½bg(P1P2).

Bewijs: zie figuur 4.

figuur 4 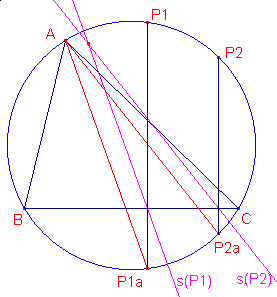sims41 De hoek tussen s(P1) en s(P2) is gelijk aan de hoek tussen P1a en P2a. Deze hoek is gelijk aan ½bg(P1aP2a) = ½bg(P1P2). ¨

Gevolg van Stelling 3:

figuur 5 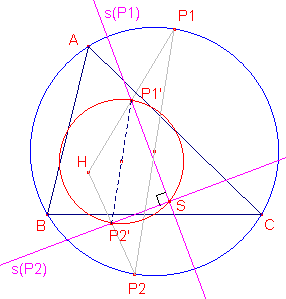sims4
Stelling 4
[1] De Simson-lijnen van twee tegenpunten P1 en P2 op de omcirkel van driehoek ABC staan loodrecht op elkaar.
[2] De snijpunten van deze lijnen liggen op de negenpuntscirkel van driehoek ABC.

Bewijs:
[1]
Dit volgt onmiddellijk uit Stelling 3.
[2]
s(P1) gaat door het midden P1' van HP1; s(P2) gaat door het midden P2' van HP2.
Bij vermenigvuldiging met ½ van de omcirkel tov. H gaat deze over in de negenpuntscirkel. P1P2 is dus een middellijn van de negenpuntscirkel. P1SP2 = 90° (zie [1]).

Volgens de Stelling van Thales ligt S dus op de cirkel met middellijn P1P2, ic. op de negenpuntscirkel. ¨

Klik hier Applet voor een CabriJavapplet bij Stelling 4.

Gevolg van Stelling 4:

figuur 6 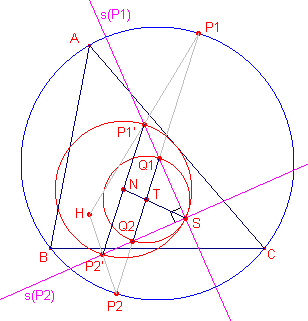sims6
Stelling 5
De snijpunten Q1 en Q2 van s(P1) en s(P2) met de lijn P1P2 zijn de eindpunten de middellijn van een cirkel die raakt aan de negenpuntscirkel.

Bewijs: zie figuur 6.
Het punt S ligt op de negenpuntscirkel (zie Stelling 4). Het midden N van P1'P2' is het middelpunt van de negenpuntscirkel.
Nu is: P1'P2' // Q1Q2, waaruit volgt dat NS de lijn P1P2 snijdt in het midden T van Q1Q2. De cirkels N en T raken elkaar dus. ¨

 

3. Constructies terug

3.1. Construeer een Simson-lijn met een gegeven richting terug

Uitvoering

figuur 7a 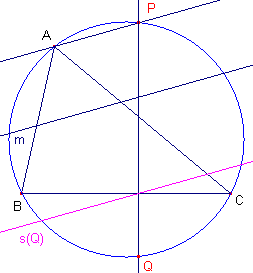sims7a De gegeven richting wordt aangegeven door de lijn m.
1 - Lijn door A evenwijdig met m. Deze lijn snijdt de omcirkel in een tweede punt P.
2 - Lijn door P loodrecht op BC (die lijn is evenwijdig met ha).
3 - Deze lijn snijdt de omcirkel in een tweede punt Q.
4 - De s-lijn van Q is de gevraagde Simson-lijn. ¨

Opmerking
Uit de constructie volgt, dat er precies één s-lijn is met een gegeven richting.
[einde Opmerking]

3.2. Construeer een Simson-lijn loodrecht op een gegeven lijn (gegeven richting) terug

Uitvoering

figuur 7b 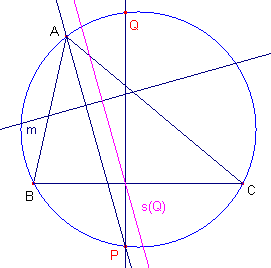sims7b [1] - eerste constructie
De gevraagde lijn is de Simson-lijn behorende bij het tegenpunt van het punt Q uit de vorige constructie.
[2] - tweede constructie
De gegeven lijn zij m.
1 - Loodlijn door A op m. Deze lijn snijdt de omcirkel in een tweede punt P.
2 - Loodlijn op BC uit P geeft een tweede punt Q op de omcirkel.
3 - De s-lijn van Q is de gevraagde Simson-lijn. ¨

Opmerking
Er is precies één s-lijn loodrecht op een gegeven richting.
[einde Opmerking]

3.3. Derde Simson-lijn door het snijpunt van twee Simson-lijnen terug

Uitvoering en bewijs

figuur 7c 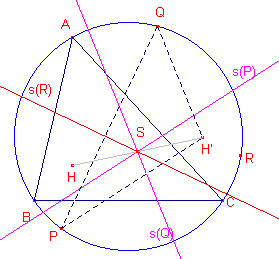simson31 s(P) en s(Q) zijn de Simson-lijnen van P en Q bij driehoek ABC. H is het hoogtepunt van ABC. Beide s-lijnen snijden elkaar in het punt S.
1. H' is het beeld van H bij puntspiegeling in S.
2. R is het hoogtepunt van driehoek PQH'.
3. s(R) is de gevraagde derde s-lijn door S. ¨

Bewijs:
We dienen aan te tonen, dat R op de omcirkel van ABC ligt en dat s(R) door S gaat.
Vanwege de ligging van H' hebben we:
PH' // s(P) en QH' // s(Q).
De hoek tussen PH' en QH' is dus gelijk aan de hoek tussen s(P) en s(Q) en deze is gelijk aan ½bg(PQ); zie Stelling 3.

Laten we nu loodlijnen neer uit P op QH' en uit Q op PH' dan snijden deze (hoogtelijnen) elkaar in een punt R van de omcirkel; immers hoek PRQ is dan gelijk aan ½bg(PQ).
Maar nu is H' het hoogtepunt van driehoek PQR. s(R) is dan evenwijdig aan RH' en gaat dus ook door S. ¨

Opmerking
Zie voor de naamgeving van driehoeken als ABC en PQR de paragraaf S-driehoeken en in het bijzonder Stelling 9.
[einde Opmerking]

4. S-driehoeken terug

Definitie
Indien van een driehoek A'B'C' die ingeschreven is in de omcirkel van driehoek ABC, geldt dat de s-lijn (tov. ABC) van tenminste één van de hoekpunten (A', B' of C') loodrecht staat op de overstaande zijde (in A'B'C'), dan heet A'B'C' S-driehoek van ABC.
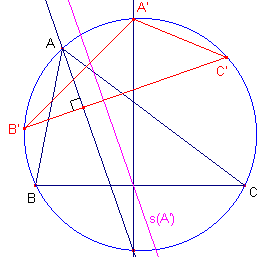sims8a Voorbeeld
In de hiernaast staande figuur is s(A') _|_ B'C'.
A'B'C' is dus volgens de definitie een S-driehoek van ABC.
De constructie van een S-driehoek kan dus verlopen volgens de hierboven in paragraaf 3.2 gegeven beschrijving.
Uit deze constructie volgt de juistheid van de bewering.
[einde Voorbeeld]
Stelling 6
Voor een S-driehoek A'B'C' van ABC geldt voor de bogen AA', BB', CC' op de omcirkel, dat
bg(AA') + bg(BB') + bg(CC') = 0
mits de bogen doorlopen worden in dezelfde richting (dus alle positief of alle negatief).

Bewijs: zie figuur 8.

figuur 8 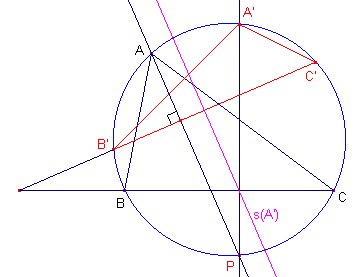sims8b In nevenstaande figuur is:
Ð(BC, B'C') = Ð(AP, A'P), immers de benen van de ene hoek staan loodrecht op die van de andere.
Dus:
bg(CC') - bg(B'B) = bg(A'A)
of, en  van teken voorzien:
bg(A'A) + bg(B'B) + bg(CC') = 0
Bij alle andere mogelijke liggingen verloopt het bewijs analoog. ¨
Stelling 7
[1] Geldt voor een S-driehoek A'B'C' van driehoek ABC dat s(A') _|_ B'C', dan is ook
s(B') _|_ A'C' en s(C') _|_ A'B'.
[2] De lijnen s(A'), s(B'), s(C') zijn concurrent.

Klik hier klik hier voor een CabriJavapplet bij Stelling 7.

Bewijs: zie figuur 9.

figuur 9 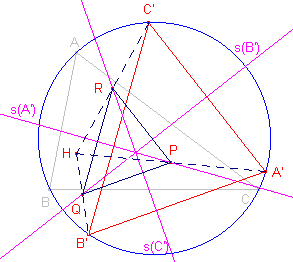sims9 [1]
Dit volgt uit Stelling 6, immers bij de constructie van van de s-lijn die loodrecht staat op A'C' vinden we (als enige mogelijkheid het punt B'.
[2]
Zij P, Q, R de middens van de lijnstukken HA', HB', HC'.
De beschouwde s-lijnen zijn dan hoogtelijnen van driehoek PQR en zijn dus concurrent. ¨

Opmerking
Driehoek PQR heeft de negenpuntscirkel van driehoek ABC als omcirkel.
[einde Opmerking]
Stelling 8
Is A'B'C' een S-driehoek van ABC, dan is ABC een S-driehoek van A'B'C'.

Bewijs:
Dit volgt onmiddellijk uit Stelling 6. ¨

Gevolg:

figuur 10 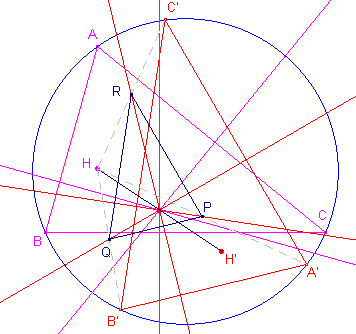sims10
Stelling 9
Het snijpunt van de s-lijnen van twee S-driehoeken ABC en A'B'C' is het midden van het lijnstuk HH', waarbij H en H' de hoogtepunten zijn van de driehoeken.

Bewijs:
Het bedoelde snijpunt is het beeld van H' bij vermenigvuldiging met ½ van driehoek A'B'C' tov. H (met beelddriehoek PQR). Het beeld is dus het midden van HH'. ¨

Klik hier klik hier voor een CabriJavapplet bij Stelling 9.
Stelling 10a
Voor twee S-driehoeken P1Q1R1 en P2Q2R2 van ABC zijn geldt dat P1Q1R1 ook S-driehoek is van P2Q2R2 (en omgekeerd).
We spreken daarom ook wel van een stelsel S-driehoeken of ook wel S-stelsel.

Bewijs:
Volgens Stelling 6 geldt
(1)...... bg(AP1)+bg(AQ1)+bg(AR1) = 0
(2)...... bg(AP2)+bg(AQ2)+bg(AR2) = 0
Aftrekking van (1) en (2) geeft: bg(P1P2)+bg(Q1Q2)+bg(R1R2) = 0
Waaruit het gestelde volgt. ¨

figuur 11 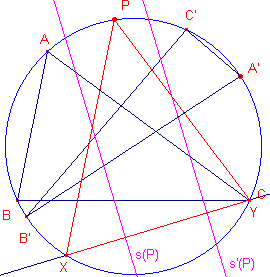sims11
Stelling 10b
De s-lijnen s(P) van een punt P tov. van een S-stelsel driehoeken hebben een vaste richting.

Bewijs:
De lijn s(P) staat loodrecht op de overstaande zijde van P van driehoek PXY.
De s-lijnen van P tov. elke driehoek uit het S-stelsel dus ook. Ze hebben dus een vaste richting. ¨

Zie ook Stelling 18.

5. Orthopool terug

Stelling 11a
De projecties van de punten A, B, C van een driehoek op een willkeurige lijn m zijn A', B', C'.
De loodlijnen door A', B', C' op BC, CA en AB gaan door één punt.
Dit punt heet de orthopool van m tov. driehoek ABC.

Klik hier klik hier voor een CabriJavapplet bij Stelling 11a.

Bewijs: zie figuur 12a.

figuur 12a 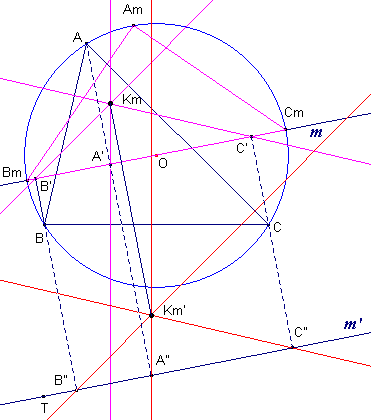sims12 [1]
We gaan er eerst van uit, dat de lijn m de omcirkel van ABC snijdt in de punten Bm en Cm (m gaat bijvoorbeeld door O).
De loodlijnen op de zijden zijn nu niets anders dan de s-lijnen van A', B', C' tov. een driehoek waarvan BmCm een zijde is (zie driehoek AmBmCm in figuur 12a).
Volgens Stelling 7 zijn deze lijnen concurrent (in het punt Km).
Km is dus de orthopool van BmCm.
[2]
Stel de lijnen m' // BmCm snijdt de omcirkel niet.
Tov. de eerste situatie is er nu een translatie over d(m, m') die de lijnen A'Km, B'Km, C'Km afbeeldt op daarmee evenwijdige lijnen door A", B", C" (de projecties van A, B, C op m'). Deze lijnen gaan dus ook door een punt Km'. ¨

Gevolg:

Stelling 11b
De orthopool van een middellijn van de omcirkel ligt op de negenpuntscirkel van ABC.
figuur 12b 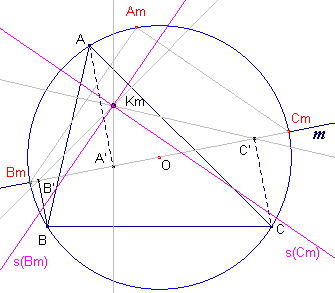sims12b Bewijs: zie figuur 12b.
Zijn Bm en Cm bedoelde eindpunten, dan gaan de s-lijnen s(Bm) en s(Cm) door het punt Km (de orthopool); zie Stelling 11a (onderdeel [1] van het bewijs daar). De beide lijnen staan loodrecht op elkaar en het snijpunt Km ligt dus op de negenpuntscirkel (zie Stelling 4.2). ¨

Klik hier klik hier voor een CabriJavapplet bij Stelling 11b.

Opmerking
Zie ook de pagina "Voetpuntsdriehoeken" in verband met het zogenoemde Feuerbach-punt"
[einde Opmerking]
Stelling 12a
De projecties A', B', C' van de hoekpunten A, B, C op een middellijn van de omcirkel van ABC zijn het spiegelbeeld van hetzelfde punt K in de zijden van de centrumdriehoek MaMbMc van ABC.
Het punt K is de orthopool van die middellijn tov. driehoek ABC.

Bewijs: zie figuur 13.

figuur 13a 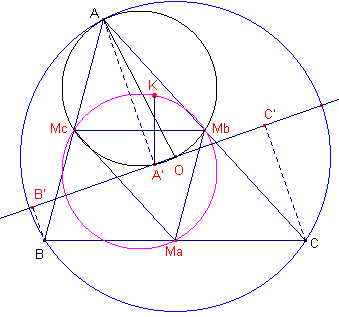sims13 AA' _|_ B'C'. A' ligt dus op de cirkel met middellijn AO (Thales-cirkel). Omdat OMb _|_ AC (en OMc _|_ BA) ligt ook Mb (en Mc) op deze cirkel.
Deze cirkel is het spiegelbeeld van de negenpuntscirkel in MbMc.
Zij nu K de orthopool van B'C' (een middellijn van de omcirkel).
Uit de constructie van K volgt, dat de lijn KA' _|_ BC.
Dus ook KA' _|_ MbMc.
K ligt op de negenpuntscirkel (Stellling 11b).
Het beeld van K ligt dus op de cirkel met middellijn AO.
K en A' zijn dus elkaars spiegelbeeld bij spiegeling in MbMc.
Analoog geldt dit voor K en B' en voor K en C'. ¨

Gevolg:

Stelling 12b
De lijn s-lijn van K tov. de centrumdriehoek van driehoek ABC is evenwijdig met B'C' en deelt het lijnstuk OK middendoor.

Bewijs: zie figuur 13b.

figuur 13b 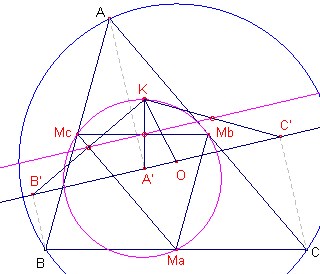sims13b De  projecties van K op de zijden van driehoek MaMbMc (de centrumdriehoek, die de negenpuntscirkel als omcirkel heeft), vallen samen met de middens van de lijnstukken  KA', KB', KC' (zie Stelling 12a). s(K, MaMbMc) is dus middenparallel in driehoek KB'C' en daardoor evenwijdig met B'C'. Het lijnstuk OK wordt door s(K) middendoor gedeeld. ¨

Opmerkingen
[1]
B'C' valt nu samen met OI.
[2]
Zie ook Stelling 10 en Stelling 11 op de pagina "Voetpuntsdriehoeken".
[einde Opmerkingen]
Stelling 13
ALS
de middellijn d snijdt de zijden  BC, CA, AB in de punten Ad, Bd, Cd.
DAN
de cirkels met middellijnen AAd, BBd, CCd gaan door de orthopool K van d.

Bewijs: zie figuur 14.

figuur 14 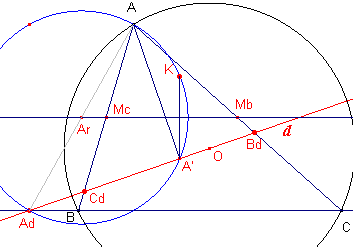sims14 We bekijken alleen de cirkel met middellijn AAd.
Het middelpunt zij Ar. MbMc (zijde van de centrumdriehoek) gaat door Ar (middenparallel).
MbMc is dus middellijn van de cirkel.
Het punt A' (de project van A op d) ligt op cirkel Ar (Thales-cirkel).
Het spiegelbeeld van A' in MbMc is K (orthopool van d). K ligt dus ook op de cirkel Ar.
We bewijzen analoog voor de beide andere cirkels. ¨

6. Constructie van de orthopool van een lijn tov. een driehoek terug

Uitvoering

figuur 15 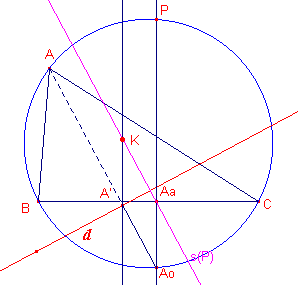sims15 Zij d de gegeven lijn.
1 - A' is de projectie van A op d.
2 - Ao is het snijpunt van de projecterende met de omcirkel.
3 - Aa is het voetpunt van de loodlijn uit Ao op BC.
4 - K is het 4e hoekpunt van het parallellogram A'AoAaK.
K is de orthopool van d tov. ABC. ¨

Opmerking
Is P het snijpunt van AoAa met de omcirkel, dan ligt K op s(P), waaruit een tweede constructie volgt, als s(P) gegeven (geconstrueerd) is.
[einde Opmerking]

7. Bijzondere s-lijnen en een driehoek gevormd door s-lijnen terug

7.1. Bijzondere s-lijnen terug

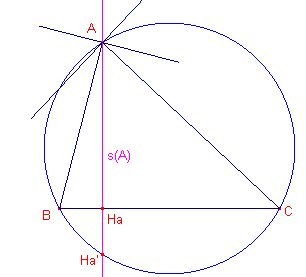
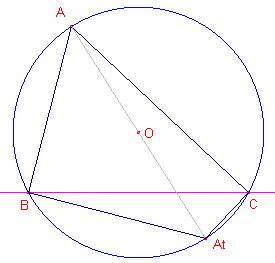
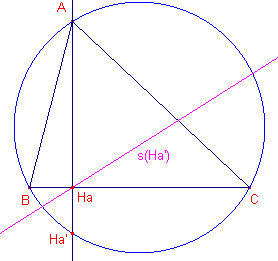
Stelling 14a
[1] De s-lijnen van de hoekpunten van ABC zijn de hoogtelijnen
[2] De s-lijnen van de tegenpunten van de hoekpunten van ABC zijn de zijden van ABC.
[3] De s-lijnen van de snijpunten van de hoogtelijnen met de omcirkel van ABC zijn evenwijdig met de raaklijnen in A, B, C aan de omcirkel en gaan door de hoekpunten van de voetpuntsdriehoek
figuur 16a figuur 16b figuur 16c
sims16a sims16b sims16c

Bewijs:
[1]
We bewijzen met de "definitie" van s-lijn van een punt.
Het snijpunt van de loodlijnen uit A op AB en AC valt samen met A.
Het voetpunt van de loodlijn op BC is Ha.
De s-lijn van A is dus de lijn AHa, de hoogtelijn uit A.
[2]
We bewijzen met de "definitie" van s-lijn van een punt.
Zij At het tegenpunt van A.
De loodlijn uit At op AB valt samen met B (Thales-cirkel). De loodlijn uit At op AC valt samen met C.
BC is de s-lijn van At.
[3]
We bewijzen met behulp van de constructie uit Stelling 1a.
De lijn HaA staat loodrecht op BC. Het snijpunt met de omcirkel is A. We moeten dus A met zichzelf verbinden om de richting van de s-lijn van Ha te vinden. Die richting is de richting van de raaklijn.
De s-lijn zelf gaat door Ha.
De s-lijnen van de punten Ha', Hb' en Hc' vormen dus de voetpuntsdriehoek van ABC. ¨

Stelling 14b
De s-lijnen van de snijpunten van de bissectrices van ABC met de omcirkel gaan door de middens van de overstaande zijden en staan loodrecht op die bissectrices.
figuur 17 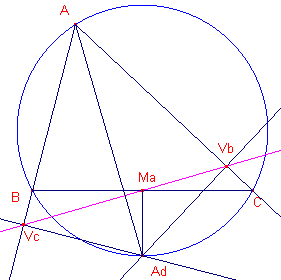sims17 Bewijs:
De projectie van Ad op BC is het midden van BC.
De s-lijn van Ad gaat dus door Ma.
De voetpunten Vb en Vc op AB en AC vormen de vlieger AVcAdVb.
De diagonalen daarvan staan loodrecht op elkaar. ¨

7.2. Een driehoek gevormd door s-lijnen terug
We beschouwen in deze paragraaf twee driehoeken ABC en A'B'C' met dezelfde omcirkel.
De lijnen s(A'), s(B'), s(C') tov. ABC zijn de zijden van een derde driehoek PQR.

figuur 18 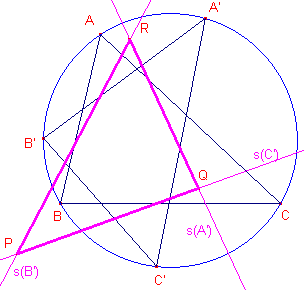sims18
Stelling 15
Driehoek PQR is gelijkvormig met driehoek A'B'C'.

Bewijs:
Volgens Stelling 3 is Ð(s(B'), s(C')) = ½ bg(B'C') = ÐA'.
Enzovoorts.  ¨

Klik hier klik hier voor een CabriJavapplet bij Stelling 15.
Stelling 16
Het middelpunt S van de omcirkel van PQR valt samen met het midden van het lijnstuk HH' (verbindingslijnstuk van de hoogtepunten van ABC en A'B'C'.
figuur 19a 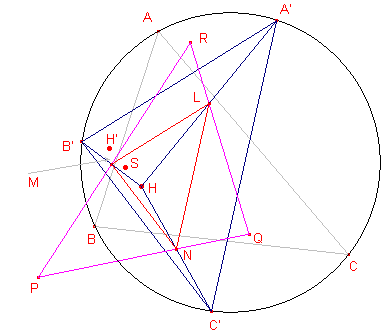sims19 Bewijs:
Zijn L,M,N de middens van HA', HB', HC'.
Nu is driehoek LMN homothetisch met A'B'C (centrum van vermenigvuldiging H, factor ½).
Het hoogtepunt van LMN is het midden S van HH'.
Maar dan ook LMN ~ PQR (zie Stelling 15).
Driehoek PQR is een omgeschreven driehoek van LMN en is ermee gelijkvormig.
We moeten nu aantonen, dat het punt S (hoogtepunt van LMN) middelpunt is van de omcirkel van PQR
figuur 19b 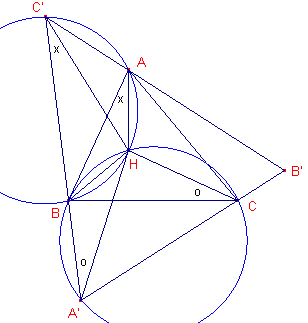sims19b We tonen hiernaast aan (in algemene zin), dat dit juist is.
Driehoek ABC is ingeschreven in driehoek A"B"C', waarbij A = A', B = B', C = C'.
Hieruit volgt, dat A'CHB en C'BHA koordenvierhoeken zijn (in de laatste is: BHC = 180-A = 180-A').
Hieruit volgt dus de gelijkheid van de hoeken die in figuur 19b zijn aangegeven met dezelfde tekens (omtrekshoeken op dezelfde cirkelboog).
In driehoek ABC is echter ook:
HAB = HCB = 90-B.
Zodat driehoek A'HC' twee gelijke hoeken heeft.
Dus is HA' = HC'.
Analoog: HA' = HB'.
Waaruit blijkt dat H het omcentrum is van A'B'C'. ¨ 

Gevolg:

figuur 20 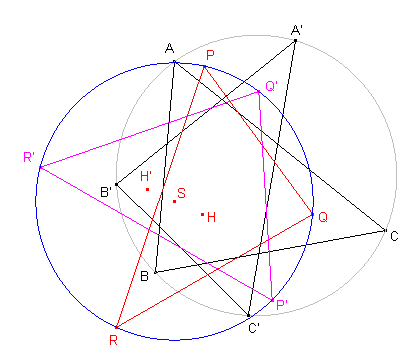sims20
Stelling 17
Driehoek PQR ontstaat uit A', B', C' tov. ABC en driehoek P'Q'R' ontstaat uit A, B, C tov A'B'C'.
PQR en P'Q'R' hebben dezelfde omgeschreven cirkel.

Bewijs:
Dit volgt onmiddellijk uit Stelling 16. ¨ 

Klik hier klik hier voor een CabriJavapplet bij Stelling 17.

8. s-lijnen van een punt tov. twee driehoeken terug

Stelling 18 (Droz-Farny)
Zijn ABC en A'B'C' twee driehoeken met dezelfde omcirkel, dan is de hoek tussen s(P) en s'(P) constant voor iedere P.
figuur 21 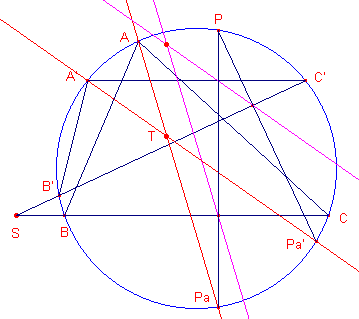sims21 Bewijs:
Zij S het snijpunt van BC en B'C'.
Nu geldt PPa _|_ BC en PPa' _|_ B'C'. De hoek tussen PPa en PPa' is dus gelijk aan de hoek S.
Hoek S is constant.
Nu geldt verder (zie Stelling 1a), dat
s(P) // APa en s'(P) // A'Pa'.
De hoek tussen de beide s-lijnen is dus gelijk aan de hoek tussen APa en A'Pa' (met snijpunt T).
Nu geldt: T = ½(bg(AA') + bg(PaPa')) = ½(bg(AA') + 2S).
Hoek T is dus constant. ¨ 

Zie ook Stelling 10b.

Klik hier klik hier voor een CabriJavapplet bij Stelling 18.

9. De Simson-lijn en de Steiner-lijn terug

Stelling 19
[1] De drie spiegelbeelden van een punt P van de omcirkel van driehoek ABC in de zijden van die driehoek liggen op dezelfde rechte lijn.
Deze lijn heet de Steiner-lijn van P bij de driehoek (naar Jakob Steiner, 1796-1863, Zwitserland).
[2] De Steiner-lijn van een punt (van de omcirkel) bij een driehoek gaat door het hoogtepunt H van die driehoek.

Opmerking
Deze stelling is eveneens, maar op een iets afwijkende manier, bewezen op de pagina "De lijn van Steiner"
[einde Opmerking]

Bewijs:

figuur 22 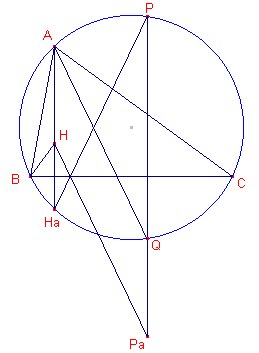simson30 We bewijzen allereerst iets over het hoogtepunt van de driehoek in samenhang met de Simson-lijn s(P) van een punt P.
In figuur 22 is H het hoogtepunt van driehoek ABC. Pa is het spiegelbeeld van P (op de omcirkel) in de lijn BC. PPa snijdt de omcirkel ook in Q.
Zoals bekend is Ha (het snijpunt van de hoogtelijn uit A met de omcirkel) het spiegelbeeld van H in de lijn BC (zie bijvoorbeeld de pagina "Een eigenschap van het hoogtepunt").
Nu is wegens de spiegelsymmetrie:
Ð HaPPa = Ð HPaP
en
Ð HaAQ = Ð HaPPa (omtrekshoeken op dezelfde boog)
Voorts is bg(HaQ) = bg(AP).
Uit dit alles volgt eenvoudig dat AQ // HPa.

Uit Stelling 1a volgt dan, wegens AQ // s(P), dat HPa // s(P) ......(1)
figuur 23 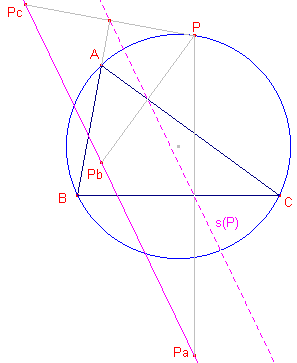simson30b Uit de constructie van de spiegelbeelden van P in de zijden volgt, dat de punten Pa, Pb, Pc op dezelfde rechte lijn liggen.
Immers, bij een vermenigvuldiging met factor 2 tov. het punt P gaan de voetpunten van de loodlijnen uit P op deze zijden over in de punten Pa, Pb, Pc.
De Steiner-lijn van P is dus het beeld van de Simson-lijn van P bij die vermenigvuldiging .

We hebben dus Simson(P) // Steiner(P).

Uit (1) volgt dan, omdat Pa ook op HPa ligt met HPa // s(P), dat de Steiner-lijn van P door het hoogtepunt H van de driehoek gaat. ¨ 

Klik hier klik hier voor een CabriJavapplet bij Stelling 19.

¤ Zie ook de pagina "De lijn van Simson en een enveloppe"
¤ Zie ook de pagina "Generalisaties van de Simson-lijn"
¤ Zie ook de pagina "Over de Siimson-lijn van het Steiner-punt en van het Tarry-punt"
¤ Zie ook de pagina "Koordenvierhoeken voor de s-lijnen van de hoekpunten van een koordenvierhoek.

10. Download terug
De figuren die gebruikt zijn in de CabriJavapplets op deze pagina kunnen in één bestand via deze website worden gedownload.
In dit bestand zijn ook opgenomen de macro's: SimsonLijn.mac, SpuntLijn.mac en Orthopool.mac.
Klik hier om het downloaden te starten (ZIP-bestand, ca. 12kB)

begin pagina

[simson2.htm] laatste wijziging op: 09-08-02