Over de Simson-lijn van het Steiner-punt en van het Tarry-punt
Overzicht ][ Brocard-hoek | Brocard-driehoeken | Brocard-punten | Simson-lijn | Meetkunde
- Overeenkomstige zijden in een driehoek en diens 1e Brocard-driehoek
- Simson-lijnen en wat hoeken
- Simson-lijnen bij het Steiner-punt en het Tarry-punt

1.
Overeenkomstige zijden in een driehoek en diens 1e Brocard-driehoek ![]()
We schrijven op deze pagina ter vereenvoudiging: dbg(X) =
½bg X .
We bewijzen nu een eigenschap mbt. de overeenkomstige zijden in bedoelde driehoeken:
| Stelling 1a In driehoek A met 1e Brocard-driehoek B is de hoek tussen A2A3 en B2B3 gelijk aan de hoek tussen KO en OA1, waarbij K het Lemoine-punt is van driehoek A. |
Bewijs:
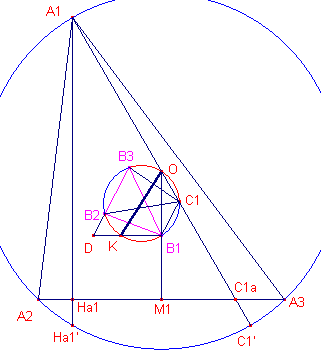 |
In de hiernaast staande figuur is: - B1B2B3 (driehoek B) de 1e Brocard-driehoek van A1A2A3 (driehoek A). - K het Lemoine-punt van driehoek A - O het middelpunt van de omcirkel van driehoek A - K het Lemoine-punt van driehoek A. Zij nu C1
het tweede snijpunt van A1O met de Brocard-cirkel. |
|
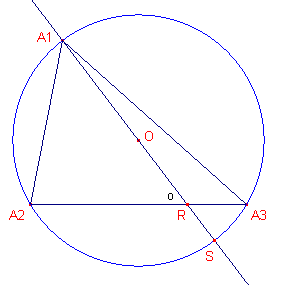 |
Bewijs:
|
2. Simson-lijnen en wat hoeken
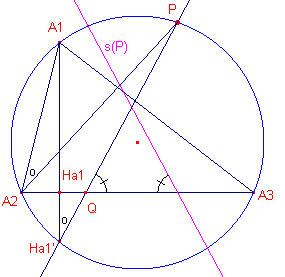 |
Bewijs:
|
Bewijs:
In driehoek QHa1Ha1' is Q = 90°- Ha1' =
90° - PA2A1. Dus,
Q = 90° - (A2 - PA1A2)
¨
[einde Gevolg]
| Stelling 3 [1] De hoek die de Simson-lijn van P maakt met OA1 is gelijk aan PA2A3 - A3. [2] De hoek tussen PA1 en A2A3 is gelijk aan PA2A3 - A3. |
Bewijs:
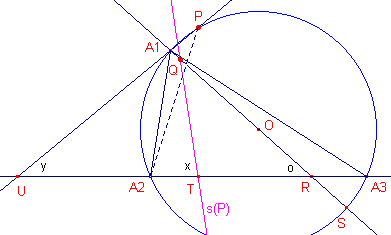 |
[1] In de figuur hiernaast:bekijken we driehoek TRQ (Q is het snijpunt van s(P) met OA1). Buitenhoek T = TQR + TRQ (som van twee binnenhoeken) Buitenhoek T = 90° - (A2 - PA1A2), zie het Gevolg van Stelling 2 TRQ = A3 + (90° - A2), zie Stelling 1b Dus: 90° - (A2 - PA1A2) = TRQ + A3 + (90° - A2) Zodat: TRQ = PA1A2 - A3 ¨ |
[2]
PA1 snijdt A2A3 in U. Nu is:
y = dbg(PA3) - dbg(A1A2) = PA2A3
- A3
¨
3. Simson-lijnen bij het Steiner-punt en het Tarry-punt
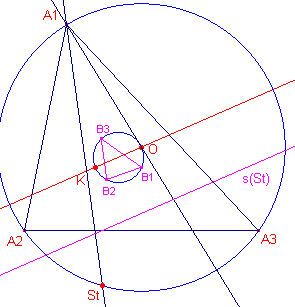 |
We kiezen nu het Steiner-punt
St en bepalen daarvan de Simson-lijn, s(St). Het punt St wordt gevonden als snijpunt van de omcirkel met de lijn door A1 evenwijdig met B2B3. Uit het bovenstaande vinden we nu: De hoek die s(St) maakt met OA1, is gelijk aan StA2A3 - A3 = Ð (StA1, A2A3) = Ð (B2B3, A2A3) De hoek die OK maakt met OA1 is dus gelijk aan de hoek die s(St) maakt met OA1. De lijnen OK en s(St) zijn dus evenwijdig.
|
|
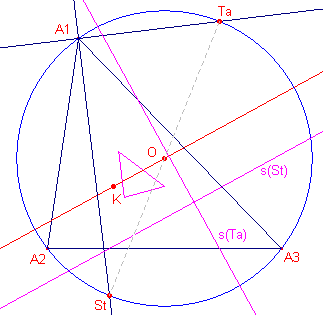 |
Bewijs: |