Constructie van de Brocard-hoek

Overzicht  ][  Brocard-punten | Brocard-driehoeken | Meetkunde

Overzicht terug

  1. Constructie
  2. Gevolgen
  3. Eenvoudige constructie van het 1e Brocard-punt

1. Constructie terug
Op de pagina "Punten van Brocard" is de Brocard-hoek geïntroduceerd door het 1e Brocard-punt mbv. in een hoekpunt aan de zijden van de driehoek rakende cirkels te construeren.
Hieronder (en in paragraaf 3) volgt een eenvoudiger constructie van de Brocard-hoek.

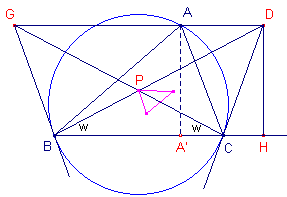
brocardh1 We gaan uit van de raaklijnen CD en BG in C en B aan de omcirkel.
Deze lijnen snijden de lijn door A evenwijdig met BC in D en G.
- ACD = ABC (omtrekshoeken op dezelfde boog)
- DCH = A (de hoeken C, B, A vormen in C een gestrekte hoek)
Zij nu DBC = w.
Dan is ook GCB = w (CDGB is een gelijkbenig trapezium).
Zij verder DH = h.

BH = h cot w ......(1)
CH = h cot DCH = h cot A

BC = BA' + A'C = h cot B + h cot C
BH = BC + CH = h (cot A + cot B + cot C) ......(2)
Uit (1) en (2) volgt dan:
cot w = cot A + cot B + cot C (zie de pagina "Punten van Brocard", Stelling 8)
w is dus (inderdaad) de Brocard-hoek van de driehoek. ¨

Opmerking
Deze constructie is gegeven door Brocard (Henri Brocard, 1845-1922, Frankrijk) in Nouvelles Correspondances mathématiques (ed. M.E.C. Catalan) in 1880.
Referentie:
F.G.-M.: Excercices de Géométrie, Editions Jaques Gabay (reprint 1991, Sceaux)
[einde Opmerking]

2. Gevolgen terug
[1]
Het punt P in bovenstaande figuur, het snijpunt van BD en CG, is een hoekpunt van de 1e Brocard-driehoek.

[2]
De lijn DG is een zijde van de anticomplementaire driehoek van ABC (zijden door de hoekpunten evenwijdig met de overstaande zijde van zo'n hoekpunt).
De lijn CD is een zijde van de raaklijndriehoek van ABC (de zijden zijn de raaklijnen in de hoekpunten aan de omcirkel).

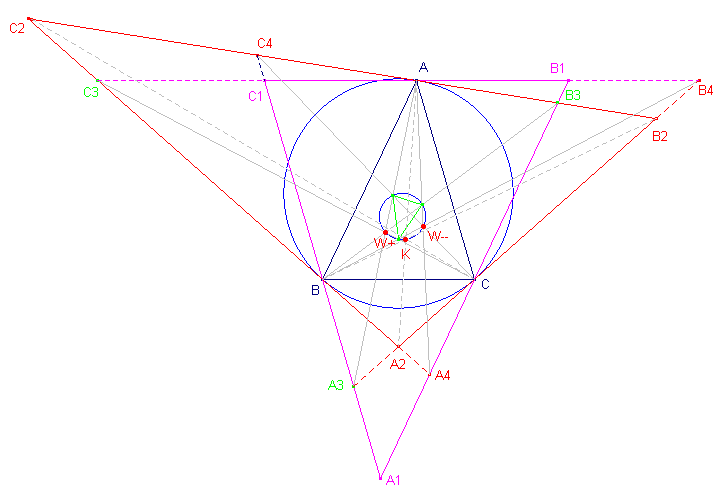
brocardh2
In bovenstaande figuur is A1B1C1 de anticomplementaire driehoek van ABC.
Driehoek A2B2C2 is de raaklijndriehoek van ABC.
Dus:
telkens een zijde van de ene driehoek en een zijde van de andere driehoek bepalen zes snijpunten, te weten A3, B3, C3 en A4, B4, C4.
De lijnen AA3, ... zijn concurrent in het 1e Brocard-punt, W+, van ABC.
De lijnen AA4, ... zijn concurrent in het 2e Brocard-punt, W-, van ABC.
Verder:
De lijnen AA2, ... zijn concurrent in het Lemoine-punt, K, van ABC (zie Stelling 10 op de pagina "Isogonale verwantschap").

3. Eenvoudige constructie van het 1e Brocard-punt terug
Voor de constructie van een punt P waarvoor geldt PBC = PCA = PAB (het 1e Brocard-punt) is het voldoende een cirkel te beschrijven waarop (bijvoorbeeld) het segment p - A te vinden is met als koorde AC.
Dit is de cirkel die raakt in A aan AB en ook gaat door C.

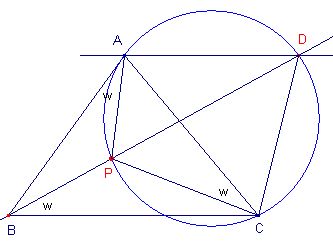brocardh3 Zij D het van A verschillende snijpunt van deze cirkel en de lijn door A evenwijdig met BC.
En zij P het van D verschillende snijpunt van BD met die cirkel.
Nu is:
PAB = PCA = ADP (omtrekshoeken op dezelfde cirkelboog)
Maar ook ADP = PBC (Z-hoeken).
Dus:
PAB = PBC = PCA.
P is dus het 1e Brocard-punt van ABC.

En hiermee is ook eenvoudig de Brocard-hoek van ABC geconstrueerd. ¨

Opmerkingen
[1]
Zie ook de pagina Punten van Brocard, Stelling 7 oa. in verband deze constructie.

[2]
Deze constructie is voor het eerst (?) gepubliceerd in het boek van A. EMMERICH: Die Brocardsche Gebilde (1895).
[einde Opmerkingen]

terug
[brocardhoek.htm] laatste wijziging op: 26-04-04