Brocard-driehoeken

Overzicht  ][  Brocard-punten | Brocard-cirkel | Isogonale verwantschap | Meetkunde

Zie ook de pagina "Constructie van de Brocard-hoek"
Zie ook de pagina "Gelijkvormigheid (van drie figuren)"

Overzicht terug

  1. Definitie 1e Brocard-driehoek cabrisignal
  2. Het 3e Brocard-punt cabrisignal
  3. Zwaartepunt
  4. Definitie 2e Brocard-driehoek cabrisignal
  5. Steiner-punt en Tarry-punt cabrisignal
  6. Referenties
  1. Download

1. Definitie 1e Brocard-driehoek terug

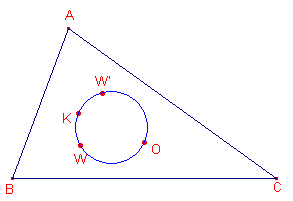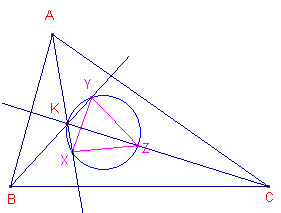
brocardd1 We gaan uit van een driehoek ABC met daarin de beide Brocard-punten W en W'.
De cirkel door W, W', K (Lemoine-punt) en O (omcentrum) is de zogenoemde Brocard-cirkel van driehoek ABC.
Een middellijn van de Brocard-cirkel is KO.
De lijn KO heet de Brocard-as van de driehoek (naar Henri Brocard, 1845-1922, Frankrijk).

 
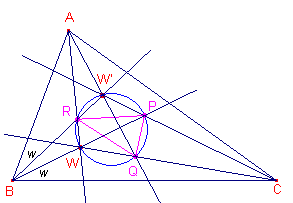
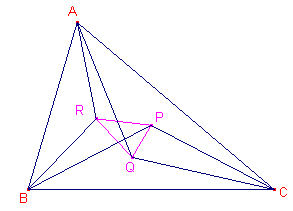
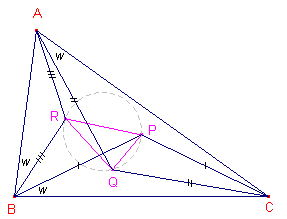
brocardd2 We bekijken nu de driehoek waarvan de hoekpunten P, Q, R de tweede snijpunten van opvolgend BW, CW, AW met de Brocard-cirkel zijn.
PQR heet 1e Brocard-driehoek van ABC.
(Zie eventueel ook de pagina "Constructie van de Brocard-hoek").

Opmerking
We gebruiken dus het 1e Brocard-punt om driehoek PQR te genereren.
Als we het 2e Brocard-punt gebruiken vinden we dezelfde driehoek. Zie hiervoor Stelling 2.
[einde Opmerking]
Stelling 1
De hoekpunten van de 1e Brocard-driehoek zijn de, van O verschillende, snijpunten van de Brocard-cirkel met de middelloodlijnen van de driehoek.

Klik hier Animatie voor een CabriJavapplet bij deze stelling.

Bewijs:
Voor het punt Lemoine-punt K geldt, dat de afstanden ervan tot de zijden evenredig zijn met die zijden (zie Stelling 8 op de pagina "Isogonale verwantschap").
De evenredigheidsfactor is gelijk aan p = 2F /(a2 + b2 + c2) (zie het Gevolg van Stelling 8 op de pagina "Isogonale verwantschap").
Hierin is F de oppervlakte van driehoek ABC.
Verder weten we dat voor de Brocard-hoek w geldt: cot w = (a2+b2+c2) / 4F (zie Stelling 11 op de pagina "Punten van Brocard").
Zodat p = ½ tan w.
De afstand van K tot BC is dus gelijk aan ½ a tan w.

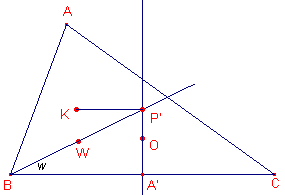brocardd3 Zij nu P' het snijpunt BW en de middelloodlijn van BC. Nu is WBC = w.
A' is het midden van BC, zodat
tan w = P'A' / BA', waaruit volgt dat P'A' = ½ a tan w.
P' en K hebben dus dezelfde afstand tot BC, waaruit volgt dat KP' // BC.
KP'O is dus gelijk aan 90º. P' ligt dus op de Brocard-cirkel. Maar P' ligt ook op BW, zodat
P = P'. Analoog voor Q = Q' en R = R'.
Waaruit het gestelde volgt. ¨

 
brocardd5
Stelling 2
De 1e Brocard-driehoek PQR wordt ook bepaald door de lijnen CW', AW', BW'

Bewijs:
Uit Stelling 1 volgt dat PBC gelijkbening is. PBC = w.
Zodat ook PCB = w.
Volgens de definitie van W' ligt dus W' op CP. ¨

 
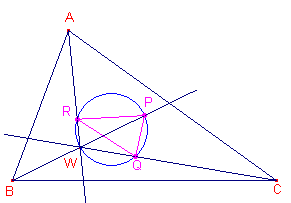
Gevolg
De driehoeken PQR (1e Brocard-driehoek) en ABC zijn gelijkvormig (indirect).

Bewijs:

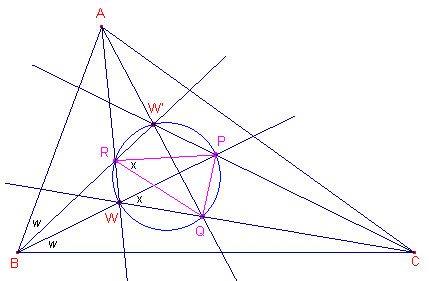brocardd5b PQRW is een koordenvierhoek. Hierin is nu
PRQ = PWQ = x (omtrekshoeken op dezelfde cirkelboog).
Nu is verder WCA = w, waaruit
WCB = C - w
Volgens de stelling van de buitenhoek hebben we in driehoek WBC:
buitenhoekW = x = WBC + WCB = w + (C - w) = C,
zodat ook
PRQ = C
Analoog bewijzen we dat in driehoek PQR: P =A en Q = B.
Waaruit het gestelde volgt. ¨

 

2. Het 3e Brocard-punt terug

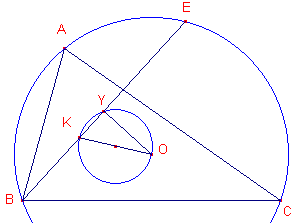
Stelling 3
- Een driehoek en diens 1e Brocard-driehoek zijn perspectief.
- Het perspectiefpunt is het isotomisch verwante punt van K, het Lemoine-punt, tov. de driekoek.
Het perspectiefpunt wordt wel 3e Brocard-punt genoemd.

Bewijs:

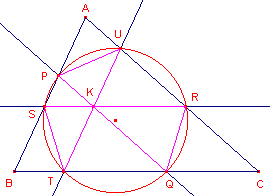ptucklem2 We gebruiken hierbij een eigenschap van de 1e Lemoine-cirkel (zie de figuur hiernaast).
Deze cirkel gaat door de zes snijpunten van de drie met de zijden evenwijdige lijnen door het punt K.
Op de pagina "Tucker-cirkels" is bewezen (klik hier voor het bewijs), dat het midden van KO (het middelpunt van de Brocard-cirkel dus) het middelpunt van de 1e Lemoine-cirkel is.
De snijpunten van de lijn door K evenijdig met BC (de punten R en S) spelen in het volgende deel van het bewijs een belangrijke rol.

 
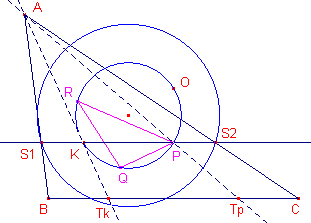brocardd6 De lijn door K evenwijdig met BC snijdt de andere zijden in S1 en S2 (dit zijn de punten R en S in de figuur hierboven).
Deze lijn gaat door P (zie het bewijs van Stelling 1).
S1 en S2 zijn punten van de 1e Lemoine-cirkel. Deze cirkel is concentrisch met de Brocard-cirkel.
Nu is KS1 = PS2, en dus ook TkB = TpC.
ATk en ATp zijn dus isotomisch verwante lijnen (tov. ABC).
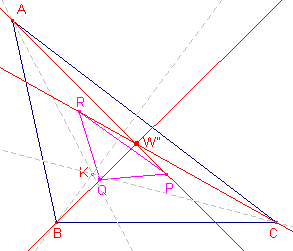brocardd6b De lijnen AK, BK, CK en de daarmee isotomisch verwante lijnen (AP, BQ en CR) bepalen dus twee isotomisch verwante punten, K en het daarmee isomische verwante punt.

Het met K isotomisch verwante punt is dus het 3e Brocard-punt (Kimberling [2]: X76) van de driehoek.. ¨

Klik hier Animatie voor een CabriJavapplet bij deze eigenschap.

Opmerking
Op de pagina "Bijzondere gelijkvormige driehoeken" staat een bewijs van het eerste deel van Stelling 3 (de perspectiviteit) via de Stelling van Kiepert.
[einde Opmerking]

3. Zwaartepunt terug

Stelling 4a
Een driehoek en diens 1e Brocard-driehoek hebben hetzelfde zwaartepunt.

Bewijs:

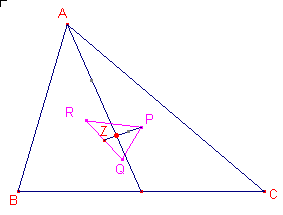brocardd7a brocardd7 Uit het bewijs van Stelling 1 volgt:
PBC ~ QCA ~ RAB,
immers deze driehoeken zijn gelijkbenig en hebben elk twee (basis)hoeken w.

Volgens een opmerkelijke stelling (4b) die we hieronder formuleren, hebben nu PQR en ABC hetzelfde zwaartepunt (zie linker figuur).

 
Stelling 4b
Als de driehoeken PBC, QCA, RAB direct gelijkvormig zijn en "op dezelfde manier gelegen" zijn tov. ABC, dan valt het zwaartepunt van PQR samen met dat van ABC.

¤ Klik hier voor het bewijs van Stelling 4b. ¤

Opmerking

simtri3 "Op dezelfde manier gelegen" kan worden opgevat als: twee van de drie driehoeken zijn uit de derde ontstaan door een draaivermenigvuldiging in tegengestelde richtingen.

De drie driehoeken bij 1e Brocard-driehoek en driehoek ABC voldoen hieraan (zie de figuur hiernaast).

[einde Opmerking en einde Bewijs van Stelling 4a] ¨

Gevolg
Als P, Q, R collineair zijn, dan gaan de lijnen BP, CQ en AR door het zwaartepunt van driehoek ABC.

4. Definitie 2e Brocard-driehoek terug
We gaan nu uit van het Lemoine-punt (K) van een driehoek en bekijken nu opnieuw snijpunten van hoekstransversalen met de Brocard-cirkel.

brocardd8 De driehoek waarvan de hoekpunten X, Y, Z de tweede snijpunten van opvolgend BK, CK, AK met de Brocard-cirkel zijn, heet 2e Brocard-driehoek van ABC.
  
Stelling 5a
Zijn D, E, F de eindpunten van de koorden AK, BK, CK van de omcirkel van ABC, dan zijn X, Y, Z (de hoekpunten van de 2e Brocard-driehoek) de middens van die koorden.

 
brocardd8b Bewijs:
We bekijken de situatie voor het punt Y, dat het midden moet zijn van BE.

Nu is KO middellijn van de Brocard-cirkel. In driehoek KYO is dan hoek Y gelijk aan 90º (Thales-cirkel op KO).
YO staat loodrecht op de koorde BE van de omcirkel. Y is dus het midden van die koorde. ¨

Klik hier Animatie voor een CabriJavapplet bij deze stelling.

Een andere benadering van 2e Brocard-driehoek vinden we in de volgende Stelling.

Stelling 5b
De hoekpunten van de 2e Brocard-driehoek zijn centra van draaivermenigvuldigingen waarmee de zijden van de driehoek op elkaar kunnen worden afgebeeld.

Bewijs:

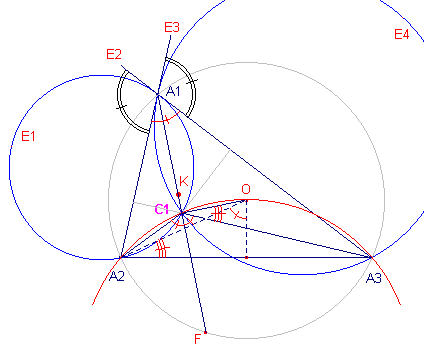brocardd11 C1 is het centrum van vermenigvulding waarbij A3A1 wordt afgebeeld op A1A2.
De constructie van C1 geschiedt met twee cirkels:
- cirkel door A1 en A3 die A1A2 in A1 raakt;
- cirkel door A1 en A2 die A1A3 in A1.
C1 is het van A1 verschillende snijpunt van deze cirkels.
Door deze afbeelding zijn de driehoeken C1A3A1 en C1A1A3 direct gelijkvormig met factor a3 / a2.
Ook de afstanden van C1 tot A3A1 en A1A2 verhouden zich nu als a2 : a3, waardoor de lijn A1C1 de symmediaan van A1 is (K, het Lemoine-punt van A1A2A3)  ligt dus op de lijn A1C1).
Nu is
A1C1A2 = ½bg(A2E1A1) = A2A1E2
A1C1A3 = ½bg(A1E4A3) = A3A1E3
A2A1E2 en A3A1E3 zijn overstaande hoeken (raking), zodat
A1C1A2 = A1C1A3 = 180º - A1
Dus: A2C1A3 = 2A1.
C1 ligt dus op de cirkel A2OA3.
Uit de figuur (zie tekens in de hoeken) volgt nu eenvoudig, dat OC1A1 = 90º.

C1 is dus het midden van de koorde A1F van de omcirkel van A1A2A3.
Nu is volgens Stelling 5a C1 een hoekpunt van de 2e Brocard-driehoek. ¨

Opmerking
Bij het beschouwen van gelijkvormige figuren in een bijzondere ligging (zoals de driehoeken C1A3A1, C1A1A2 in Stelling 5b) blijken de driehoeken van Brocard vaker een belangrijke rol te spelen.
Zie hiervoor de pagina "Gelijkvormigheid"; zie bijvoorbeeld Stelling 2b op die pagina.
[einde Opmerking]

5. Steiner-punt en Tarry-punt terug
B1B2B3 is de 1e Brocard-driehoek van driehoek A1A2A3. Nu geldt:

Stelling 6
De lijnen door A1, A2, A3 evenwijdig met B2B3, B3B1, B1B2 zijn concurrent in het punt S op de omcirkel van A1A2A3.
Het punt S heet het Steiner-punt van de driehoek (Kimberling [2]: X99).
(naar Jakob Steiner, 1796-1863, Zwitserland)

Bewijs:

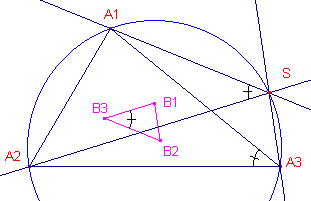brocardd9 Zij S het snijpunt van bedoelde lijnen door A1 en A2. Dan is een hoek bij S gelijk aan hoek B3, die weer gelijk is aan hoek A3 (zie merktekens in de figuur).
Lijnstuk A1A2 wordt onder gelijke hoeken uit S en A3 gezien.
S ligt dus op de omcirkel van A1A2A3.
We bekijken nu ook SA3.
Uit S wordt A2A3 gezien onder dezelfde hoek als uit A1. De hoek tussen SA2 en SA3 is dus gelijk aan A1, en dus gelijk aan hoek B1. Omdat SA2 // B1B3, is dus ook SA3 // B1B2.
Waarmee de concurrentie in S is aangetoond. ¨
brocardd9b
Gevolg
De lijnen door A1, A2, A3 loodrecht op B2B3, B3B1, B1B2 zijn concurrent op omcirkel van A1A2A3, en wel in het tegenpunt T van het Steiner-punt.
Het punt T heet het Tarry-punt van de driehoek (Kimberling [2]: X98).
(naar Gaston Tarry, 1843-1913, Frankrijk)

Klik hier Animatie voor een CabriJavapplet met het Steiner- en Tarry-punt.
Opmerking
Zie de pagina "Over de Simson-lijn van het Steiner-punt en van het Tarry-punt" voor bijzonderheden over de Simson-lijnen van deze twee punten.
[einde Opmerking]
  
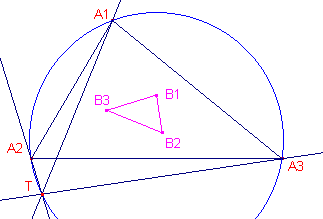
Stelling 7
- Het Lemoine-punt van een driehoek is het Steiner-punt van de 1e Brocard-driehoek van die driehoek.
- Het omcentrum van een driehoek is het Tarry-punt van de 1e Brocard-driehoek van die driehoek.

Bewijs:

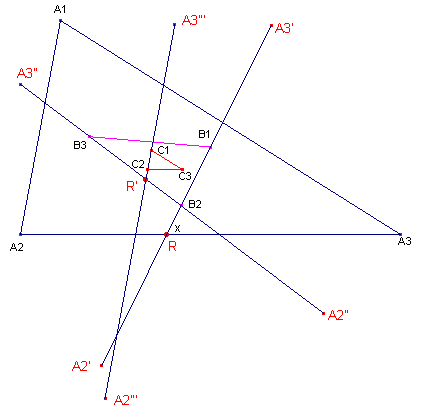brocardd10b Het Gevolg van Stelling 2 zegt dat de 1e Brocard-driehoek (driehoek B) indirect gelijkvormig is met de driehoek (driehoek A).
De 1e Brocard-driehoek (driehoek C) van driehoek B is dus direct gelijkvormig met de oorspronkelijke driehoek.

We tonen allereerst aan, dat de zijden van driehoek C evenwijdig zijn met de zijden van driehoek A.
We voeren enkele rotaties uit.
(1)
Centrum R, hoek A3RB1 = x
Het beeld van A2A3 ligt dan langs B1B2 (lijnstuk A2'A3').
(2)
Centrum B2, hoek A2 (die gelijk is aan hoek B2 in driehoek B)
Het beeld van A2'A3' ligt dan langs B2B3 (lijnstuk A2"A3").
(3)
Centrum R', hoek -x
Het beeld van A2"A3" ligt dan langs C1C2 (lijnstuk A2"'A3"').
De totale rotatie is dan x + A2 - x = A2.
A2"'A3"' maakt dus een hoek ter grootte van A2 met A2A3.
Dus C1C2 // A1A2.
Enzovoorts...
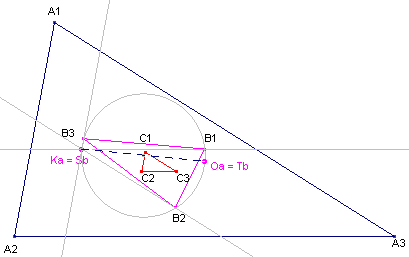brocardd10 Het Steiner-punt Sb van driehoek B vinden we door lijnen door B1, B2, B3 te tekenen die evenwijdig zijn met de zijden van driehoek C (de 1e Brocard-driehoek van driehoek B).
Deze lijnen zijn ook evenwijdig met de zijden van driehoek A (zie eerste deel van dit bewijs).
Uit het bewijs van Stelling 1 volgt dan dat deze lijnen door Ka (het punt van Lemoine van driehoek A) gaan.
Dat dan Oa = Tb volgt onmiddellijk (Oa is immers het tegenpunt van Ka op de 1e Brocard-cirkel van driehoek A). ¨

 

6. Referenties terug

[1]      ROGER A. JOHNSON: Advanced Euclidean Geometry (Dover Publications, New York, 1960)
[2] CLARK KIMBERLING: Triangle Centers and Central Triangles (Winnipeg, Canada, 1998)
[3] CLARK KIMBERLING: "Encyclopedia of Triangle Centers - ETC" - University of Evansville, USA
[4] AAD GODDIJN: Tien punten op één cirkel, in Euclides 77 (4), januari 2002, pp. 150-155

7. Download terug
Enkele Cabri-figuren van deze pagina en de in de applets gebruikte figuren, alsmede een aantal daarbij behorende Cabri-macro's, kunnen in één bestand via deze website worden gedownload.
Klik hier om het downloaden te starten (ZIP-bestand; ca. 23kB).

begin pagina
[brocarddrieh.htm] laatste wijziging op: 26-04-04