Verband tussen de Brocard-punten, het Lemoine-punt en een Miquel-punt

Overzicht  ][  Brocard | Lemoine | Miquel | Meetkunde

Zie ook de pagina "Brocard-driehoeken"

Overzicht

1. Cirkel van Lemoine terug
We gaan uit van het punt van Lemoine van een driehoek.
Door dat punt trekken we (de) drie lijnen die antiparallel zijn met de zijden en snijden die lijnen met de zijden.
We vinden dan

Stelling 1
De snijpunten van de met de zijden antiparallelle lijnen die door het point van Lemoine gaan, met de zijden, zijn concyclisch.
De cirkel heet cirkel van Lemoine (de tweede cirkel van Lemoine).

Bewijs: zie figuur 1.

figuur 1  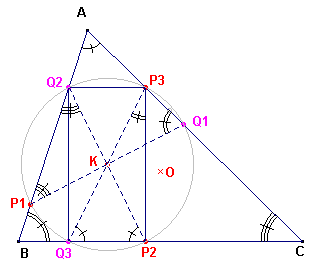bromile1 K is het punt van Lemoine van de driehoek.
De lijnstukken P1Q1, P2Q2, P3Q3 zijn antiparallel met de zijden van de driehoek. Daaruit volgt gelijkheid van hoeken aangegeven in de figuur.
Zo is
   ÐA = ÐP3Q3C (P3Q3 ap AB)
   ÐA = ÐP2Q2B (P2Q2 ap AC)
Dus DKP2Q3 is gelijkbenig: KP2 = KQ3.
Maar de antiparallellen worden door de symmedianen middendoor gedeeld (zie Stelling 5 op de pagina "Isogonalen").
K is dus het midden van alle lijnstukken PiQi.
Dus KP2 = KQ3 = KQ2 = KP3.
P2Q3Q2P3 is dus een rechthoek die een omgeschreven cirkel heeft (met middelpunt K).

Uit de gelijkheid van de met ÐB en ÐC overeenkomende hoeken volgt dan dat alle vanuit K getrokken lijnstukken gelijk zijn.
De zes punten liggen dus op een cirkel, die de (tweede) cirkel van Lemoine (Emile Lemoine, 1840-1912, Frankrijk) wordt genoemd. ¨

Opmerking
Een algemene behandeling van de beide Lemoine-cirkels staat op depagina "Tucker-cirkels".
De beide Lemoine-cirkels komen ook aan de orde op het Cabri-werkblad "Parallel en antiparallel".
[einde Opmerking]

2. Twee driehoeken terug
De zes concyclische punten vallen uiteen in twee deelverzamelingen P1, P2, P3 en Q1, Q2, Q3.
Hiervoor geldt

Stelling 2
De driehoeken P1P2P3 en Q1Q2Q3 zijn congruent en beide gelijkvormig met driehoek ABC.

Bewijs: zie figuur 2.

figuur 2  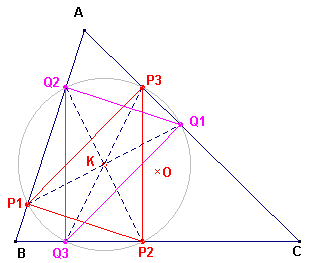bromile2 De punten liggen op de cirkel van Lemoine met middelpunt K (zie Stelling 1)
Passen we nu een puntspiegeling met centrum K toe op P1P2P3, dan gaat deze over in Q1Q2Q3.
Dus DP1P2P3 @ DQ1Q2Q3

P1, P2, Q2 liggen op een Thales-cirkel (middelpunt is het midden van P2Q2). Dus ÐP2P1Q2 = 90º. Dus
  P2P1 ^ AB
Evenzo:
  P1P3 ^ AC
  P3P2 ^ BC
Dus DP1P2P3 ~ DABC
waaruit samen met het eerste deel van het bewijs het gestelde volgt.¨

3. Een Miquel-configuratie geeft een punt van Brocard terug
Drie punten die elk (willekeurig) op een zijde van een driehoek liggen bepalen een zogenoemde Miquel-configuratie. In dit geval kijken we naar de configuratie (P1P2P3, ABC).
De stelling van Miquel zegt nu dat de Miquel-cirkels door één  punt gaan, het punt van Miquel van de configuratie.
We vinden nu een bijzondere eigenschap van dat punt van Miquel :

Stelling 3
Het Miquel-punt van de Miquel-configuratie (P1P2P3, ABC) is een punt van Brocard van driehoek P1P2P3 én ook van driehoek ABC.

Bewijs: zie figuur 3.

figuur 3  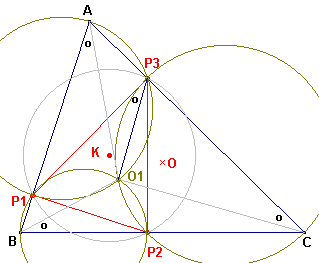bromile3 O1 is het punt van Miquel bij de configuratie (P1P2P3, ABC).
P1P2 raakt aan de Miquel-cirkel op AB en gaat door P3;
P2P3 raakt aan de Miquel-cirkel op BC en gaat door P1
P3P1 raakt aan de Miquel-cirkel op CA en gaat door P2..
Maar dit zijn juist de cirkels waarmee het punt van Brocard van driehoek P1P2P3 wordt geconstrueerd (zie Stelling 7 op de pagina "De punten van Brocard").
O1 is dus een punt van Brocard van driehoek P1P2P3.

O1P3 is een "Brocard-lijnstuk"; dus ÐO1P3P1 = w .
A en P3 liggen op de Miquel-cirkel van AB.
De hoeken O1AP1 en O1P3P1 staan beide op boog O1P1.

Dus ook ÐO1AB = w .
O1 is dus eveneens een punt van Brocard van driehoek ABC. ¨

Gevolg
We kunnen nu driehoek P1P2P3 onderwerpen aan een rotatie met centrum O1 en hoek -90º (wijzerrichting).
Hierdoor komen ABC en het beeld P1'P2'P3' van P1P2P3 in homothetische ligging (zie figuur 4).

figuur 4  bromile4 Hieruit volgt
   O1P1' / O1A = O1P1 / O1A = tan w (zie driehoek O1P1A)
Dus
   O1P1 = O1A . tan w
De gelijkvormigheidsfactor van ABC naar P1P2P3 is dus tan w .
Voor de stralen van de omcirkels geldt dan evenzeer
   r1 = R . tan w
waarin r1 en R opvolgend de straal van de cirkel van Lemoine en de straal van de omcirkel van ABC is.
En ook
   O1K = O1O . tan w
[einde Gevolg]

4. Het tweede punt van Brocard erbij, de cirkel van Brocard terug
Op dezelfde manier als hierboven, in paragraaf 3, voor O1 gedaan is, kunnen we een afleiding geven voor het tweede punt van Brocard, O2.
Zie figuur 5.

figuur 5  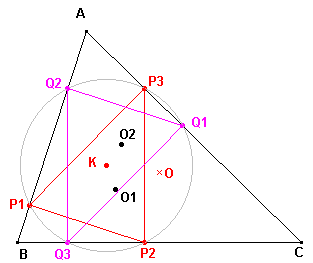bromile5 Voor O2 geldt dan natuurlijk ook
   O2K = O2O . tan w 

Uit het feit, dat OO1 = OO2 (dit is een eigenschap van de beide Brocard-punten; zie Stelling 8 op de pagina "Punten van Brocard"), kunnen we dus concluderen
   KO1 = KO2

We kunnen nu de volgende stelling (Stelling 4) met betrekking tot O, O1, O2 en K bewijzen.
 
Stelling 4
De punten O, O1, O2, K liggen op een cirkel met middellijn OK.
Deze cirkel heet de cirkel van Brocard.

Bewijs: zie figuur 6.

figuur 6  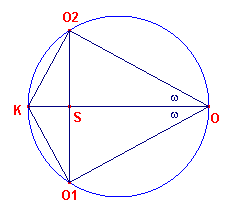bromile6 Zoals we gezien hebben (in het tweede deel van Stelling 3) kunnen we de figuur in homothetische ligging plaatsen door een rotatie om O1 over een hoek van -90º (wijzrrichting). Het beeld van K ligt dan op OO1. hierbij
Dus
   ÐKO1O = 90º
en dus eveneens
   ÐKO2O = 90º
Uit
   O1K = O1O . tan w
volgt dan verder, dat de beide hoeken bij O gelijk zijn aan de hoek van Brocard w .

De punten O, O1, K, O2 zijn dus de hoekpunten van een koordenvierhoek.
Waarmee het gestelde is aangetoond.¨

Opmerking
Zie ook de pagina Brocard-driehoeken waarop enkele andere eigenschappen van de Brocard-cirkel worden behandeld.
[einde Opmerking]

Gevolg
In driehoek OO1S is dan (zie weer figuur 6)
   sin w = SO1 / OO1
zodat
   SO1 = OO1 . sin w
en dan ook
   SO2 = OO2 . sin w
Er is dus sprake van dezelfde factor, sin w , die de gelijkvormigheidsfactor is van de voetpuntsdriehoeken van de punten van Brocard tov. driehoek ABC (zie Stelling 8.1 op de pagina "De punten van Brocard").
Deze voetpuntsdriehoeken hebben dus beide dezelfde omcirkel met middelpunt S en straal gelijk aan R . sin w.(zie figuur 7)

figuur 7  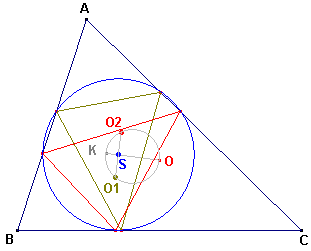bromile7 Opmerkingen
[1]
Dat de voetpuntsdriehoeken van de punten van Brocard dezelfde omcirkel hebben, blijkt ook uit het feit, dat de punten van Brocard isogonaal verwant zijn (Stelling 8.5 en 8.6 op de pagina "De punten van Brocard"); immers isogonale punten hebben dezelfde omcirkel (zie hiervoor ook  Stelling 3 op de pagina "Isogonale punten").
[2]
Het blijkt ook uit het feit, dat de voetpunten op de tweede cirkel van Lemoine liggen (zie de pagina "Tucker-cirkels").
[einde Opmerkingen en einde Gevolg]

begin pagina
[bromile.htm] laatste wijziging op: 06-07-2002