Tucker-cirkels

Overzicht  ][  Isogonalen  |   Koordenvierhoek  |  Meetkunde

0. Overzicht terug

  1. Inleiding
  2. Parallel en antiparallel, Tucker-zeshoek cabrisignal
         Stelling 1
  3. Tucker-cirkel cabrisignal
         Stelling 2
         Stelling 3
  4. Lemoine-cirkels zijn Tucker-cirkels cabrisignal
         Stelling 4
  5. De Taylor-cirkel cabrisignal
         Stelling 5
  6. Cirkel van Adams cabrisignal
         Stelling 6
  7. Referenties
  8. Download

1. Inleiding terug
Kennis vooraf:

-  het begrip antiparallel; zie hiervoor de pagina's "Isogonale verwantschap" en het Cabri-werkblad "Parallel en antiparallel";
- theorie der koordenvierhoeken; zie hiervoor de pagina "Koordenvierhoeken".

We kunnen in een driehoek op twee manieren een met die driehoek gelijkvormige driehoek construeren die tevens een hoek met die driehoek gemeenschappelijk heeft.
Zie hiervoor figuur 1.

figuur 1a figuur 1b
ptuck1b ptuck1b
parallellen antiparallellen

We zullen de combinatie van deze eigenschappen in de volgende paragrafen aan een nader onderzoek onderwerpen.

2. Parallel en antiparallel, Tucker-zeshoek terug

figuur 2 ptuck2 In figuur 2 zijn de punten S1, S2, S3 willekeurig gekozen op de zijden van de driehoek.
Door S1: S1P' antiparallel met BC; S1Q parallel met AC.
Door S2: S2R' antiparallel met AC; S2P parallel met AB.
Door S3: S3Q' antiparallel met AB; S3R parallel met BC.

Vraag
Wat gebeurt er nu als we S2 en S3 zo verplaatsen, dat P met P' en tegelijk ook Q met Q' samenvalt?
We verplaatsen S1 dus vooralsnog niet.

|§| Klik hier Animatie om deze vraag te beantwoorden met behulp van een animatie met CabriJava.

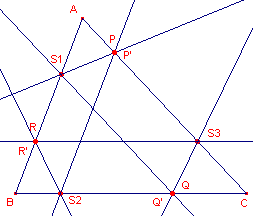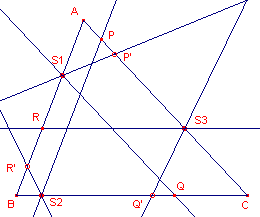
figuur 3 ptuck3 We zien dat dan ook R met R' samenvalt.
We kunnen de zeshoek S1PS2RS3Q dan volledige doorlopen.
De figuur "sluit" dus na Q weer in S1.

Vraag
Is dit voor elke ligging van S1 het geval.

|§| Klik ook nu weer op Animatie voor een onderzoek met CabriJava.

Definitie
Een (niet noodzakelijk convexe) zeshoek, waarvan de hoekpunten twee aan twee op de zijden van een driehoek liggen en waarvan de zijden afwisselend parallel en antiparallel zijn met de zijden van die driehoek, heet Tucker-zeshoek (zie figuur 4a).
De Tucker-zeshoek is genoemd naar Robert Tucker, die deze eigenschap in 1883 vermeldde.

We kunnen nu formuleren:

Stelling 1 terug
Elk punt van een zijde van een driehoek bepaalt een Tucker-zeshoek.

Bewijs: zie figuur 4a en figuur 4b.

figuur 4a figuur 4b
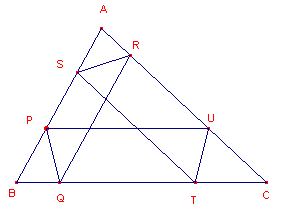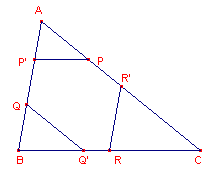
ptuck4 ptuck4b We hebben in het laatste onderzoek gezien, dat de antiparallelle zijden van de zeshoek aan elkaar gelijk zijn (in de hoekpunten van de driehoek hebben we dus congruente driehoekjes).
We zullen dat eerst bewijzen.
We bewijzen dat PQ = RS.
In figuur 4b zien we dat de hoeken bij P, Q, S en V van wege de (anti)parallelliteit van de lijnstukken gelijk zijn aan hoek C.
Vierhoek PQRS is een trapezium met gelijke basishoeken. Dus PQ = RS.

We passen nu het "Tucker-proces" als volgt toe: PQ/a/AC, QR//AB, RS/a/BC, ST//AC en TU/a/AB.
We verbinden vervolgens U en P, en bewijzen dat UP//BC. Zie verder figuur 4c.

figuur 4c 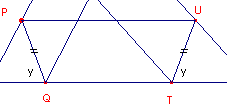ptuck4c Nu is in vierhoek PQTU hoek PQT gelijk aan UTQ, terwijl PQ gelijk is aan UT.
Hieruit volgt dan eenvoudig, dat UP//BC. ¨ 

3. Tucker-cirkel terug
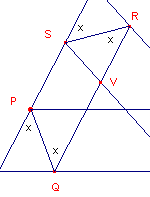
Een Tucker-zeshoek heeft echter nog een bijzondere eigenschap.

|§| Klik hier Animatie om deze eigenschap te bekijken met CabriJava.

We zullen nu bewijzen:

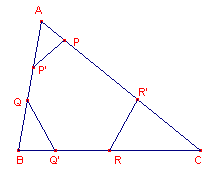
Stelling 2 terug
De hoekpunten van een Tucker-zeshoek liggen op een cirkel.

Bewijs: zie figuur 5.

figuur 5 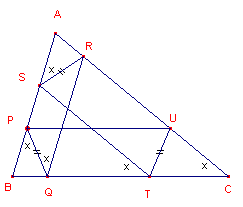ptuck5 PQRS is een gelijkbenig trapezium en dus een koordenvierhoek.
De buitenhoek van vierhoek PQTS bij S is gelijk aan de binnenhoek bij T (beide zijn gelijk aan hoek C van de driehoek).
Ook PQTS is dus een koordenvierhoek.
Deze koordenvierhoeken hebben als omgeschreven cirkel die van driehoek PQS.
De punten P, Q, R, S, T zijn dus conclyclisch.
Maar ook vierhoek PQTU is een koordenvierhoek (gelijkbeing trapezium). Ook U ligt dus op deze cirkel. ¨ 
.
Definitie
De omgeschreven cirkel van een Tucker-zeshoek heet Tucker-cirkel.

Elk punt op een zijde van een driehoek bepaalt een Tucker-zeshoek, dus ook een Tucker-cirkel.
We hebben dus een verzameling middelpunten van Tucker-cirkels.

Een ontaarde Tucker-cirkel kunnen we vinden als we figuur 6 beschouwen.

figuur 6 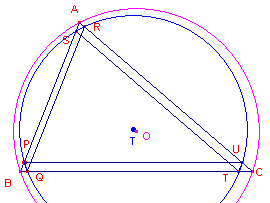ptuck6 Wat gebeurt er met de Tucker-cirkel als P (op AB) naar het punt B nadert?
Dan nadert Q ook naar B, terwijl de punten R en S naar A en de punten T en U naar C naderen.
In dit geval nadert de Tucker-cirkel dus tot de omcirkel van driehoek ABC.
Het middelpunt T van de Tucker-cirkel nadert dan tot het middelpunt O van de omcirkel.

Vraag
Ligt het punt O op de gezochte verzameling?

Conclusie
We kunnen de omcirkel van een driehoek beschouwen als een Tucker-cirkel waarbij de bijbehorende hoekpunten van de Tucker-zeshoek samenvallen met de hoekpunten van de driehoek.

|§| Klik hier Animatie om de gehele verzameling Tucker-middelpunten te onderzoeken.

Dit onderzoek leidt dan tot de volgende stelling:

Stelling 3 terug
De middelpunten van Tucker-cirkels liggen op de lijn KO, waarbij K het punt van de Lemoine is en O het omcentrum van de driehoek.

Bewijs: zie figuur 7.

figuur 7 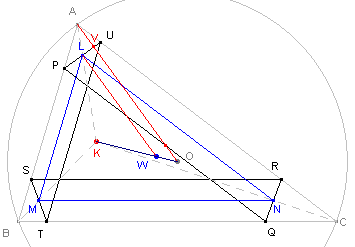ptuck7 De lijnen door de middens van de gelijke lijnstukken PU, ST en QR zijn symmedianen (zie hiervoor de pagina "Isogonale verwantschap", Stelling 5).
Ze gaan dus door één punt, K, het punt van Lemoine.
PUTS is een gelijkbenig trapezium. De lijn LM is daarin middenparallel; LM // AB.
Driehoek ABC is nu direct-gelijkvormig (homothetisch) met driehoek LMN; het centrum is het punt K en de factor zij m.
De omcirkel van driehoek ABC gaat daarbij over in de omcirkel van driehoek LMN.
Zij W het centrum van deze cirkel.
Het punt W ligt dus op KO!

We bekijken nu de lijnen LW en AO (AO snijdt PU in V).

In driehoek AOB is ÐAOB = 2g. Dus, ÐOAB = ½(180º-2g) = 90º-g.
Maar ook ÐAPU (in driehoek PAU) is gelijk aan g (PU /a/ BC).
Zodat in driehoek APV: ÐV = 90º.

figuur 8 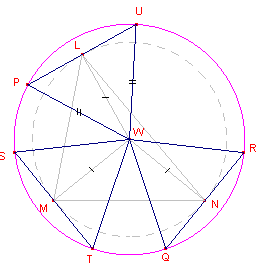ptuck8 Maar dan is ook hoek PLW = 90º, immers LW en AO zijn evenwijdig vanwege de homothetie met centrum K.
Met andere woorden: WL ^ PU, waaruit volgt, dat WP = WU.
Maar ook PU = ST = QR, terwijl L, M en N op een cirkel liggen.
Hieruit volgt eenvoudig, dat W het middelpunt is van de Tucker-cirkel PQRTSU.

Het middelpunt (W) van deze Tucker-cirkel ligt dus op KO. ¨ 

4. Lemoine-cirkels zijn Tucker-cirkels terug
Naast de omgeschreven cirkel van een driehoek (zie de Conclusie in paragraaf 3) zijn er nog twee bijzondere Tucker-cirkels, de zogenoemde cirkels van Lemoine.
De eerste cirkel van Lemoine krijgen we als de zijden van de Tucker-zeshoek die parallel zijn met de zijden van de driehoek, door het punt van Lemoine gaan (zie figuur 9a).
De tweede cirkel van Lemoine vinden we als de zijden van de Tucker-zeshoek die antiparallel zijn met de zijden van de driehoek, door het punt van Lemoine gaan (zie figuur 9b).
De tweede Lemoine-cirkel wordt ook wel aangeduid met cosinus-cirkel (zie Opmerking na het Bewijs [2] van Stelling 4).

figuur 9a       figuur 9b
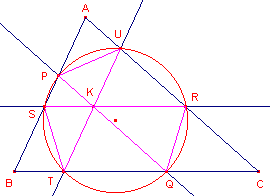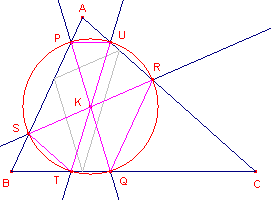ptucklem2 ptucklem1
eerste cirkel van Lemoine -  parallel tweede cirkel van Lemoine - antiparallel

We bewijzen:

Stelling 4 terug
De beide Lemoine-cirkels zijn Tucker-cirkels.

Bewijs:
[2]
Eerst het bewijs voor de tweede cirkel. Dat bewijs is het meest elementair (zie figuur 9b).
De lijn AK deelt de zijde van de voetpuntsdriehoek van ABC midden door. K is dus het midden van SR:
KS = KR. Evenzo ook: KP=KQ en KT=KU.
In driehoek KUR is:
ÐU = ÐB (van driehoek ABC), immers UT /a/ AB
ÐR = ÐB (van driehhoek ABC), immers SR /a/ BC.
Dus KU = KR.
Waaruit eenvoudig volgt dat KP=KQ=KR=KS=KT=KU. Dus K is middelpunt van de cirkel PQRSTU.
Gevolg:
Kijkend naar driehoek KST. Hierin is ÐT gelijk aan ÐB. ÐUTC = ÐA, zodat ÐBTS = ÐC.
Dus: ST // AC.
De andere zijden van de zeshoek zijn dus evenwijdig aan de zijden van driehoek ABC.
PQRSTU is dus een Tucker-zeshoek.  ¨ 

Opmerking
In driehoek KUR is, zoals opgemerkt, ÐU = ÐB.
Voor UR hebben we dan UR = 2r.cosB (waarin r de straal is van de tweede Lemoine-cirkel).
Zo vinden we ook PS = 2r.cosC en TQ = 2r.cosA, zodat voor de koorden die de tweede Lemoine-cirkel afsnijdt op de zijden van de driehoek, geldt:
   TQ : UR : PS = cosA : cosB : cosC
Vandaar ook de naam cosinuscirkel voor de tweede Lemoine-cirkel.
[einde Opmerking]

[1]
Vervolgens het bewijs voor de eerste cirkel.
We zullen aantonen, dat de niet-evenwijdige zijden van de zeshoek PQRSTU antiparallel zijn met de zijden van driehoek ABC.

figuur 9c 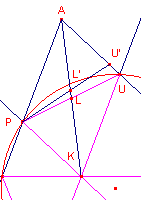ptucklem3 APKU is een parallellogram. AK snijdt PU dus in het midden L.
Stel PU is niet antiparallel met BC.
Dan kunnen we PU' antiparallel tekenen met BC.
Maar dan is ook L' het midden van PU' (eigenschap van de symmediaan AK).
In driehoek PUU' is dus LL' de lijn die de middens van de zijden PU en PU' verbindt.
Dus: LL' // UU'. Maar dit is onmogelijk.
Dus is PU wel antiparallel met BC.
Hetzelfde geldt voor de andere niet-evenwijdige zijden van de zeshoek.
PQRSTU is dus een Tucker-zeshoek.  ¨ 

Gevolg

figuur 9d 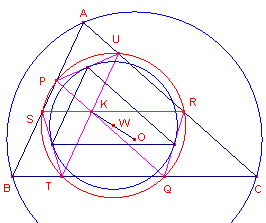ptucklem4 De gelijkvormigheidsfactor m, genoemd in het bewijs van Stelling 3, is in dit geval gelijk aan ½.
Het middelpunt W van de eerste Lemoine-cirkel is dus het midden van het lijnstuk KO, waarbij O het omcentrum van driehoek ABC is.

Klik hier Animatie voor een animatie waarmee de ligging van de middelpunten van de beide Lemoine-cirkels kan worden bekeken.

Opmerking
Het midden van KO is het middelpunt van de zogenoemde Brocard-cirkel (zie de pagina "Brocard, Lemoine, Miquel").
Zie verder ook de paragraaf Referenties.
[einde Opmerking]

[einde Gevolg]

5. De Taylor-cirkel terug
We hebben in Stelling 1 gezien, dat elk punt van een zijde van een driehoek een Tucker-zeshoek, en dus ook een Tucker-cirkel bepaalt.
Het aantal "bijzondere" Tucker-cirkels is echter niet groot.
We bekijken in deze paragraaf de zogenoemde Taylor-cirkel van een driehoek.

Klik hier Animatie voor een animatie met CabriJava.

figuur 10 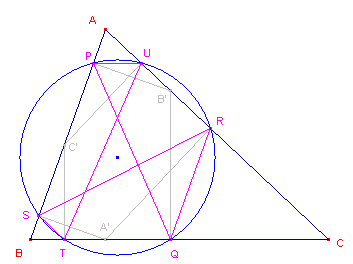ptucktay1 In figuur 10 zijn de punten A', B', C' de voetpunten van de hoogtelijnen uit A, B, C.
Uit deze punten zijn loodlijnen neergelaten op de zijden van de driehoek.
De voetpunten van deze loodlijnen vormen een Tucker-zeshoek en liggen dus op een Tucker-cirkel.
Deze Tucker-cirkel heet de Taylor-cirkel van de driehoek. Het middelpunt van de cirkel heet Taylor-punt van de driehoek.

We bewijzen nu:

Stelling 5 terug
De Taylor-cirkel van een driehoek is een Tucker-cirkel.

Bewijs: zie eerst figuur 11.

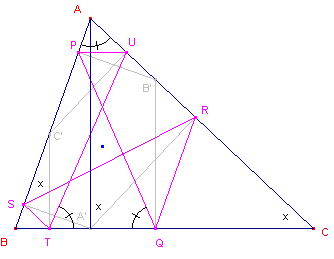figuur 11 ptucktay2 We bewijzen allereerst dat de lijnen PQ, RS en TU antiparallel zijn met de zijden.
In de rechthoekige driehoek AA'C is ÐAA'R = ÐC, immers A'R is hoogtelijn in die driehoek.
Vierhoek ASA'R is een koordenvierhoek (twee overstaande rechte hoeken). Dus:
ÐASR = ÐAA'R (omtrekshoeken op gelijke bogen).
Dus:
RS /a/ BC.
Evenzo zijn ook de andere genoemde zijden van de zeshoek antiparallel met de zijden van de driehoek.

Hieruit volgt in ieder geval dat ÐUTQ = ÐPQT = ÐA.

We zullen nu aantonen, dat PQ = TU. Immers, is dit het geval, dan is PUQT een gelijkbenig trapezium.
Zie hiervoor figuur 12.

figuur 12 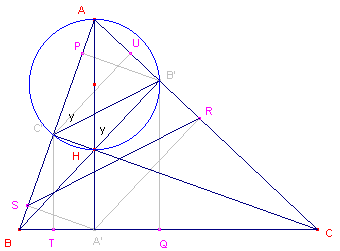ptucktay3 We berekenen de lengte van RS (de derde van de drie antiparallelle zijden van de zeshoek).
B' en C' zijn voetpunten van hoogtelijnen. Dus:
B'C' /a/ BC, zodat
   B'C' // RS.
In driehoek ARS is dan
   RS : B'C' = AS : AC' ......(1)
Maar ook, in driehoek AA'S:
   AS : AC' = A'S : HC' = AA' : AH ......(2)
Uit (1) en (2) volgt dan:
   RS : B'C' = AA' : AH, zodat

   RS = AA' . (B'C'/AH) ......(3)
Nu is AC'HB' een koordenvierhoek, zodat ÐAC'B' = ÐAHB' (in figuur 12 aangegeven met y).
In driehoek AB'C' hebben we dan: B'C'/sin A = AB'/sin y.
Maar in driehoek AHB' is sin y =AB' / AH, waaruit we dus vinden:
   B'C'/sin A = AH ......(4)
(4) samen met (3) geeft dan:
   RS = AA' . sin A ......(5)
Zij V nu de oppervlakte van driehoek ABC. Dan is V = ½AA' . BC, zodat
   AA' = 2V/a (a is de lengte van BC).
Dus, uit (5):
   RS = 2V sinA/a
Volgens de sinusregel is sinA/a = 1/(2R), waarin R de straal van de omcirkel is van driehoek ABC.
Zodat uiteindelijk:
   RS = V/R
Dus ook PQ = V/R en UT = V/R, zodat PQ = UT.
Waarmee Stelling 5 geheel bewezen is.  ¨ 

Opmerking
De cirkel is genoemd naar H.M.Taylor (1842-1927) die erover publiceerde in 1882. Eerder zijn er echter ook publicaties over deze cirkel geweest, oa. in 1879 door Catalan (Eugène Charles Catalan, 1814-1894, België).
[einde Opmerking]

6. Cirkel van Adams terug

Klik hier Animatie voor een animatie met CabriJava.

figuur 13 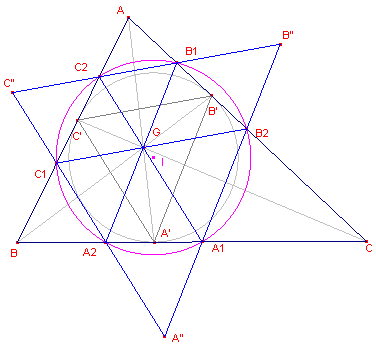ptuckad1 In figuur 13:
- G is het punt van Gergonne;  dit is het snijpunt van de verbindingslijnstukken van de hoekpunten naar de raakpunten van de incirkel met de zijden;
- A'B'C' is de Gergonne-driehoek van driehoek ABC;
- B2C1 // B'C', C1A2 // C'A', A1B2 // A'B'; alle lijnen gaan door G;
- de lijnen B2C1, C1A2 en A1B2 bepalen de driehoek A"B"C".

Klik hier voor een eigenschap van het Gergonne-punt en de Gergonne-driehoek.
Deze eigenschap gebruiken we bij het bewijs van Stelling 6.2:
.
Stelling 6 terug
[1] De punten A1, A2, B1, B2, C1, C2 zijn concyclisch met middelpunt I (incentrum van driehoek ABC).
De cirkel heet de cirkel van Adams van de driehoek (naar Carl Adams, 1811-1849, Zwitserland).
[2] G is symmediaanpunt van driehoek A"B"C".
[3] De Adams-cirkel van driehoek ABC is de eerste Lemoine-cirkel van A"B"C".

Opmerking
Adams publiceerde over de naar hem genoemde cirkel in zijn boek "Die Lehre von den Transversalen in ihrer Anwendung auf die Planimetrie. Eine Erweiterung der euklidischen Geometrie" (Steiner, Winterthur).
[einde Opmerking]

Bewijs: zie figuur 14a.

figuur 14a 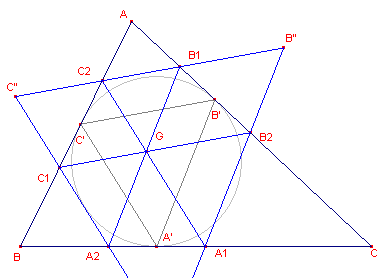ptuckad2 [6.1]
Bekijk de vierhoek A1A2B1B2.
CA' = CB' (gelijke raaklijnstukken uit C aan de incirkel).
Driehoek CA'B' is dus gelijkbenig.
A2B1 // A'B'. Zodat ook driehoek CA2B1 gelijkbenig is.
Hieruit volgt dat A'A2 = B'B1
(en dus op dezelfde manier B'B2=C'C1 en C'C2=A'A1).
figuur 14b 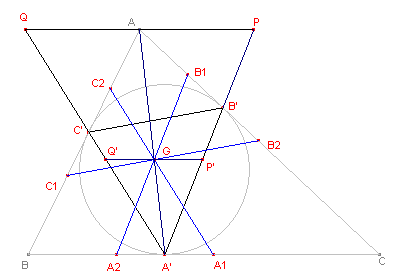ptuckad3 Zie nu verder figuur 14b.
We tekenen door A een lijn evenwijdig met BC.
De lijnen AB' en A;C' snijden deze lijn in opvolgend P en Q.
Nu zijn de driehoeken APB' en AQC' gelijkbenig (beide met top A).
Omdat AC'=AB' geldt AP=AQ.
De lijn A"A is dus zwaartelijn van driehoek A'PQ.
Bij de vermenigvuldiging met centrum A' en factor A'G/A'A gaat het lijnstuk PQ over in een lijnstuk P'Q' (door G).
Nu zijn A'A2GP' en A'A1GQ' parallellogrammen, waaruit volgt dat
figuur 14c 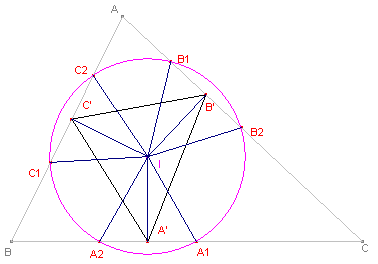ptuckad4 A'A2 = GP' = GQ' = A'A1
(analoog voor de andere lijnstukjes).
Dus A1A2 = B1B2, waardoor driehoek CA1B2 gelijkbenig is.
De lijn A1B2 is dus evenwijdig met A2B1 (wordt gebruikt bij het bewijs van Stelling 6.2).

Zie verder figuur 14c.
Er onstaan nu 6 rechthoekige driehoekjes A'A1I, A'A2I, ... die alle congruent zijn.
Daaruit volgt dan
IA1 = IA2 = IB1 = IB2 = IC1 = IC2
waarmee Stelling 6.1 bewezen is.

[6.2]
Uit het eerste deel van het bewijs weten we: A1B2 // A2B1 (en ook A2C1//A1C2, B1C2//B2C1).
We bekijken nu de vermenigvuldiging met centrum G en factor 2.
Hierdoor gaan de driehoek A'B'C' over in driehoek A"B"C".
G is het symmediaanpunt van driehoek A'B'C' (zie hiervoor de pagina "Gergonnepunt en -driehoek"); dus G is ok het symmediaanpunt van A"B"C".

[6.3]
De lijnen A2B1, A1C2 en B2C1 gaan door het symmediaanpunt van A"B"C' en zijn evenwijdig met de zijden daarvan.
De punten A1, A2, B1, B2, C1, C2 vormen dus de eerste Lemoine-cirkel van driehoek A"B"C" (zie Stelling 4).  ¨ 

7. Referenties terug

[1]  Lemoine-cirkels
De beide Lemoine-cirkels komen ook aan de orde op het Cabri-werkblad "Parallel en antiparallel".
Er bestaat een verband tussen de eerste cirkel van Lemoine, de beide punten van Brocard en een Miquel-punt.
Zie voor dit verband de pagina "Verband tussen de punten van Brocard, ...".
[2] Isogonale verwantschap, antiparallel
Een algemene inleiding hiervan is te vinden op de pagina "Isogonale verwantschap".
Op die pagina wordt eveneens ingegaan op het punt van Lemoine.
[3] Taylor-cirkel
Zie voor enkele andere eigenschappen van de Taylor-cirkel de betreffende pagina op website van Wolfram Research.
[4] Brocard-driehoek
Op de pagina "Brocard-driehoeken" wordt het Gevolg van Stelling 4 gebruikt om een eigenschap van de Brocard-cirkel te bewijzen.

8. Download terug
De Cabri-figuren die gebruikt zijn bij de animaties op deze pagina kunnen via deze website in één bestand worden gedownload.
Klik hier om het downloaden te starten [ZIP-bestand, ca. 6Kb].

begin pagina
[tucker.htm] laatste wijziging op: 27-12-04