Bijzondere gelijkvormige driehoeken bij een driehoek

Overzicht ][ Brocard-driehoeken | Neuberg-cirkels | Meetkunde

Overzicht

Bijzondere gelijkvormige driehoeken
Kiepert en Brocard
Neuberg-driehoek

1. Bijzondere gelijkvormige driehoeken

Stelling 1
Als de driehoeken PBC, QCA, RAB direct gelijkvormig zijn en "op dezelfde manier gelegen" zijn tov. ABC, dan valt het zwaartepunt van PQR samen met dat van ABC.

Opmerkingen
[1]
"Op dezelfde manier gelegen" kan worden opgevat als:
Twee van de drie driehoeken zijn uit de derde ontstaan door een draaivermenigvuldiging in tegengestelde richtingen.
[2]
Stelling 1 is dezelfde als Stelling 4b op de pagina "Brocard-driehoeken".
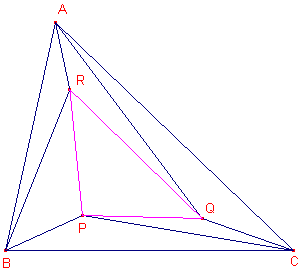[einde Opmerkingen]

Klik hier voor een CabriJavapplet bij Stelling 1.

Bewijs:

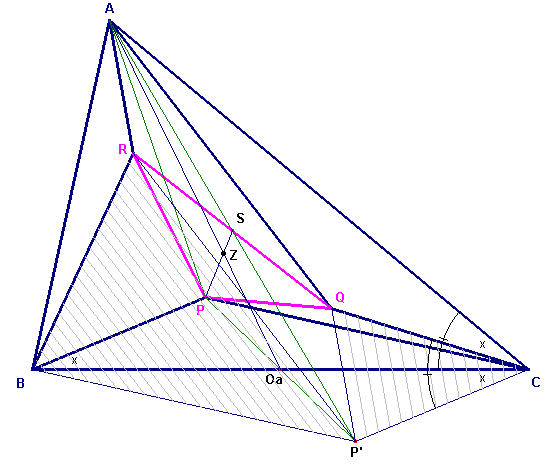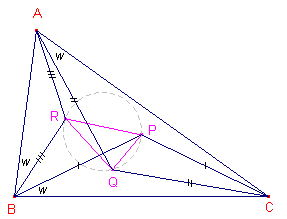
PBC ~ QCA ~ RAB
waaruit:
RB : QA = AB : AC of RB = QA ^. AB/AC ......(1)

Oa is het midden van BC. P' is het speigelbeeld van P in Oa.
PBP'C is een parallellogram, zodat PBC = P'BC.
Nu is P'CQ = C.
Verder is
QC : P'C = QC : BP = AC : BC, zodat
QP'C ~ ABC
Evenzo:
RBP' ~ ABC
Uit deze gelijkvormheden volgt nu:
RP' : QC = RB : QP' ......(2)
QP' : AB = QC : AC ......(3)
Deling van (2) en (3) geeft dan:
RB = RP' . AB/AC ......(4)
Uit (1) en (4) volgt dan QA = RP' ......(5)
Evenzo kunnen we bewijzen: AR = QP' ......(6)
Uit (5) en (6) volgt dan dat ARP'Q een parallellogram is.
Zij S het snijpunt van de diagonalen (S is het midden van AP').

AOa en PS zijn zwaartelijnen (met zwaartepunt Z) in driehoek APP'. Dus PZ : ZS = 2 :1. Hieruit volgt dat Z zwaartepunt is van PQR.
Z is eveneens het zwaartepunt van ABC (immers Z op AOa met AZ : ZOa = 2 : 1, in APP'). ¨

2. Kiepert en Brocard
Zie in dit verband ook de Stelling van Kiepert op de pagina "Het probleem van Lemoine":
Er geldt:

Stelling 2
Worden gelijkvormige gelijkbenige driehoeken ABC', BCA' en CAB' op de zijden van driehoek ABC beschreven, dan zijn AA', BB', CC' concurrent.
(Ludwig Kiepert, 1846-1934, Duitsland)

Opmerking
Het bewijs van deze stelling is niet elementair.
[einde Opmerking]

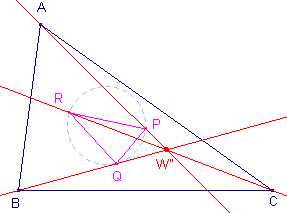Uit de Stelling van Kiepert volgt echter eenvoudig de perspectiviteit (in het punt W") van een driehoek (ABC) en de daarbij behorende 1e Brocard-driehoek (PQR).
W" is het 3e Brocard-punt van de driehoek (zie de pagina Brocard-driehoeken).

Gevolg van Stelling 1
Een driehoek en de 1e Brocard-driehoek van die driehoek hebben hetzelfde zwaartepunt.

Bewijs:
De gemeenschappelijke Brocard-hoek w doet gelijkbenige, gelijkvormige driehoeken PBC, QCA en RAB ontstaan. ¨
Zie hiervoor verder eveneens de pagina "Brocard-driehoeken".

3. Neuberg-driehoek
Op de pagina "Neuberg-cirkels" wordt de Neuberg-driehoek van een driehoek gedefinieerd.
Ook hierbij geldt

Stelling 3
Een driehoek en diens Neuberg-driehoek hebben hetzelfde zwaartepunt.

Bewijs:

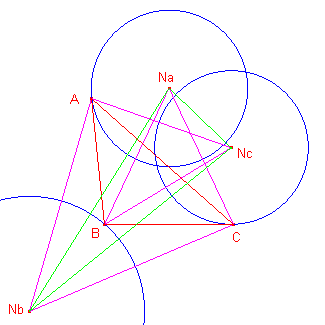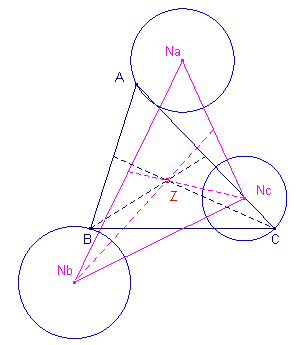
In de rechter figuur zijn de driehoeken N_aBC, N_bCA, N_cAB gelijkbenig.
De punten Na, Nb, Nc zijn de middelpunten van de Neuberg-cirkels (welke gelegen zijn op de middelloodlijnen van de zijden van ABC, eea. volgend uit de constructie ervan).
De hoeken bij Na, Nb, Nc in die driehoeken zijn gelijk aan 2w (waarbij w de Brocard-hoek is van driehoek ABC).
De driehoeken voldoen daardoor aan Stelling 1.
De Neuberg-driehoek heeft dus ook het punt Z (het zwaartepunt van ABC) als zwaartepunt. ¨

Opmerking
Stelling 3 is dezelfde als Stelling 9 op de pagina "Neuberg-cirkels".
[einde Opmerking]

[similartriangles.htm] laatste wijziging op: 12-08-02