Probleem van Lemoine en de stelling van Kiepert
- Het probleem en een oplossing
- Isogonalen en hun gevolg
- Hyperbool van Kiepert

- Bijzonderheden van de hyperbool
4.1. Hoogtepunt
4.2. Zwaartepunt
4.3. Punt van Fermat
4.4. Tweede punt van Fermat
4.5. Napoleon-punten
4.6. Punten van Vecten
4.7. Orthogonaal - De asymptoten van de hyperbool
- Referenties
- Download
1. Het probleem
en een oplossing ![]()
Probleem van Lemoine
Het volgende probleem is door Lemoine (Emile Lemoine, 1840-1912, Frankrijk) vermeld:
| "Construire un triangle, connaissant les sommets des triangles equilatéraux construits sur les cotes" |
(Frans: equilatéral = Nederlands: gelijkZIJDIG)
Iets ruimer geformuleerd:
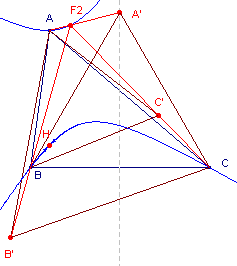
| Op de zijden van een driehoek ABC zijn gelijkBENIGE
driehoeken ABC', BCA' en CAB' geconstrueerd (zie figuur 1). Gevraagd wordt driehoek ABC te construeren als de punten A', B', C' gegeven zijn. |
| . |
| figuur 1 | 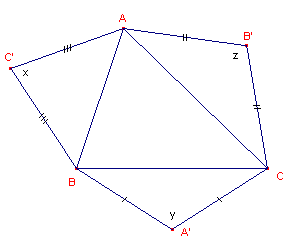 |
We geven hierbij direct maar een oplossing. De tophoeken van de gelijkbenige driehoeken zijn x, y, en z. Onder de aanname dat het probleem is opgelost, passen we de volgende rotaties toe: R1(C', -x), R2(A', -y), R3(B', -z) Het minteken geeft hierbij aan dat we de negatieve rotatierichting kiezen. In het algemeen is R3R2R1 een rotatie over de hoek x+y+z (zie de pagina "Rotaties"). Voor een willekeurig punt X in het vlak geldt dan (zie figuur 2): R3R2R1(X) = R3R2(X1) = R3(X2) = X3. |
| figuur 2 | 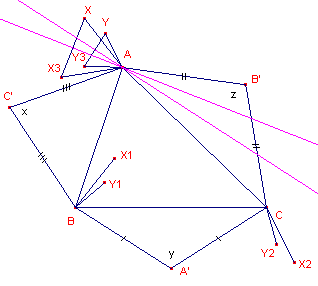 |
R3R2R1(AX)
= R3R2(BX1)
= R3(CX2) = AX3 Hierbij is AX = BX1 = CX2 = AX3. A ligt dus op de middelloodlijn van XX3. Voor een tweede willekeurig punt Y hebben we op dezelfde manier: R3R2R1(AY) = AY3 Het punt A is dan het snijpunt van de middelloodlijnen van XX3 en YY3. De punten B en C kunnen daarna geconstrueerd worden als R1(A) en R2(B). Waarmee ook het probleem van Lemoine is opgelost.¨ |
Opmerking
Het probleem heeft een unieke oplossing als de beide middelloodlijnen elkaar snijden.
Zijn ze evenwijdig dan is er geen oplossing; in dit geval is x + y + z gelijk aan (een
veelvoud van) 360º.
Als x + y + z = k·360º kan R3R2R1
ook de identieke afbeelding zijn. In dat geval zijn er oneindig veel oplossingen (elk punt
van het vlak kan dan als het punt A gekozen worden).
[einde Opmerking]
__________
Referentie
Zie [4].
¯¯¯¯¯¯¯¯¯¯
De verkregen figuur heeft (met een kleine beperking) nog een andere eigenschap (zie figuur 3), geformuleerd in Stelling 1 (genoemd
naar
Ludwig
Kiepert, 1846-1934, Duitsland).
| figuur 3 | 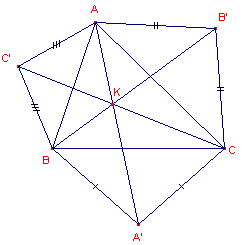 |
We zullen deze eigenschap in paragraaf 2 in een ander kader plaatsen (Stelling 1 volgt uit de daar vermelde Stelling 2). Opmerking |
2. Isogonalen en
hun gevolg ![]()
We geven eerst een definitie die ook elders (zie de pagina "Isogonale verwantschap, ...") op deze website staat, zij
het in een iets andere vorm.
| Definitie Twee hoektransversalen door hetzelfde hoekpunt van een driehoek zijn isogonaal (verwant) als ze elkaars beeld zijn bij spiegeling in de bissectrice van dat hoekpunt. |
We bekijken nu de volgende situatie:
| figuur 4 | 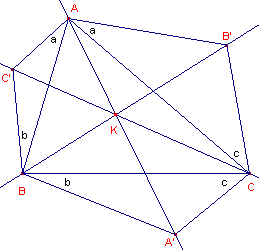 |
Stelling 1 volgt nu onmiddellijk uit Stelling 2 voor a = b = c = j, waarbij j de basishoek is van de in Stelling 1 genoemde gelijkbenige (gelijkvormige) driehoeken. Klik hier voor het bewijs van Stelling 2 (PDF-bestand; ca. 28 Kb) |
3. Hyperbool van
Kiepert ![]()
We kunnen de situatie als in Stelling 1 nu als volgt construeren:
- Kies A' willekeurig op de middelloodlijn van BC
- Spiegel de lijnen A'B en A'C opvolgend in de bissectrices van hoek B en van hoek C
- Bepaal de punten B' en C' op de middelloodlijnen van opvolgend AB en CA.
- Teken de lijnen AB' en AC' (zie figuur 5).
| figuur 5 | 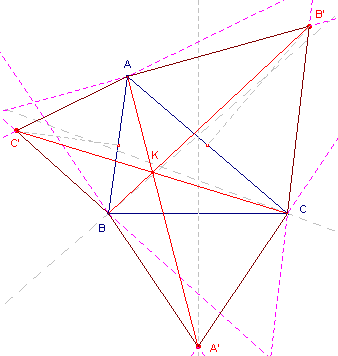 |
figuur 6 | 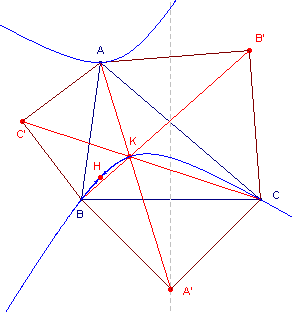 |
Het punt A' kan vrij gekozen worden op de middelloodlijn van BC.
De ligging van het punt K wordt bepaald door de ligging van A'.
In figuur 6 is de meetkundige plaats getekend van het punt K als A' de
middelloodlijn van BC doorloopt.
Deze meetkundige plaats is een hyperbool die gaat door de punten A, B
en C.
Deze hyperbool heet hyperbool van Kiepert van driehoek ABC (naar
Ludwig Kiepert,
1846-1934, Duitsland).
Klik hier ![]() voor een CabriJavapplet
bij deze constructie.
voor een CabriJavapplet
bij deze constructie.
Opmerkingen
Zie ook Stelling 5 op de pagina "Euler-cirkels".
Zie ook de pagina "Orthogonale hyperbool en
driehoek"
[einde Opmerking]
4. Bijzonderheden
van de hyperbool ![]()
Op de hyperbool van Kiepert liggen een aantal bijzondere punten.
We geven de grootte van de basishoeken van de gelijkvormige, gelijkbenige driehoeken op de
zijden telkens aan met j, waarbij -p/2
£ j £ p/2.
| 4.1. Hoogtepunt | ||
| figuur 7 | 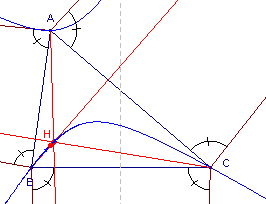 |
j = p/2 of j = - p/2 In figuur 7 is de situatie weergegeven voor j = p/2 - e . Bij de bepaling van de Kiepert-hyperbool (met Cabri in de figuur hiernaast) is H het limiet-punt als A'® L¥ waarbij L¥ het oneigenlijk punt is van de middelloodlijn van BC. |
| 4.2. Zwaartepunt |
||
| figuur 8 | 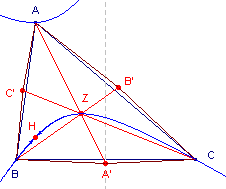 |
j = 0 In figuur 8 is de situatie weergegeven voor j = e . |
| 4.3. Punt van Fermat (uitwendig Fermat-punt of 1e Fermat-punt) |
||
| figuur 9 | 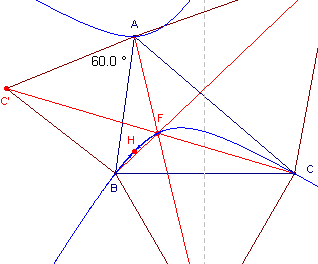 |
j = p/3 In figuur 8 is de situatie weergegeven voor j = p/3 . Zie hiervoor het Cabri-werkblad "Het punt van Fermat". |
| 4.4. Tweede punt van Fermat (inwendig Fermat-punt of 2e Fermat-punt) |
||
| figuur 10 |
|
j = -p/3
Het Tweede punt van Fermat wordt dus bepaald door de gelijkzijdige driehoeken inwendig op de zijden van driehoek ABC te construeren. Zie ook de pagina "Lester-cirkel". |
| 4.5. Napoleon-punten |
||
| figuur 11a | 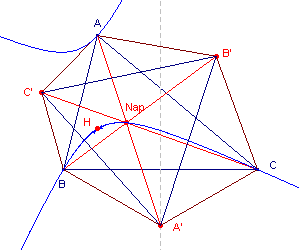 |
Eerste Napoleon-punt: j = p/6 (uitwendig) Tweede Napoleon-punt: j = -p/6 (inwendig) In figuur 11a is alleen het 1e Napoleon-punt getekend.
Zie ook het Cabri-werkblad "Het punt van Fermat en de driehoek van Napoleon". |
| 4.6. Punten van Vecten |
||
| Eerste punt van Vecten: j = p/4 (uitwendig) Tweede punt van Vecten: j = -p/4 (inwendig) De punten van Vecten vinden we door (uit- cq. inwendig) vierkanten te construeren op de zijden van de driehoek. Zie ook de pagina "Figuur van Vecten". |
||
In [2] worden nog 10 andere punten genoemd die op de Kiepert-hyperbool liggen.
4.7. Orthogonaal
Doordat de hyperbool door het hoogtepunt van de driehoek gaat, is de Kiepert-hyperbool orthogonaal
(zie ook paragraaf 5).
Overigens, er kan bewezen worden:
| Stelling 3 Alle hyperbolen die gaan door de hoekpunten van een driehoek èn door het hoogtepunt van die driehoek, zijn orthogonaal. De verzameling van de middelpunten is de negenpuntscirkel. |
Zie ook de pagina "Probleem van Poncelet-Brianchon" en Stelling 5 op de pagina "Euler-cirkels".
5. De asymptoten
van de hyperbool van Kiepert ![]()
Zoals we in paragraaf 4 reeds zagen, liggen op de hyperbool van Kiepert
een aantal bijzondere punten.
Ook de asymptoten van de hyperbool zijn bijzondere lijnen (zie figuur 12).
| figuur 12 | 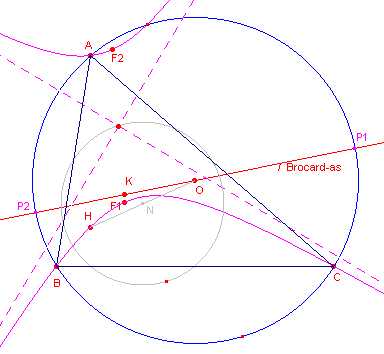 |
De lijn door het punt K van Lemoine (symmediaanpunt)
en het omcentrum O wordt de Brocard-as genoemd. De Brocard-as snijdt de omcirkel van de driehoek in de punten P1 en P2. Nu geldt: [1] [2] |
Opmerking
Ook uit het feit dat de punten P1 en P2
tegenpunten zijn op de omcirkel, volgt dat de Kiepert-hyperbool orthogonaal
is.
[einde Opmerking]
| [1] | H.S.M. COXETER, Introduction to Geometry, John Wiley & Sons, New York, 1961 | |
| [2] | C. KIMBERLING, Triangle Centers and Central Triangles, Utilitas Mathematica Publishing Inc., Winnipeg (Canada); Congressus Numerantium 129, 1998 | |
| [3] | Clark Kimberling's "Encyclopedia of Triangle Centers - ETC" - University of Evansville, USA | |
| [4] | I.M. YAGLOM, Geometric transformations, Vol. 1, pag. 37, Random House, New York, 1962 |
7. Download
De figuren gebruikt in de CabriJavapplets kunnen in een bestand via deze website worden
gedownload.
Klik hier om het downloaden te starten
(ZIP-bestand; ca 4kB).
Met dank aan FLOOR VAN LAMOEN voor zijn opmerkingen en aanvullingen.
[lemoine.htm] (04-07-2005) laatste wijziging op: 26-03-18