Rotaties

Overzicht  ][  Draaivermenigvuldiging | Meetkunde

Zie ook de pagina "Bewegingen".

0. Overzicht begin pagina

  1. Inleiding
  2. Som van twee rotaties
  3. Centrum van de som  cabrisignal
  4. Sylvester's rotator  cabrisignal
  1. Referenties

1. Inleiding begin pagina

Definitie
O is een vast punt van het vlak
Zijn A en A' twee punten in het vlak met OA = OA' en ÐAOA' = a, dan noemen we A' het rotatiebeeld van A bij een rotatie om O (met centrum O) over de hoek a.
Notatie: R(O, a)
De verzameling van alle beelden van de punten van een figuur F vormen een nieuwe figuur F' die rotatiebeeld van F heet.
.
Stelling 1
Zijn F en F' elkaars rotatiebeeld bij een rotatie met centrum O en hoek a, dan zijn overeenkomstige lijnstukken van deze figuren gelijk en maken een hoek a.

Bewijs:

figuur 1 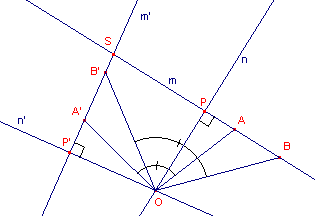rotatie1 In de figuur hiernaast is ÐAOB=ÐA'OB', immers ÐAOA'=ÐBOB'=a.
A' en B' zijn het beeld van A resp. B, zodat OA=OA' en OB=OB'.
Dus zijn de driehoeken AOB en A'OB' congruent (ZHZ), waaruit volgt, dat AB =A'B' (overeenkomstige lijnstukken).
m en m' zijn drager van opvolgend AB en A'B'.
n staat loodrecht op m, n' staat loodrecht op m'.
OAP en OA'P' zijn congruent (ZHH), waaruit volgt dat OP=OP' en ÐAOP=ÐA'OP'.
Uit dit laatste volgt dan ÐPOP' = a.

In koordenvierhoek OPSP' is een hoek bij S dus gelijk aan a.¨

Omgekeerd:

Stelling 2
Als met elk punt van een figuur F een punt van een andere figuur F' correspondeert en corresponderende lijnstukken van deze figuren gelijk zijn en een hoek a met elkaar maken, dan is F' het beeld van F bij een rotatie over a.

Bewijs:

figuur 2 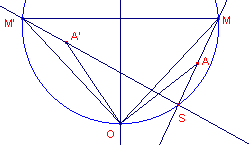rotatie2 Construeer een cirkel waarvan MM' een hoek a onderspant.
Zij O het snijpunt van de middelloodlijn van MM' en de cirkel zodanig, dat MOM' gelijk is aan a.
De rotatie R(O, a) beeldt nu M op M' af. Zijn A en A' twee corresponderende punten. We moeten nu aantonen, dat ÐAOA'=a.
In de driehoeken MAO en M'A'O hebben we:
(1) OM=OM' (door constructie);
(2) MA=MA' (gegeven);
(3) ÐOMA=ÐOM'A'

(3) volgt uit het feit, dat de punten M, M', S (als snijpunt van MA en M'A') en O concyclisch zijn.
De driehoeken MAO en M'A'O zijn dus congruent, zodat OA=OA' en verder ÐAOM=ÐA'OM'. Uit dit laatste volgt dan ook ÐAOA' = ÐMOM' = a.
Zodat een willekeurig punt A van F door R(O, a) op een overeenkomstig punt A' van F' wordt afgebeeld. Waaruit het gestelde volgt.¨

2. Som van twee rotaties begin pagina
We maken onderscheid tussen gemeenschappelijke centra en verschillende centra.

2.1. Gemeenschappelijke centra
Uit de definitie van rotatie volgt eenvoudig dat de som (zie Opmerking) van twee rotaties met gemeenschappelijk centrum O en hoeken a en b de rotatie R(O, a + b) is.

Opmerking
Onder de som verstaan we het na elkaar uitvoeren van twee rotaties R1 en R2.
Passen we eerst R1 toe op een punt X en vervolgens R2 op het beeld van X, dan schrijven we dit als
R2R1(X) of ook wel R2oR1(X), waarbij de operator "o" wordt uitgesproken als "na".
[einde Opmerking]

2.2. Verschillende centra
We gaan uit van de figuren F, F1 en F2 waarbij R1(F)=F1 en R2(F1)=F2 over respectievelijk de hoeken a en b.
Lijnstukken AB van F gaan door R1 over in gelijke lijnstukken A1B1 van F1 waarbij de hoek tussen AB en A1B1 gelijk is aan a.
Lijnstukken A1B1 van F1 gaan door R2 over in gelijke lijnstukken A2B2 van F2 waarbij de hoek tussen A1B1 en A2B2 gelijk is aan b.
De hoek tussen corresponderende lijnstukken AB en A2B2 van F en F2 is dus gelijk aan a+b, waarbij ook AB=A2B2.

[1] a+b = 360º
Nu is AB//A2B2.
In dit geval is er dus sprake van een translatie indien de som geen dekpunten heeft.
Zijn er wel dekpunten, dan is de som de identieke afbeelding.

[2] a+b ¹ 360º
Uit Stelling 2 volgt in dit geval, dat R2R1 een rotatie is over de hoek a+b.
Omdat een rotatie over een hoek a gelijk is aan een rotatie over de hoek 360º - a (tegengestelde richting) kunnen we algemeen formuleren:

Stelling 3
De som van twee rotaties is een translatie als de rotatiehoeken gelijk zijn maar tegengesteld en is een rotatie in andere gevallen.

3. Centrum van de som begin pagina
Zijn O1 en O2 de centra van de rotaties R1 en R2, met hoeken a en b, waarbij a+b ¹ 360º.
Voor O1 hebben we O1' = R2R1(O1), waarbij O1O1' = O1O2 en ÐO1O2O1' = b (zie figuur 3).
Voor een zeker punt A hebben we verder R2R1(A) = O2 met O1A=O1O2.

figuur 3 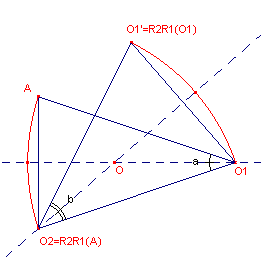rotatie3 Voor het centrum O van de rotatie R2R1 geldt dan:
- O op de middelloodlijn van O1O1'
- O op de middelloodlijn van AO2.
O is dus het snijpunt van beide middelloodlijnen.

Klik hier Animatie voor een CabriJavapplet ter illustratie.

Opmerking
Zie ook de pagina "Macro's voor figuren" waarop een macro voor de som van twee rotaties wordt besproken, gebaseerd op nevenstaande constructie.
[einde Opmerking]

Voor a + b =360° (of b =360° - a = rotatiehoek over -a) hebben we (zie figuur 4):

figuur 4 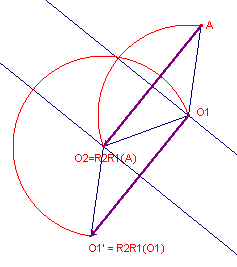rotatie4 Wegens de rotaties over tegengestelde hoeken is nu:
O1O1' // OO2.
De middelloodlijnen van deze lijnstukken zijn dus evenwijdig.
Het centrum van de som is in dit geval dus een oneigelijk punt (het oneigenlijk snijpunt van de beide middelloodlijnen).
We hebben dus een translatie over een vector waarvan de lengte gelijk is aan twee keer de afstand tussen die middelloodlijnen.

4. Sylvester's Rotator begin pagina
James Joseph Sylvester (1814-1897, Engeland) vond rond 1870 een stangenmechanisme (Eng. linkage) uit, waarmee het mogelijk is een figuur te roteren.
De "rotator" is gebaseerd op een scharnierende ruit met twee extra stangen waarvan de lengte gelijk is aan de zijde van de ruit (zie figuur 5).

figuur 5 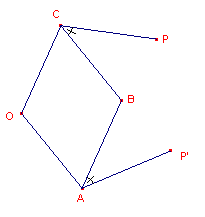rotatie5 De punten O, A, B, C zijn scharnierend.
De hoeken PCB en P'AB zijn gelijk en vast.
Het geheel draait om het vaste punt O.
Indien P figuur beschrijft, dan beschrijft P' een daarmee congruente figuur die om O geroteerd is.

Klik hier Animatie voor een CabriJavapplet van de rotator.
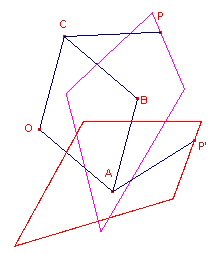figuur 6 rotatie6 In figuur 6 is een vierhoek (waarop P gelegen is) met behulp van de rotator gedraaid.

Opmerking
Het mechanisme wordt ook wel de "pantograaf van Sylvester" genoemd
[einde Opmerking]
figuur 7 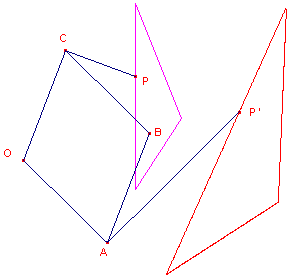rotatie7 Indien de driehoeken PCB en BAP' gelijkvormig zijn, is er sprake van een draaivermenigvuldiging tov. het punt O (zie figuur 7).
De vermenigvuldigingsfactor is dan gelijk aan BA/PC (de factor van PCB naar BAP').

Klik hier Animatie voor een CabriJavapplet voor deze afbeelding.

5. Referenties begin pagina

[1]  Cabri Java Applets - Jen-Chung Chuan, National Tsing Hua University (Taiwan) sylvester
[2] Linkages - Leo Dorst, UvA
[3] Pantographs - Museo Unimo, Italië (zie illustratie hiernaast)
[4] Meer over Sylvester - GMFW, KUN
[5] Pantograph of Sylvester - Geometry in Motion (Daniel Scher, USA)

Zie ook de pagina "Peaucellier-cel".
Zie ook de pagina "Draaivermenigvuldiging"
Zie ook de pagina "Cardioïdes met stangenmechanisme"

begin pagina
[rotaties.htm] laatste wijziging op: 05-09-05