Macro's voor figuren, ed.

Overzicht ][ Cabri-macro's

0. Overzicht
Deze pagina wordt, indien daar aanleiding voor is, aangevuld.
En mocht het wat te vaak gebeuren, dan wordt de pagina gesplitst.

			Omschrijving macro's

	1.		GelijkzDriehoekOpLijnstuk
	2.		VierkantOpLijnstuk
	3.		TrisectieLijnstuk
	4.		90º-rotaties
	5.		GuldenSnedeLijnstuk / Hoek36 / Hoek72 / GuldenRechthoek
	6.		Regelmatige 5-hoek / Regelmatige 10-hoek
	7.		Regelmatige 6-hoek / Regelmatige 8-hoek
	8.		GelijkvDriehoekOpLijnstuk
	9.		Som van twee rotaties
	10.		Punt dmv. coördinaten (in R²)
	11.		Strook om een lijnstuk
	12.		KoordeHoekBoog

1. macro:GelijkzDriehoekOpLijnstuk
Beschrijving
De macro tekent een tweetal lijnstukken die samen met een gegeven lijnstuk een gelijkzijdige driehoek vormen.

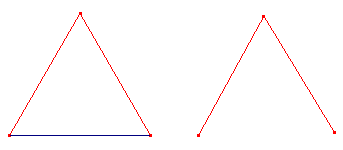De helptekst luidt:
"Constructie van een gelijkzijdige driehoek op een lijnstuk
- Selecteer 2 punten of een lijnstuk
Zijden worden geconstrueerd in tegenwijzerrichting"

Bijzonderheden
De constructie is afhankelijk van de volgorde waarin de punten worden geselecteerd cq. het gegeven lijnstuk is geconstrueerd.
Het derde punt ligt in tegenwijzerrichting tov. de beide gegeven punten.

Constructie

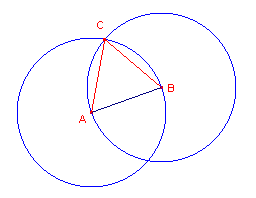Toelichting
1, 2 - punten A en B
3 - Lijnstuk(A, B)
4, 5 - Cirkel(A, AB) en Cirkel(B, BA)
6 - Snijpunt C (C ligt in tegenwijzerrichying tov. A en B)
7, 8 - Lijnstuk(A, C) en Lijnstuk(B, C)

2. macro:VierkantOpLijnstuk
Beschrijving
De macro tekent drie lijnstukken die samen met een gegeven lijnstuk een vierkant vormen.

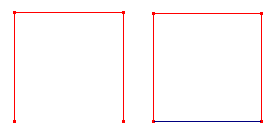De helptekst luidt:
"Constructie van een vierkant op een lijnstuk
- Selecteer twee punten of een lijnstuk
Constructie van de zijden in tegenwijzerrichting"

Bijzonderheden
De constructie is afhankelijk van de volgorde waarin de punten worden geselecteerd cq. het gegeven lijnstuk is geconstrueerd.
Het derde en vierde punt liggen in tegenwijzerrichting tov. de beide gegeven punten.

Constructie

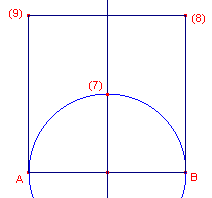Toelichting
1, 2 - punten A en B
3 - Lijnstuk(A, B)
4 - Midden(3)
5 - Loodlijn(4, 3)
6 - Cirkel(4, A)
7 - Snijpunt(5, 6)
8, 9 - PuntSpiegeling(A, 7) en Puntspiegeling(B, 7)
10, 11, 12 - Lijnstuk(B, 8), Lijnstuk(8, 9), Lijnstuk(9, A)

3. macro:TrisectieLijnstuk
Beschrijving
De macro tekent twee deelpunten die een lijnstuk in drie gelijke stukken verdelen.

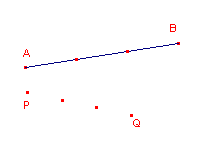De helptekst luidt:
"Verdeling van een lijnstuk in drie gelijke deellijnstukken
- Selecteer het lijnstuk (of twee punten)
Alleen de deelpunten worden geconstrueerd

Bijzonderheden
Geen

Constructie

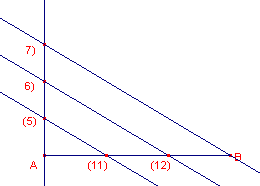Toelichting
1, 2 - punten A en B
3 - Lijnstuk(A, B)
4 - Loodlijn(A, AB)
5 - PuntOpObject(4)
6 - Puntspiegeling(A, 5)
7 - Puntspiegeling(5, 6)
8 - Lijn(7, B)
9, 10 - EvenwijdigeLijn(6, 8) en EvenwijdigeLijn(5, 8)
11, 12 - Snijpunt(9, 3) en Snijpunt(10, 3)

4. 90º-Rotaties - macro:R+90 en macro:R-90
Beschrijving
De macro's tekenen het beeld van een punt bij een rotatie over +90º (tegenwijzerrichting) en -90º (wijzerrichting).

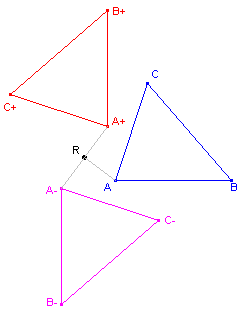De helpteksten luiden:
(R+90) "Rotatie van een punt tov. van een punt over +90 graden
- Selecteer het punt en dan het rotatiecentrum"
(R-90) "Rotatie van een punt tov. van een punt over -90 graden
- Selecteer het punt en dan het rotatiecentrum"

Bijzonderheden
Geen

Constructie

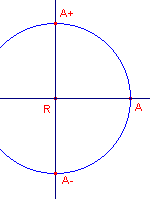Toelichting
1, 2 - A en R
3 - Cirkel(R, A)
4 - Lijn(R, A)
5 - Loodlijn(R, 4)
6, 7 - Snijpunten(5, 3)

5.1. macro:GuldenSnedeLijnstuk
Beschrijving
De macro construeert op een lijnstuk (of tussen twee punten) een punt dat het lijnstuk verdeelt in uiterste en middelste reden (fractie = (-1 +Ö5) / 2 = 0,618034...), ook wel "gulden snede" of "sectio aurea" genoemd.

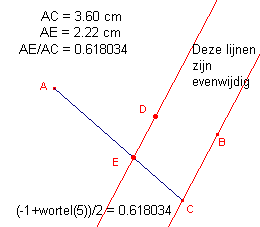In de figuur hiernaast zijn de punten D en E getekend met de macro.

De helptekst luidt:
"Verdeling van een lijnstuk in uiterste em middelste reden
- Selecteer een lijnstuk (of de eindpunten ervan)"

Bijzonderheden
Geen

Constructie

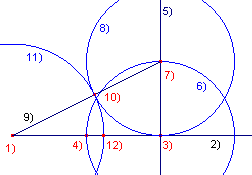Toelichting
1, 2 - Eindpunt en halve lijn
3 - PuntOpObject(2)
4 - Midden(1, 3)
5 - Loodlijn(3, 2)
6, 7 - Cirkel(3, 4) en Snijpunt(5, 6)
8 - Cirkel(7, 3)
9 - Lijnstuk(1, 7)

10, 11 - Snijpunt(9, 8) en Cirkel(1, 10)
12 - Snijpunt(2, 11)

5.2. macro:Hoek36
Beschrijving
De macro construeert een hoek van 36º op een halve lijn met als hoekpunt het beginpunt van die halve lijn .

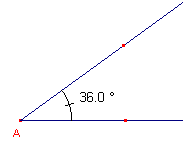De helptekst luidt:
"Constructie van een hoek van 36 graden op een halve lijn
- Selecteer het hoekpunt en de halve lijn"

Bijzonderheden
Het tweede been van de hoek staat in tegenwijzerrichting met de halve lijn.

Constructie
Bij de constructie is de macro:GuldenSnedeLijnstuk gebruikt.

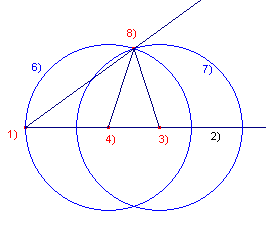Toelichting
1, 2 - Eindpunt en halve lijn
3 - PuntOpObject(2)
4 - macro:GuldenSnedeLijnstuk(1, 3)
5 - Lijnstuk(1, 4)
6 - Passer(4, 5)
7 - Passer(3, 5)
8 - Snijpunt(6, 7)
9 - HalveLijn(1, 8)

5.3. macroHoek72
Beschrijving
De macro construeert een hoek van 72º op een halve lijn met als hoekpunt het beginpunt van die halve lijn .

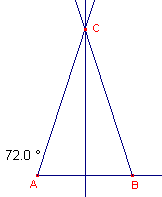De helptekst luidt:
"Constructie van een hoek van 72 graden op een halve lijn
- Selecteer het hoekpunt en de halve lijn"

Bijzonderheden
Het tweede been van de hoek staat in tegenwijzerrichting met de halve lijn.

Constructie
Bij de constructie is gebruik gemaakt van de macro:Hoek36.

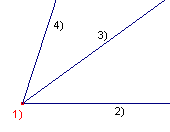Toelichting
1, 2 - Eindpunt en halve lijn
3 - macro:Hoek36(1, 2)
4 - Spiegeling(2, 3)

5.4. macro:GuldenRechthoek
Beschrijving
De macro construeert een rechthoek op een lijnstuk (de grootste zijde), waarvan de kleine zijde de middelste reden is van de grootste zijde.

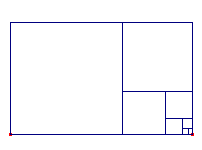De helptekst luidt:
"Constructie van een rechthoek op een lijnstuk met kleine zijde gelijk aan de middelste reden daarvan
(Gulden Snede)
- Selecteer het lijnstuk (of de eindpunten ervan)"

Bijzonderheden
De orientatie van de punten is de tegenwijzerrichting.

Constructie
Bij de constructie is gebruik gemaakt van de macro:GuldenSnedeLijnstuk.

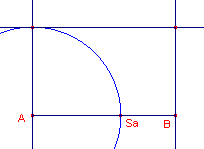Toelichting
Sa - macro:GuldenSnedeLijnstuk(A, B)
Daarna is de rechthoek met kleine zijde AS_a op de gebruikelijke wijze geconstrueerd.

6.1. macro:RegelmVijfhoek
Beschrijving
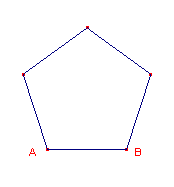
Met de macro wordt een regelmatige vijfhoek geconstrueerd op een gegeven lijnstuk (eventueel alleen bepaald door de eindpunten daarvan).

De helptekst luidt:
"Constructie van een regelmatige vijfhoek op een lijnstuk (als zijde)
- Selecteer het lijnstuk (of de eindpunten ervan)"

Bijzonderheden
De constructie is afhankelijk van de volgorde waarin de eindpunten van het lijnstuk zijn vastgelegd cq. van de volgorde van de selectie van de beide punten.
Standaard is de oriëntatie van de punten van de vijfhoek de tegenwijzerrichting.

Constructie
Bij de constructie is gebruik gemaakt van de macro:Hoek36.

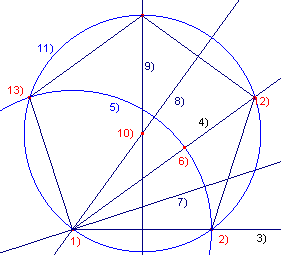Toelichting
1, 2 - Eindpunten (cq. Lijnstuk)
3 - HalveLijn(1, 2)
4 - macro:Hoek36(1, 3)
5 - Cirkel(1, 2)
6 - Snijpunt(4, 5)
7 - Bissectrice(6, 1, 2)
8 - Spiegeling(7, 4)
9 - Middelloodlijn(1, 2)
10 - Snijpunt(8, 9)
11 - Cirkel(10, 1)

12 - Snijpunt(4, 11)
13 - Snijpunt(5, 11)
14 - Veelhoek(1, 2, 12, x, 13)
(x - is niet aangegeven in de figuur)

Opmerking
Zie ook de standaard macro:Pentagram.
[einde Opmerking]

6.2. macro:RegelmTienhoek
Beschrijving
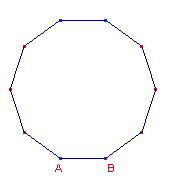
Met de macro wordt een regelmatige tienhoek geconstrueerd op een gegeven lijnstuk (eventueel alleen bepaald door de eindpunten daarvan).

De helptekst luidt:
"Constructie van een regelmatige 10-hoek op een lijnstuk (als zijde)
- Selecteer het lijnstuk (of de eindpunten ervan)"

Constructie
Bij de constructie is gebruik gemaakt van de macro:Hoek72.

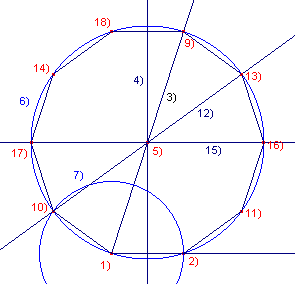Toelichting
1, 2 - Eindpunten (cq. lijnstuk)
x - HalveLijn(1, 2); x is niet vermeld
3 - macro:Hoek72(1, x)
4 - Middelloodlijn(1, 2)
5 - Snijpunt(3, 4)
en vervolgens zijn de overige hoekpunten van de tienhoek geconstrueerd via punten op de omCirkel(5, 1)

7.1. macro:RegelmZeshoek
Beschrijving
Met de macro wordt een regelmatige zeshoek geconstrueerd op een gegeven lijnstuk (eventueel alleen bepaald door de eindpunten daarvan).

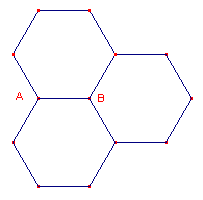De helptekst luidt:
"Constructie van een regelmatige 6-hoek op een lijnstuk (als zijde)
- Selecteer het lijnstuk (of de eindpunten ervan)"

Constructie

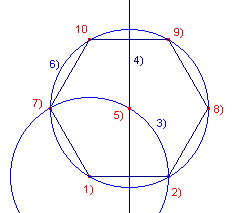Toelichting
1, 2 - Eindpunten (cq. lijnstuk)
3 - Cirkel(1, 2)
4 - Middelloodlijn(1, 2)
5 - Snijpunt(3, 4)
6 - Cirkel(5, 1)
7 - Snijpunt(6, 3)
De overige punten zijn via spiegelingen op de omcirkel geconstrueerd.

7.2. macro:RegelmAchthoek
Beschrijving
Met de macro wordt een regelmatige achthoek geconstrueerd op een gegeven lijnstuk (eventueel alleen bepaald door de eindpunten daarvan).

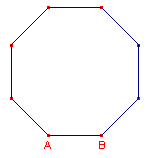De helptekst luidt:
"Constructie van een regelmatige 8-hoek op een lijnstuk (als zijde)
- Selecteer het lijnstuk (of de eindpunten ervan)"

Constructie

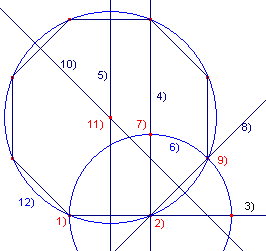Toelichting
1, 2 - Eindpunten (cq. lijnstuk)
3 - HalveLijn(1, 2)
4 - Loodlijn(2, 3)
5 - Middelloodlijn(1, 2)
6 - Cirkel(2, 1)
7 - Snijpunt(4, 6)
8 - Bissectrice(7, 2, x); x is niet vermeld
9 - Snijpunt(8, 6)
10 - Middelloodlijn(2, 9)
11 - Snijpunt(10, 5)

12 - Cirkel(11, 1)
De overige punten op de omcirkel zijn via spiegelingen verkregen.

8. macro:GelijkvDriehoekOpLijnstuk
Beschrijving
Met de macro wordt op een lijnstuk als zijde een driehoek geconstrueerd die direct gelijkvormig is met een gegeven driehoek.

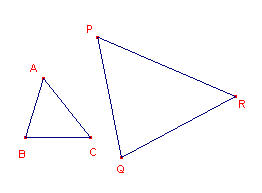De helptekst luidt:
"Driehoek PQR op een gegeven lijnstuk QR, gelijkvormig met een gegeven driehoek ABC
- Selecteer de drie hoekpunten (volgorde!) en de twee eindpunten (volgorde!)"

De orientatie van driehoek PQR is steeds gelijk aan die van driehoek ABC.

Bijzonderheden
Alleen de zijden PQ en PR van de te construeren driehoek worden getekend.
Van driehoek ABC worden alleen de hoekpunten gebruikt.

Constructie
Bij de constructie is gebruik gemaakt van de standaard macro:KopieHoek. Deze macro brengt een hoek over naar een halve lijn.

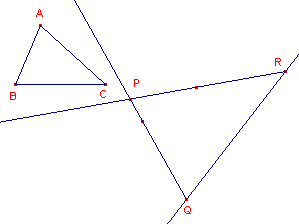Toelichting
1 - HalveLijn(Q, R)
2 - HalveLijn(R, Q)
3 - macro:KopieHoek(A, B, C, 1) = HalveLijn door Q
4 - macro:KopieHoek(A, C, B, 2) = HalveLijn door R
5 - Snijpunt(3, 4) = P
6, 7 - Lijnstuk(P, Q) en Lijnstuk(P, R)

De lijnstukken PQ en PR zijn de eindobjecten van de macro:GelijkvDriehoekOpLijnstuk.

9. Som van twee rotaties - macro:SomR2R1
Beschrijving
De macro construeert het centrum en de hoek van de som van twee rotaties met verschillende centra.

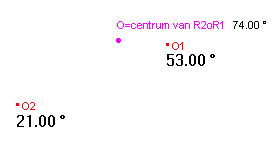De helptekst luidt:
"Centrum en hoek van de som van de rotaties (O1, h1) en (O2, h2); h1 en h2 in graden
- Selecteer O1, h1 en dan O2, h2"

Let op de volgorde van de selectie: eerst O₁ en dan O₂ (voor R₂oR₁)!

Bijzonderheden
De grootte van de rotatiehoeken moet gegeven worden in graden. Dit kan via de functie "Wijzig getallen" in het Extra-menu, gevolgd door [Ctrl]+[U] en de keuze "Graden", of met de functie "Hoek" in het Reken-menu (indien de hoeken zijn getekend).
De uitvoering wordt beëindigd door te klikken op het Cabri-werkblad. Op de gekozen positie wordt de som van de hoeken weergeven. Het centrum van de som wordt eerst dan weergegeven.
Nb.
Als de som van de hoeken gelijk is aan 360° (wat inhoudt dat we roteren over hoeken h₁ en h₂ = -h₁), dan is het centrum van de rotatie een oneigenlijk punt. Er wordt dan niets getekend. Wel wordt de som van de heoeken op het tekenblad gezet.

Constructie
In onderstaande constructie kunnen de waarden 60 en 30 vervangen worden door andere.
De macro-definitie is namelijk onafhankelijk van die waarden.

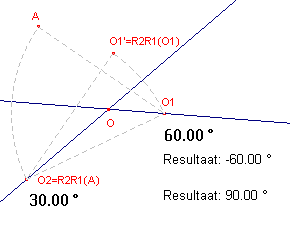Toelichting
1, 2 - punten O₁ en O₂
3, 4 - Wijzig getallen (zie Bijzonderheden), voor 60.00° en 30.00°
5 - Rekenmachine(-a), waarbij a = 60°
6 - Rotatie(O₁, O₂, 30) = R₂R₁(O₁) = O₁'
7 - Rotatie(O₂, O₁, -60) = A
8 - Middelloodlijn(O₁', O₁)
9 - Middelloodlijn(A, O₂)
10 - Snijpunt(8, 9) = O
11 - Rekenmachine(a+b), waarbij a = 60° en b = 30°

De eindobjecten van de macro zijn het punt O en het getal 90°.

Opmerking
Zie ook de pagina "Rotaties". Op die pagina staat ook een link naar een CabriJavapplet.
[einde Opmerking]

10. Punt door middel van coördinaten - macro:PuntCoord
Zie ook Opmerking

Beschrijving
De macro tekent een punt in een coördinatenstelsel dat gegeven wordt door de beide coördinaten.

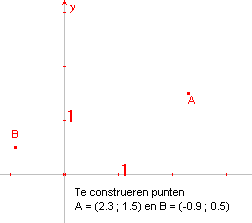De helptekst luidt:
"Constructie van een punt (x,y) in een assenstelsel
- Selecteer x en y (getallen) en een as van het assenstelsel"

Opmerking
In de figuur hiernaast zijn de coördinaten van de punten A en B eerst met de functie "Wijzig getallen" op het tekenblad gezet. Met de functie "Commentaar" zijn die getallen toegevoegd aan dat commentaar.
[einde Opmerking]

Bijzonderheden
De getallen moeten op het tekenblad zijn geplaatst met de optie "Wijzig getallen" in het Extra-menu.
Het verdient de voorkeur punten met (vaste) geheeltallige coördinaten direct te tekenen op de roosterpunten (via de Optie "Definieer rooster" uit het Layout-menu.

Constructie

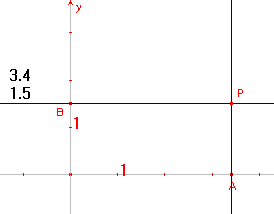Kies in het Layout-menu de functie "Toon assenstelsel".
1 - WijzigGetallen(3.5)
2 - WijzigGetallen(1.5)
3 - MaatOverbrengen(3.4 , x-as) = A
4 - MaatOverbrengen(1.5 , y-as) = B
5 - Loodlijn(A, x-as)
6 - Loodlijn(B, y-as)
7 - Snijpunt(5,6) = P

De beginobjecten van de macro zijn: "3.4", "1.5" en het assenstelsel; het eindobject is het punt P.

Opmerking
Zie de pagina "Cabri-FAQ (15)" voor een dergelijke constructie in R³.
Op de pagina "macro:PuntInR3" staat een macro beschreven die gebruik maakt van drie coördinaten.

11. Strook om een lijnstuk - macro:Strook

Beschrijving
De macro tekent een strook (rechthoek) om een lijnstuk.

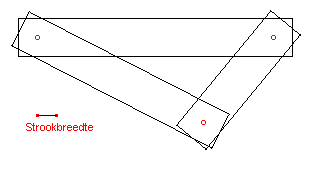De helptekst luidt:
"Constructie van een "strook"
- Selecteer een lijnstuk (of de eindpunten) en dan de halve strookbreedte (als lijnstuk)"

Bijzonderheden

[1]	Indien het basislijnstuk wordt gekozen, dan wordt het lijnstuk na uitvoering van de macro "verborgen".
[2]	Indien de eindpunten van het basislijnstuk worden gekozen, dan wordt de layout van deze punten gewijzigd. Het lijnstuk zelf blijft in dit geval zichtbaar.

Constructie

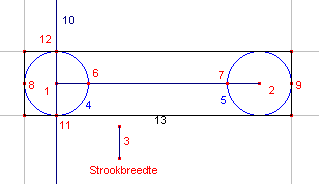1,2,3 - Lijnstuk en strookbreedte
4, 5 - Passer(1,3) en Passer(2,3)
6, 7 - Snijpunten(lijnstuk, 4) en Snijpunten(lijnstuk, 5)
8, 9 - Puntspiegeling(6, 1) en Puntspiegeling(7, 2)
10 - Loodlijn(lijnstuk, 1)
11, 12 - Snijpunten(4, 10)
niet genummerd: EvenwijdigeLijn(11, lijnstuk) en (12, lijnstuk)
niet genummerd: EvenwijdigeLijn(8, 10) en (9 ,10)
13 - Rechthoek bepaald door de snijpunten van deze lijnen

De beginobjecten van de macro zijn het lijnstuk en de (halve) strookbreedte; het eindobject is 13.

12. macro:KoordeHoekBoog
Zie ook Opmerking 2

Beschrijving
De macro tekent de verzameling van de punten P van waaruit een lijnstuk wordt gezien onder een gegeven hoek.

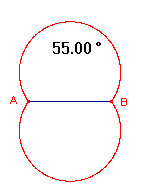De helptekst luidt:
"Constructie van de meetkundige plaats waaruit een koorde onder een gegeven hoek wordt gezien
- Selecteer de koorde en de hoek (in graden) of drie punten die de hoek bepalen"

Bijzonderheden
De macro kan (vooralsnog) niet worden gebruikt bij figuren die dienen als basis voor een CabriJavapplet.
De macro werkt (uiteraard) niet (juist) voor hoekwaarden groter dan 180º of kleiner dan 0º.

Constructie
De constructie is gebaseerd op het snijden van twee (halve) lijnen die in de eindpunten van het gegeven lijnstuk een variabele, maar natuurlijk van de gegeven hoek afhankelijke, hoek maken met dat lijnstuk.
Het snijpunt van die twee lijnen bepaalt dan de gewenste meetkundige plaats.
Uitgaande van een "kijkhoek" van 55º laten we de ene (halve) lijn roteren van -125º tot +125º.
De hoek die de andere lijn maakt met het lijnstuk passen we daaraan aan.

Klik hier voor een animatie met CabriJava van deze opzet.

Voor de rotatie van de tweede lijn worden twee Cabri-functies gebruikt: "abs" en "sign".
De functie "abs" berekent de absolute waarde van een uitdrukking.
De functie "sign" berekent het signum (teken) van een uitdrukking (-1 voor negatieve waarden, 0 voor gelijk aan 0, +1 voor positieve waarden).
De rotatie wordt bewerkstelligd door het verplaatsen van een punt P op het lijnstuk AB. P bepaalt dan een numerieke variabele (hieronder verder met p aangegeven) die waarden tussen 0 en 2 aanneemt.

De constructiestappen zijn als volgt, uitgaande van een gegeven lijnstuk AB en een hoek h.

figuur 12b		1 - PuntOpObject(AB) = P 2 - Afstand(A, P) 3 - Afstand(A, B) 4 - Rekenmachine / zie verder figuur 12b Het resultaat van de berekening is het getal p, dat waarden aanneemt tussen 0 en 2. Vervolgens tekenen we een lijn ten behoeve van de rotatie om het punt A. We nemen de lijn door de punten A en B (zie figuur 12c)
figuur 12c		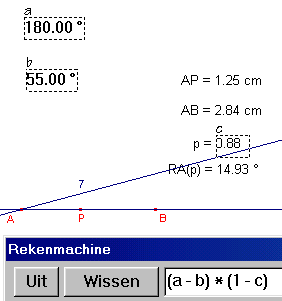5 - Lijn(A, B) Deze lijn moet worden geroteerd over hoeken van +125º tot -125º. We kunnen dat bereiken met de functie R_A(p) = (180º - h) * (1 - p) waarin h de "kijkhoek" is. Deze functie geeft de rotatiehoek van de lijn met rotatiecentrum A We berekenen de functiewaarde met de Rekenmachine. 6 - Rekenmachine / zie verder figuur 12c. 7 - Rotatie(5, A, R_A)
Nb. De constante 180º is voorafgaande aan de berekening eveneens op het Cabri-werkblad geplaatst. Voor de definitie van de macro zou in dit geval ook de waarde 180º als "Beginobject" moeten worden aangewezen. Dit is wat onhandig. Zie voor de definitie van de macro daarom Opmerking 1.
figuur 12d		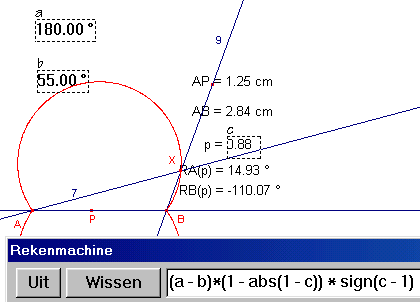De functie die de rotatiehoek geeft voor de rotatie met centrum B is R_B(p) = (180º - h) * (1 - abs(1 - p)) * sign(p - 1) 8 - Rekenmachine / zie verder figuur 12d 9 - Rotatie(5, B, R_B) 10 - Snijpunt(7, 9) = X 11 - MeetkundigePlaats(X, P)

Opmerkingen
[1]
Voor de definitie van de macro is handig in de beide functies (in de Rekenmachine) de variabele a te vervangen door "4 * invtan(1)"; dus opvolgend:
R_A(p) = (4 * invtan(1) - h) * (1 - p)
R_B(p) = (4 * invtan(1) - h) * (1 - abs(1 - p)) * sign(p - 1)
Het is dan niet noodzakelijk de waarde van 180º vooraf op het Cabri-werkblad te plaatsen.
De beginobjecten van de macro zijn dan (in eerste instantie): de hoek en het lijnstuk AB.
Het eindobject is de meetkundige plaats.
De macrodefinitie kan eventueel worden uitgebreid door het lijnstuk te kiezen en een hoek bepaald door drie punten.
[2]
Op de pagina "Cabri-FAQ (18)" wordt de "gewone" constructie van de meetkundige plaats beschreven.
Zie eventueel ook de pagina "Middelpunts- en omtrekshoeken".
[einde Opmerking]

[figuren.htm] laatste wijziging op: 18-01-18 (14-01-2001)