Middelpunts- en omtrekshoeken

Overzicht

Definities en stellingen
Constructie
Referenties

Zie ook: Omtrekshoeken (Cabri-werkblad)

1. Definities en stelllingen

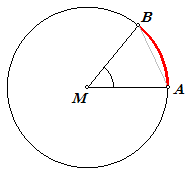Hoek AMB is een deel van de volle hoek (360º) bij punt M.
Hoek AMB is een zogenoemde middelpuntshoek van de cirkel.
De grootte van die hoek wordt bepaald door de lengte van de koorde AB van de cirkel. Ook de lengte van de boog AB wordt door die koorde bepaald.

Het is gebruikelijk de grootte (niet de lengte) van boog AB uit te drukken in zogenoemde booggraden.

Daarbij geldt de afspraak dat een booggraad de boog is die behoort bij een middelpuntshoek van 1º.
We schrijven dan: bg(AB) = 1º, als hoek AMB gelijk is aan 1°.

Opmerking. De grootte van een boog is daarmee onafhankelijk van de lengte van de straal van de cirkel.

Gevolg
Een middelpuntshoek is gelijk aan de de onderspannende boog van die hoek.

Stelling 1

Bij gelijke middelpuntshoeken van dezelfde cirkel behoren gelijke koorden en gelijke bogen.

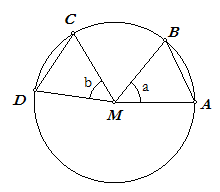Bewijs. Zijn AMB en CMD gelijke middelpuntshoeken (aangegeven met a en b). We verplaatsen nu hoek a zo, dat deze samenvalt met hoek b. Hierdoor valt been AM samen met been CM en been BM samen met been DM.
De driehoeken AMB en CMD zijn daarmee congruent (ZHZ), zodat inderdaad AB = CD.
Dat de bogen AB en CD gelijke grootte hebben volgt direct uit bovengenoemde afspraak:
bg(AB) = aº en bg(CD) = bº en omdat a = b geldt eveneens bg(AB) = bg(CD).¨

Op analoge wijze kunnen we bewijzen dat:

Stelling 2

a. Bij gelijke koorden van dezelfde cirkel behoren gelijke middelpuntshoeken en gelijke bogen.
b. Bij gelijke bogen van dezelfde cirkel behoren gelijke middelpuntshoeken en gelijke koorden.

Opmerking. Men zegt vaak in plaats van 'onderspannende boog', dat een middelpuntshoek op de betreffende boog staat.

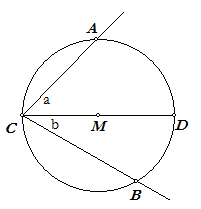
Definitie
Een omtrekshoek van een cirkel is een hoek waarvan het hoekpunt op die cirkel ligt terwijl de benen die cirkel snijden.

Opmerking. Binnen een omtrekshoek ligt een boog van de cirkel. Men zegt dat de omtrekshoek op die boog staat (het is een onderspannende boog van de omtrekshoek.

Stelling 3

Een omtrekshoek is gelijk aan de helft van de boog waarop hij staat.

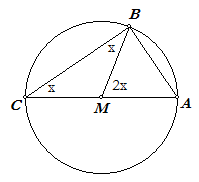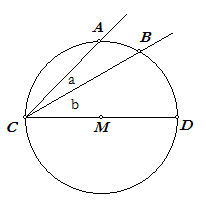
Bewijs. In nevenstaande figuur is hoek AMB (middelpuntshoek) gelijk aan 2x. Dus geldt: bg(AB) = 2x.
Driehoek MBC is gelijkbenig, dus geldt volgens de stelling van de buitenhoek, dat hoek C gelijk is aan x.
Dus: C = ½bg(AB)
We bekijken vervolgens de beide andere mogelijkheden voor de ligging van het middelpunt M van de cirkel:

1. M ligt binnen de omtrekshoek;
2. M ligt buiten de omtrekshoek.


1. Is nu ACM = a en BCM = b, dan is ACM = ½bg(AD) en BCM = ½bg(BD), zodat: ACB = a + b = ½bg(AD) + ½bg(BD) = ½( bg(AD) + bg(BD) ) = ½bg(AB)	2. Is ACM = a + b en BCM = b, dan is ACM = ½bg(AD) en BCM = ½bg(BD), zodat: ACB = a = ½bg(AD) - ½bg(BD) = ½( bg(AD) - bg(BD) ) = ½bg(AB) ¨

Stelling 4

Een hoek waarvan het hoekpunt op een cirkel ligt terwijl het ene been de cirkel snijdt en het andere de cirkel raakt, is gelijk aan de helft van de boog binnen die hoek.

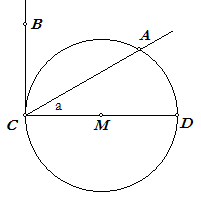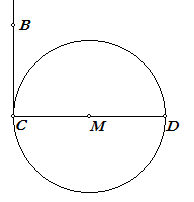
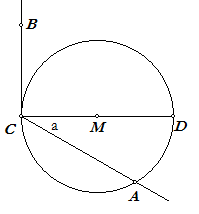
Bewijs.
Indien het middelpunt M op het snijdende been ligt, is boog CD gelijk aan 180º terwijl hoek C gelijk is aan 90º.
Dus: C = ½bg(CD).
Ligt M binnen de hoek, en is ACD = a, dan is ACB = a + 90º = ½bg(AD + 180º) = ½bg(ADC).
Ligt M buiten de hoek, en is ACD = a, dan is ACB = 90º - a = ½bg(DAC) - ½bg(AD) = ½bg(AC) ¨

Gevolg
Een raaklijn aan een cirkel en een koorde naar het raakpunt van die raaklijn kunnen worden opgevat als een omtrekshoek.

Definities
Een binnenomtrekshoek van een cirkel is een hoek waarvan het hoekpunt binnen de cirkel ligt.
Een buitenomtrekshoek is een hoek waarvan het hoekpunt buiten de cirkel ligt en waarvan de benen de cirkel snijden of raken.

Stelling 5

Een binnenomtrekshoek is gelijk aan de halve som van de bogen binnen die hoek en de bijbehorende overstaande hoek.

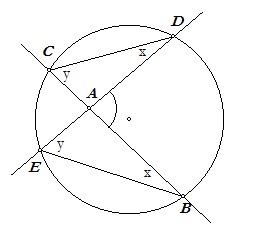Bewijs. In de figuur is:
A = x + y (buitenhoek bij driehoek ACD).
Dus:
A = ½bg(CE) + ½bg(BD) = ½( bg(CE) + bg(BD) ) ¨

Stelling 6

Een buitenomtrekshoek is gelijk aan het halve verschil van de bogen binnen die hoek.

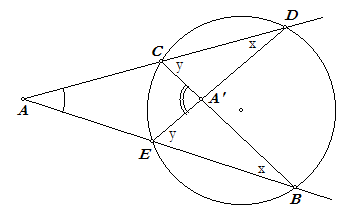Bewijs. In de figuur is:
A' = x + y (buitenhoek bij driehoek A'CD)

Dan is in vierhoek AEA'C:
A = 360º - 2 · (180º - y) - (x + y) = y - x = ½bg(BD) - ½bg(CE), zodat:
A = ½( bg(BD) - bg(CE) ) ¨

2. Constructie

Gegeven is een hoek met grootte x en een lijnstuk AB. Construeer een punt X zo, dat AXB = x.

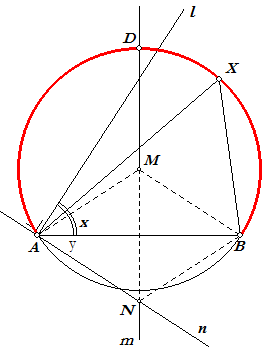Oplossing. We leggen de gegeven hoek x vast in het eindpunt A van het lijnstuk AB:
x = hoek tussen de halve lijn l en AB
De loodlijn n in A op l snijdt de middelloodlijn m van het lijnstuk AB in N.
Het punt M is het spiegelbeeld van N in AB.
De cirkel met middelpunt M door A (en B) is dan drager van (een deel van) de meetkundige plaats van de punten X met AXB = x.
Deze gedeeltelijke meetkundige plaats is bg(ADB).

Bewijs. Zij NAB = y. Dan is y = 90º - x, zodat ANB = 180º - 2 · (90º - x) = 2x
Dus ook:
AMB = 2x, zodat bg(AB) = 2x (middelpuntshoek)
Voor een punt X op bg(ADB) geldt dan:
AXB = ½bg(AB) = ½ · 2x = x ¨

Opmerkingen
1. Deze constructie wordt wel 'KoordeHoekBoog-constructie' genoemd.
2. Het spiegelbeeld van bg(ADB) in AB is het andere deel van de meetkundige plaats van de punten X met AXB = x.

3. Referenties

¤ Zie ook:
- de pagina "Cabri-FAQ (18) - Hoe teken je de verzameling punten van waaruit een lijnstuk onder een gegeven hoek wordt gezien?";
- de paragraaf KoordeHoekBoog op de pagina: "Macro's voor figuren ed." (waarop een beschrijving van een Cabri-macro voor de constructie staat);
- de pagina "Proposities III-20, III-21, waarop het verband tussen omtrekshoek en middelpuntshoek uit Euclides' Elementen is opgenomen.

[p : midomtr.htm] laatste wijziging op: 11-11-2008 (09-11-2008)