Orthogonale hyperbool en driehoek

Overzicht ][ ProjMeetkunde | Meetkunde

Overzicht terug

  1. Inleiding cabrisignal
  2. Driehoek en hoogtepunt  cabrisignal
         Stelling (probleem) van Poncelet-Brianchon
  3. Bijzondere orthogonale hyperbolen cabrisignal
         Kiepert-, Jerabek- en Feuerbach-hyperbool
  4. De asymptoten en het middelpunt cabrisignal
  5. Download

1. Inleiding terug
Op deze pagina wordt vaak gebruik gemaakt van de Stelling van Pascal (Blaise Pascal, 1623-1662, Frankrijk):

Stelling 1
Van een zeshoek (niet noodzakelijk convex) waarvan de hoekpunten op een kegelsnede liggen, zijn de snijpunten van de drie paren overstaande zijden verschillend en collineair (en omgekeerd).
. 
figuur 1 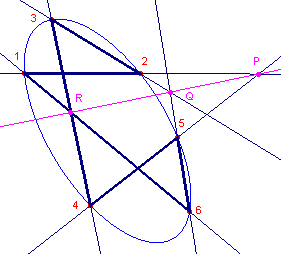orthdrie1 Geven we de hoekpunten van de zeshoek aan met 1,2,3,4,5,6 en geldt
12 /\ 45 = P, 23 /\ 56 = Q en 34 /\ 61 = R
dan liggen volgens Stelling 1 de punten P, Q en R op een rechte lijn.
Die rechte lijn wordt wel Pascal-lijn genoemd.

/\ betekent dus "doorsneden met".

Opmerking
Zie ook de pagina "De stellingen van Pascal en Brianchon voor cirkels" en de pagina "Transversalen".
[einde Opmerking]
.
Stelling 2
Snijdt een lijn een hyperbool in de punten A en B en de asymptoten daarvan in X en Y (zie figuur 2a), dan is AX = BY.

Bewijs:

figuur 2a 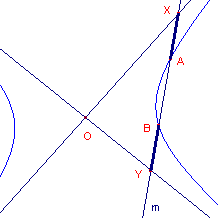orthdrie2

  

 We leveren het bewijs met behulp van de stelling van Pascal.
Een hyperbool kan worden vastgelegd door één punt en beide asymptoten. Immers de asymptoten bepalen de raaklijnen in de 'oneigenlijke' punten van de hyperbool (beide punten dubbeltellend).

Nb.
Het oneigenlijke punt X van een lijn geven we in de figuren en in de tekst aan met 'X»'.
De oneigenlijke rechte geven we in de tekst aan met l».
figuur 2b 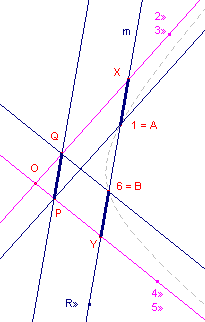orthdrie2b We leggen de hyperbool vast met de punten 1, 2», 3», 4», 5».
De punten 2» en 3» vallen samen; evenals de punten 4» en 5».
23 is de eerste asymptoot; 45 is de tweede asymptoot.
We bekijken nu de zeshoek 123456, waarbij 6 (=B) het nog  te construeren (tweede) snijpunt is van een lijn m door 1 (=A) met de hyperbool.
We voeren de constructie als volgt uit:
   12 /\ 45 = P
   23 /\ 56 = Q (nog niet bekend, maar liggend op de Pascal-lijn)
   34 /\ 61 = l» /\ m = R».
Waarmee de Pascal-lijn bekend is: de lijn door P evenwijdig aan de lijn m.
Deze snijdt 23 dus in Q.
De lijn 56 is nu de lijn door Q // 45.
Het punt 6 (=B) is dan het snijpunt van deze lijn en de lijn m.

Uit de parallellogrammen PAXQ en PYBQ volgt nu eenvoudig dat
AX = BY.¨

Opmerkingen
[1]
Door de lijn m telkens een andere positie te geven kunnen meerdere punten van de hyperbool geconstrueerd worden.
Klik hier Anmatie voor een CabriJavapplet ter illustratie.

[2]
figuur 2c 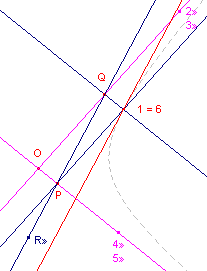orthdrie2c Op analoge wijze kan de raaklijn in een punt (1) van een hyperbool worden geconstrueerd.
We laten dan het te construeren punt 6 samenvallen met het (gegeven) punt 1.
De te construeren lijn is dan de lijn 61.
Nu hebben we (zie figuur 2c):
   12 /\ 45 = P
   23 /\ 56 = Q
   34 /\ 61 = l» /\ 61 = R»
R» ligt op de lijn PQ (de Pascal-lijn). De raaklijn (61) is dan de lijn door 1 evenwijdig met de Pascal-lijn. ¨

[einde Opmerkingen]

2. Driehoek en hoogtepunt terug
Door de hoekpunten A,B,C van een driehoek en het hoogtepunt H gaan alleen hyperbolen (zoals gemakkelijk is na te gaan).

We zullen laten zien, dat dit alleen orthogonale hyperbolen zijn.
Klik hier Anmatie voor een CabriJavapplet die dit illustreert.

Deze eigenschap staat bekend als het Probleem van Poncelet-Brianchon (Jean Victor Poncelet, 1788-1867,  en Charles Julien Brianchon, 1785-1864, beiden Frankrijk).

Zie voor een analytische behandeling de pagina's "Het probleem van Poncelet-Branchon" en "Euler-cirkels".

We kiezen nu een lijn m die de richting van één van de asymptoten bepaalt.
We construeren nu de richting n van de tweede asymptoot.

Constructiebeschrijving
De punten ABCH geven we opvolgend aan met 1234. Het punt 5» is het oneigenlijke punt van de lijn m.
We zien dat hiermee de hyperbool is vastgelegd (5 punten).
Het punt 6» is het oneigenlijke punt van de de lijn n.

figuur 3a orthdrie3 Op de in de hyperbool beschreven zeshoek 123456 passen we de stelling van Pascal toe (zie ook de constructie in Stelling 2).
12 /\ 45 = P
23 /\ 56 = Q», immers 56 = l»
De Pascal-lijn van de zeshoek is nu bekend. Het is de lijn door P evenwijdig aan BC.
R = 34 /\ 61
R ligt op de Pascal-lijn en op 34.
61 is dus de lijn door A en R.

De lijn AR bepaalt dus de richting van de tweede asymptoot.
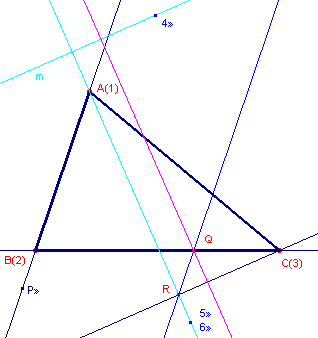figuur 3b orthdrie3b We kunnen deze tweede asymptoot zelf ook construeren. Zie daartoe figuur 3b.
We gaan uit van de zeshoek 123456, waarbij 1 = A, 2 = B, 3 = C, 4» = richting 1e asymptoot, 5» = 6» (het raakpunt op de 2e asymptoot, en liggen dus op AR).
We hebben nu:
12 /\ 45 = 12 /\ l» = P»
en
34 /\ 61 = R
De lijn PR (evenwijdig door R aan AB) is dus de Pascal-lijn.
Nu is ligt 23 /\ 56 = Q ook op de Pascal-lijn, zodat de lijn door Q evenwijdig aan AR de gewenste asymtoot zelf is. ¨

Bovenstaande constructie heeft een belangwekkend gevolg (geformuleerd in Stelling 3):

Stelling 3
Door de hoekpunten A,B,C en het hoogtepunt H gaan alleen orthogonale hyperbolen.
(Stelling van Poncelet-Brianchon)

Bewijs:
We zullen aantonen, dat de lijnen r en s (de richtingen van de asymptoten) loodrecht op elkaar staan.

figuur 4 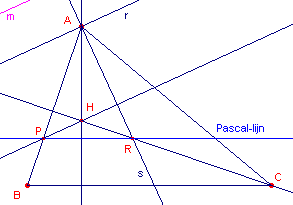orthdrie4 De lijn r is de richting van de 1e asymptoot en gaat door het punt A.
Via bovenstaande constructie hebben we verder (zie ook figuur 3a):
AH _|_ PR (immers AH _|_ BC) en CH _|_ AB.
H is dus ook hoogtepunt van driehoek APR.
PH staat dus loodrecht op AR (= s).
Maar PH // r, dus r _|_ s.
De asymptoten van hyperbolen door A, B, C, H staan dus altijd loodrecht op elkaar. ¨

De omgekeerde stelling geldt eveneens.

Stelling 4
Iedere orthogonale hyperbool die door de hoekpunten van een driehoek gaat, gaat ook door het hoogtepunt van die driehoek.

Bewijs:
Ook hier bewijzen we met de Stelling van Pascal.

figuur 5 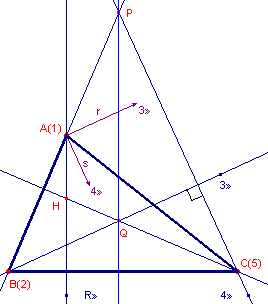orthdrie5 We gaan uit van driehoek ABC, genummerd als 125.
De punten 3» en 4» zijn oneigenlijke punten die de richtingen van de orthogonale hyperbool bepalen (zie r en s, aangegeven als vectoren, met r _|_ s).
Het punt 6 (= H; op de kegelsnede) kiezen we op de hoogtelijn uit A (van driehoek ABC).
Nu is voor zeshoek 123456:
12 /\ 45 = P en 34 /\ 61 = l» /\ AH = R».
De lijn door P evenwijdig met AH is dus de Pascal-lijn van de zeshoek.
Zij nu 23 /\ 56 = Q.
Q is dus het snijpunt van de lijn door P evenwijdig met r en de Pascal-lijn en H ligt dus op CQ.
Uit de constructie volgt, dat Q het hoogtepunt is van driehoek PBC (immers PQ // AH _|_ BC en BQ // r _|_ PC).
Dus CQ _|_ PB.
Waaruit volgt dat H (= 6) het hoogtepunt is van driehoek ABC. ¨

Gevolg
Een fraai vervolg op de constructie is Stelling 4 laten we hieronder volgen.

figuur 6 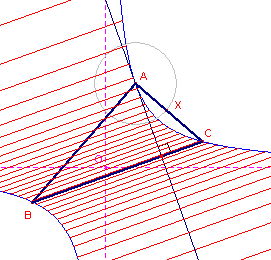orthdrie6 We gaan nu uit van een in C rechthoekige driehoek ABC.
Het punt H valt dan samen met het punt C (5 = 6). De lijn 56 gaat dan over in de raaklijn aan C aan de hyperbool.
Maar nog steeds geldt dan 56 _|_ 12.
Zodat
Bij een in een orthogonale hyperbool ingeschreven rechthoekige driehoek staat de raaklijn aan de hyperbool in de rechte hoek loodrecht op de hypothenusa
of ook
Draait een in een orthogonale hyperbool ingeschreven rechthoekige driehoek om het hoekpunt met de rechte hoek, dan beweegt de hypothenusa steeds evenwijdig.

Klik hier Anmatie voor een CabriJavapplet die dit illustreert.

3. Bijzondere orthogonale hyperbolen terug

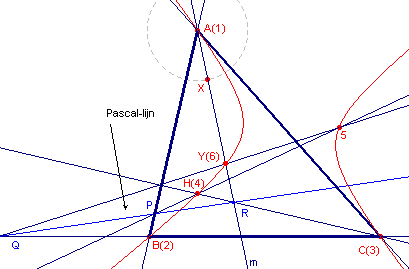figuur 7 orthdrie7 Gaan we uit van een orthogonale hyperbool die omgeschreven is om een driehoek ABC, dan gaat een dergelijke hyperbool altijd door het hoogtepunt H van ABC (Stelling 4).
Voor de constructie van die hyperbool nemen we de stelling van Pascal weer als uitgangspunt.
ABC nummeren we als 123, 4 = H en punt 5 is willekeurig.
We construeren nu op een willekeurige lijn m door A(=1) het zesde hoekpunt van de zeshoek.
De meetkundige plaats van 6(=Y) is nu de orthogonale hyperbool als de lijn m om A draait (via het punt X op een cirkel met A als middelpunt).

Gevolg
Uit de constructie van de hyperbool blijkt, dat bij elk punt 5 een bijbehorende hyperbool bestaat.
Valt 5 samen met éen van de voetpunten van de hoogtelijnen op de zijden, dan ontaardt de hyperbool in twee loodrecht op elkaar staande lijnen.
Zie ook de CabriJavapplet aan het begin van paragraaf 2.
[einde Gevolg]

Kiepert-, Jerabek- en Feuerbach-hyperbool terug

figuur 8a 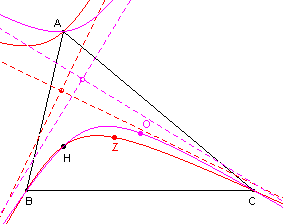orthdrie8 We kiezen als 5e punt het zwaartepunt Z van de driehoek. We krijgen dan de Kiepert-hyperbool.
Zie ook de pagina "Probleem van Lemoine en de stelling van Kiepert".

Kiezen we het punt O, het middelpunt van de omcirkel van driehoek ABC, dan krijgen we de Jerabek-hyperbool.
figuur 8b 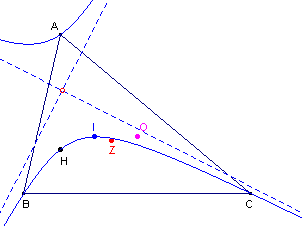orthdrie8b Kiezen we I, het middelpunt van de incirkel van driehoek ABC, dan geeft dit de Feuerbach-hyperbool.

Overigens is het niet zo, dat verschillende (5e) punten in het vlak steeds een andere hyperbool geven.
Zie hiervoor bijvoorbeeld de pagina "Probleem van Lemoine" in verband met andere punten die op de Kiepert-hyperbool liggen.

Zie verder ook paragraaf 4 voor de (meetkundige) plaats van de middelpunten van deze hyperbolen.

Klik hier Animatievoor een CabriJavapplet waarmee deze orthogonale hyperbolen kunnen worden bekeken.

4. De asymptoten en het middelpunt terug
Zoals gemakkelijk is na te gaan, kunnen we asymptoten van een orthogonale hyperbool (bepaald door de 5 punten) niet direct met de stelling van Pascal construeren.

figuur 9a 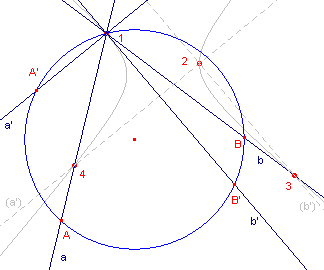orthdrie9a We gaan daarom uit van de punten 143 en 2 (opvolgend de hoekpunten van de driehoek en het 5e punt) en denken de orthogonale hyperbool bepaald door twee projectieve lijnenwaaiers met toppen 1 en 2, met lijnenparen a, (a') en b, (b').
De lijnenwaaier 2 brengen we ten behoeve van de constructie evenwijdig over naar top 1 (zie figuur 9a).
(a') wordt dan a'; (b') wordt b'.
Door het punt 1 brengen we een hulpkegelsnede (in dit geval een cirkel) aan waarop de lijnenwaaier een projectieve afbeelding insnijdt (met paren A,A' en B,B').
figuur 9b 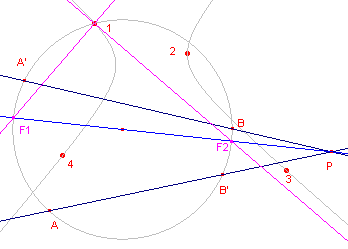orthdrie9b Uit de theorie van de projectieve afbeeldingen weten we nu, dat de snijpunten van de verbindingslijnen van overeenkomstige punten collineair zijn.
Als collineatie-as  kiezen we een lijn door het middelpunt van de hulpcirkel. Deze lijn die ook door P = AB' /\ A'B gaat, snijdt de cirkel in de dubbelpunten F1 en F2 van de projectieve afbeelding.
De lijnen 1F1 en 1F2 zijn dus de asymptoot-richtingen van de hyperbool.
Door de keuze van de collineatie-as staan deze richtingen dan loodrecht op elkaar.
figuur 9c 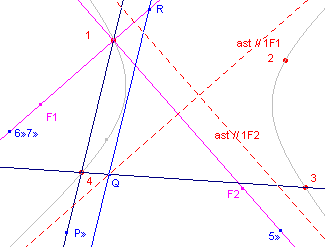orthdrie9c Op basis van de Constructiebeschrijving (gegeven in paragraaf 2, figuur  3b) kunnen we uitgaande van figuur 9b nu ook de asymptoten construeren.
We kiezen voor de asymptoot evenwijdig met 1F1 de zeshoek 1435»6»7», waarbij 5» het oneigenlijke punt is van 1F2 en 5»6» dient als raakpunt voor de gezochte asymptoot.
We hebben dan
14 /\ 56 = P»
35 /\ 71 = R

Dan is PR de Pascal-lijn, zodat we punt Q op 43 kunnen bepalen, waarbij 43 /\ 67 = Q.
De lijn door Q evenwijdig met de lijn 1F1 is dan de gevraagde asymptoot.
Op dezelfde manier vinden we de tweede asymptoot evenwijdig aan 1F2.
Het middelpunt van zo'n hyperbool is dan te vinden als snijpunt van de asymptoten.

figuur 10 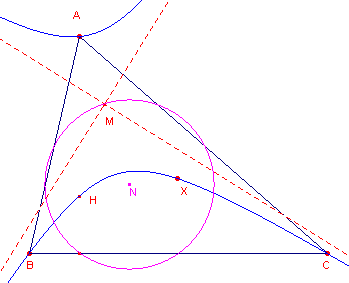orthdrie10 Klik hier Animatie voor een CabriJavapplet waarmee de meetkundige plaats van de middelpunten van de orthogonale hyperbolen kan worden bekeken.

Op basis hiervan kunnen we dus formuleren

Stelling 5
Het middelpunt van een orthogonale hyperbool die omgeschreven is om een driehoek, ligt op de negenpuntscirkel van die driehoek.

Bewijs:

figuur 11 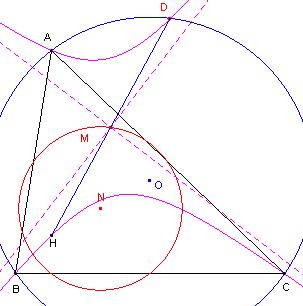orthdrie11 De omcirkel van ABC snijdt de orthogonale hyperbool nog in een punt D.
Zoals bekend (*) is de negenpuntscirkel het beeld van de omcirkel bij een vermenigvuldiging met ½ met H als centrum.
Zij M het midden van HD, dan ligt M dus op de negenpuntscirkel.
Daardoor is HD tevens middellijn van de hyperbool.
M is dus middelpunt van de hyperbool.¨

__________
(*) Zie de pagina "Over de cirkel van Feuerbach".

5. Download terug
De figuren op deze pagina, de figuren die behoren bij de CabriJavapplets en enkele gebruikte macro's kunnen in éen bestand via deze website worden gedownload.
Klik hier om het downloaden te starten (ZIP-bestand, ca. 27Kb).

bein pagina
[orthodrie.htm] laatste wijziging op: 27-12-04