De stelling van Van Aubel en algemenisering daarvan

Overzicht ][ Meetkunde

Zie ook het Cabri-werkblad "Het punt van Fermat en de driehoek van Napoleon".
Zie ook de webpagina "Bewegingen"

Overzicht terug

  1. Twee inleidende problemen; hulpstellingen  cabrisignal
         Gevolg: Stelling 3, het eerste punt van Vecten
  2. De stelling van Van Aubel  cabrisignal
        Bewijs via de hulpstellingen
  3. Rotaties
  4. Gelijkzijdige en gelijkvormige driehoeken ipv. vierkanten  cabrisignal
  5. Gelijkvormige rechthoeken en gelijkvormige ruiten  cabrisignal
  6. Rechthoeken op een koordenvierhoek  cabrisignal
  7. Referenties

1. Twee inleidende problemen; hulpstellingen terug
Probleem 1
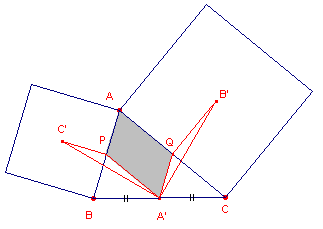
We beschrijven vierkanten op de zijden AB en AC van een willekeurige driehoek ABC (zie figuur 1).
De middelpunten C' en B' van die vierkanten verbinden we met het midden A' van de zijde BC.

figuur 1 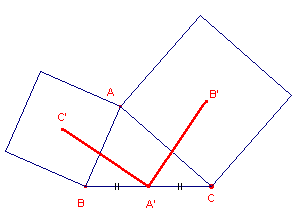vanaubel1 Klik hier cabrismall voor een CabriJavapplet van figuur 1.

We kunnen nu oa. aantonen, dat A'B' _|_ A'C' (zie Hulpstelling 1).
.
Hulpstelling 1
In figuur 1 geldt: A'B' _|_ A'C' en A'B' = A'C'
of
driehoek A'B'C' is rechthoekig en gelijkbenig.

Bewijs: zie figuur 2.

figuur 2

vanaubel2
C'A'P = A1' ; B'A'Q = A2' ; PA'Q = A = A3'

Zijn P en Q de middens van AB en AC, dan is AP//A'Q en AQ//A'P (middenparallellen).
Vierhoek APA'Q is dus een parallellogram.
Hieruit:
   C'P = AP = A'Q en B'Q = AQ = A'P
In de driehoeken A'C'P en B'A'Q is verder
   ÐP = ÐQ = 90° + ÐA (van driehoek ABC).
Beide driehoeken zijn congruent, dus A'C' = A'B'.
Verder in driehoek A'C'P:
   180° = A1' + C' + P = A1' + C' + 90° + A

Maar dan ook (daar C' in A'C'P gelijk is aan A2' in A'B'Q):
   90° = A1' + A2'+ A3'
¨

Probleem 2
In figuur 2 hebben we (volgens hulpstelling 1): driehoek A'B'C' is een gelijkbenige rechthoekige driehoek.
Deze driehoek beschouwen we afzonderlijk, maar we plakken er nog eenzelfde (gelijkvormige) in het punt A aan vast.
We bekijken dus de twee gelijkbenige rechthoekige driehoeken ABC en ADE (zie figuur 3).
Het zijn dus twee verschillende geodriehoeken die het rechtehoekpunt gemeenschappelijk hebben.

figuur 3 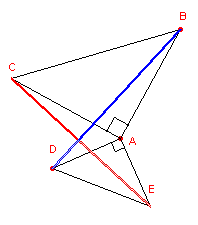vanaubel3 Klik hier cabrismall voor een CabriJavapplet van figuur 1.

De applet illustreert Hulpstelling 2.
.
Hulpstelling 2
Voor elk tweetal gelijkbenige in A rechthoekige driehoeken ABC en ADE geldt
BD = CE en BD _|_ CE.

Bewijs: zie figuur 4.

figuur 4 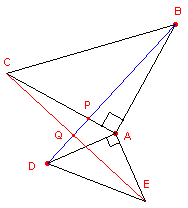vanaubel4 Driehoeken ACE en ADB zijn congruent (ZHZ).
Dus CE = BD.
Ook volgt hieruit:
   ÐECA = ÐPBA
In driehoek APB is ÐPBA + ÐAPB = 90°, zodat in driehoek PCQ geldt (gelijk op bovenstaande gelijkheid van hoeken):
   ÐECA + ÐCPQ = 90°
Dus in die driehoek is ÐQ = 90°.
De lijnstukken BD en CE staan dus loodrecht op elkaar. ¨

Gevolg terug
We moeten beide bovenstaande figuren (figuur 1 en figuur 3) natuurlijk niet los zien. We kijken naar figuur 5, waarin op de drie zijden van een willekeurige driehoek een vierkant is geplaatst.

figuur 5 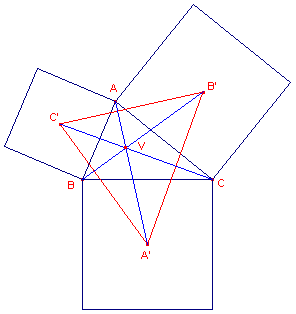vanaubel5
Stelling 3
De verbindingslijnen van de hoekpunten en de middelpunten van de overstaande vierkanten van een driehoek gaan door één punt.

Opmerking
Het gemeenschappelijke punt V heet het eerste punt van Vecten.
Zie hiervoor ook de pagina's "De figuur van Vecten" en "Probleem van Lemoine".
In stelling 4 op die pagina wordt een ander bewijs van bovenstaande stelling (stelling 3) gegeven.

Vierkanten beschreven op de zijden van een driehoek worden ook behandeld op de pagina "Constructie en stelling van Grebe".
[einde Opmerking]

Klik hier cabrismall voor een CabriJavapplet van figuur 5.

Bewijs: zie figuur 6.

figuur 6 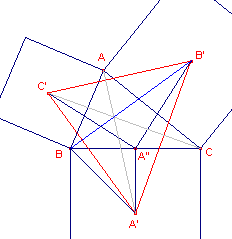vanaubel6 De driehoeken A"B'C' en A"BA' in nevenstaande figuur zijn gelijkbenige rechthoekige driehoeken die hoekpunt A" gemeenschappelijk hebben (zie hiervoor Hulpstelling 1).
De lijnen B'B en A'C' staan volgens Hulpstelling 2 loodrecht op elkaar.
De lijn B'B is dus hoogtelijn van driehoek A'B'C'.
Op dezelfde manier bewijzen we dat voor A'A en C'C.
De lijnen A'A, B'B en C'C gaan dus door één punt. ¨

2. De stelling van Van Aubel terug
We plaatsen nu op de zijden van een willekeurige vierhoek (uitwendig) een vierkant en verbinden de middelpunten van de vierkanten op de overstaande zijden.

figuur 7a 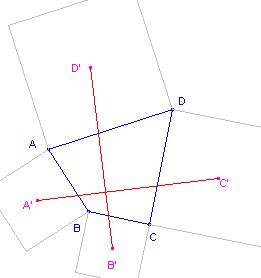vanaubel7
Stelling 4 - Stelling van Van Aubel
De verbindingslijnstukken van de middelpunten van tegenoverliggende vierkanten die (buitenwaarts) beschreven zijn op de zijden van een vierhoek, staan loodrecht op elkaar en zijn evenlang;
maw.
A'C' _|_ B'D' en A'C' = B'D'.

Klik hier cabrismall voor een CabriJavapplet van figuur 7a.

Bewijs: zie figuur 7b.

figuur 7b 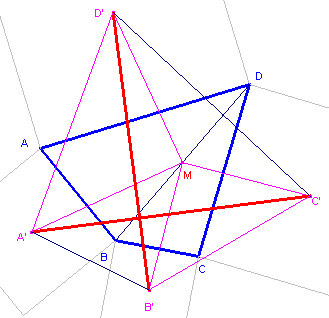vanaubel7b Zij M het midden van de diagonaal BD.
De driehoeken MA'D' en MB'C' zijn nu gelijkbenig en in M rechthoekig.
Volgens Hulpstelling 2 staan dan de lijnstukken A'C' en B'D' loodrecht op elkaar en zijn evenlang. ¨

Opmerking
Vierhoek A'B'C'D' noemen we wel de vierhoek van Van Aubel.
[einde Opmerking]

Opmerking

vanaubel De stelling is genoemd naar Henricus Hubertus van Aubel (geboren op 20 november 1830 te Maastricht; overleden op 3 februari 1906 te Antwerpen), oa. leraar wiskunde aan het Koninklijk Atheneum van Antwerpen.

In de wiskundige literatuur komt vaak de onjuiste schrijfwijze Von Aubel voor.

Met dank aan Hessel Pot (Woerden) voor het verstrekken van de biografische gegevens en de hiernaast staande foto van Henri van Aubel.

[einde Opmerking]

3. Rotaties terug
Op de pagina "Rotaties" wordt de som van twee rotaties met verschillende centra bekeken.
De resultaten daarvan kunnen we als volgt samenvatten:

Stelling 5
De som van twee rotaties met verschillende centra O1 en O2 over de hoeken a en b is
- een rotatie met centrum O over de hoek a + b, als a + b ¹ 360° (*);
- als a + b = 360°: een translatie, mits de som geen dekpunten heeft, en
- als a + b = 360°: de identieke afbeelding als de som ten minste één dekpunt heeft (en dan is elk punt een dekpunt).
of ook
de som van twee rotaties is een translatie als de rotatiehoeken gelijk zijn maar tegengesteld en is een rotatie in andere gevallen.
(*) In dit geval is ÐO1OO2 = 180° - ½(a + b).

We kunnen met behulp van stelling 5 de stelling van Van Aubel (stelling 4) eveneens bewijzen.

Bewijs van stelling 4 met rotaties.

figuur 8 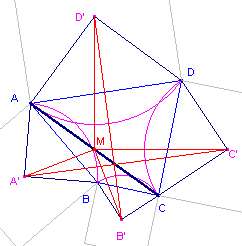vanaubel8 We beschouwen de som S van de rotaties om opvolgend D', C', B' en A' over een hoek van 90°. De afbeelding S beeldt A op A af. S is dus de identieke afbeelding (volgens stelling 5).
De som T van de rotaties om D' en C' is een rotatie over een hoek van 180°; evenals de som U van de rotaties om B' en A'.
Maar de afbeelding UT is de identieke afbeelding, waaruit volgt dat de centra van T en U moeten samenvallen met het midden M van AC, immers T(A) = C en U(A) = C.
Dit houdt in dat driehoek MD'B' het beeld van is MC'A' bij een rotatie over 90°.
De overeenkomstige lijnstukken D'B' en C'A' staan dus loodrecht op elkaar en zijn aan elkaar gelijk.. ¨

Gevolg
Algemeen bekend is dat de verbindingslijnstukken van de middens van opvolgende zijden van een vierhoek een parallelogram vormen, immers de middenparallellen zijn evenwijdig aan de de diagonalen (zie figuur 9a; zie ook de pagina "Stelling van Varignon").
We hebben nu eenvoudig:

figuur 9a figuur 9b
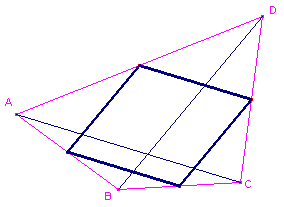vanaubel9a

Stelling van Varignon

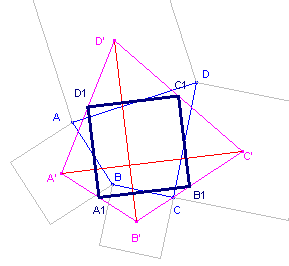 vanaubel9b
Stelling 6
De verbindingslijnstukken van de middens van de zijden van de vierhoek van Van Aubel vormen een vierkant.

Bewijs:
In figuur 9b is A'B'C'D' de vierhoek van Van Aubel, waarvan de diagonalen loodrecht op elkaar staan én gelijk zijn.
Vierhoek A1B1C1D1 (middens van de zijden) is dus een vierkant. ¨

Gaan we uit van een parallellogram ABCD, dan hebben we

Stelling 7
De vierhoek van Van Aubel van een parallellogram is een vierkant.

Bewijs: zie figuur 10.

figuur 10 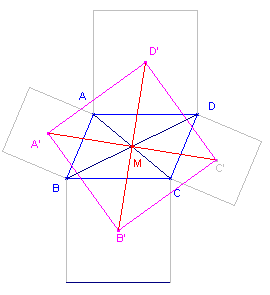vanaubel10 Het snijpunt M van de diagonalen van ABCD is punt van symmetrie van het parallellogram. Het valt dus samen met het centrum van de rotaties die eerder beschouwd zijn.
M is dus ook centrum van de puntsymmetrie van de vierhoek van Van Aubel van ABCD: A'B'C'D'.
Dit is dus eveneens een parallellogram (immers een parallellogram is de enige vierhoek met puntsymmetrie).
De diagonalen van A'B'C'D' zijn gelijk en staan loodrecht op elkaar (stelling 4).
A'B'C'D' is dus een vierkant. ¨
figuur 11 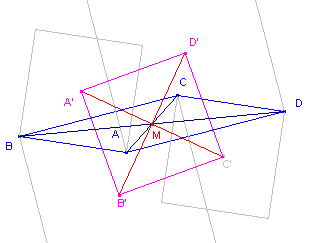vanaubel11 Opmerking
Ook indien de vierkanten binnenwaarts op de zijden van de vierhoek worden geconstrueerd, is de stelling van Van Aubel juist.
In figuur 11 is dit weergegeven voor een parallellogram als uitgangsfiguur ABCD.
[einde Opmerking]
[einde Gevolg]

4. Gelijkzijdige en gelijkvormige driehoeken ipv. vierkanten terug
We plaatsen nu om en om buiten- en binnenwaarts gelijkzijdige driehoeken op de zijden van een willekeurige vierhoek (zie figuur 12).

figuur 12 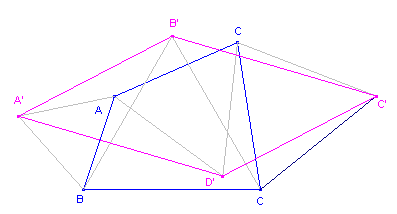vanaubel12 Klik hier cabrismall voor een CabriJavapplet van figuur 12.

We zullen bewijzen dat A'B'C'D' een parallellogram is.
.
Stelling 8a
Worden op de zijden van een vierhoek afwisselend buiten- en binnenwaarts gelijkzijdige driehoeken geconstrueerd, dan vormen de verbindingslijnstukken van de toppen van die driehoeken een parallellogram.

Bewijs: zie figuur 13a.
Ook hier kunnen we met rotaties tot een bewijs komen.

figuur 13a 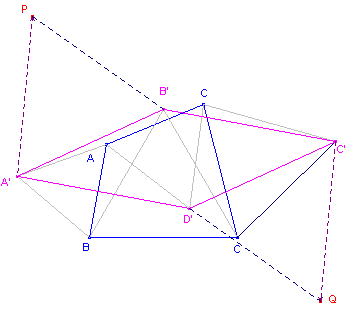vanaubel13 We kiezen rotaties met centra A', B', C' D' over 60°, waarbij die om A' en C' tegengesteld zijn aan die om B' en D'.
Gevolg: de som van deze vier rotaties beeldt A op zichzelf af.
De som van de rotaties om A' en B' is volgens stelling 5 (tweede deel) een translatie.
De translatievector is A'P (in die richting).
De som van de rotaties om C' en D' is volgens stelling 5 eveneens een translatie.
De translatievector is C'Q (in die richting).
Om dat de som van deze beide translaties de identieke afbeelding is, moeten beide lijnstukken (tegengesteld) gelijk zijn en evenwijdig.
De driehoeken A'PB' en C'QD' zijn gelijkzijdige driehoeken, waarbij nu A'P en C'Q evenwijdig en (tegengesteld) gelijk zijn

De zijden A'B' en C'D' zijn dan dus eveneens evenwijdig en tegengesteld (gelijk).
Waaruit volgt, dat A'B'C'D' een parallellogram is. ¨

Stelling 8a is een bijzonder geval van stelling 8b:

Stelling 8b
Worden op de zijden van een vierhoek afwisselend buiten- en binnenwaarts gelijkvormige driehoeken geconstrueerd, dan vormen de verbindingslijnstukken van de toppen van die driehoeken een parallellogram.
.
figuur 13b 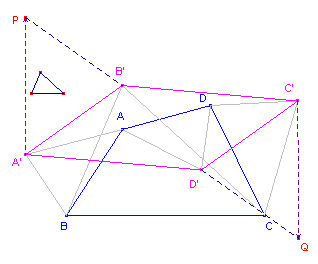vanaubel13b Bewijs: (zie figuur 13b).

Het bewijs verloopt min of meer analoog aan het bewijs van stelling 8a.
¨

5. Gelijkvormige rechthoeken en gelijkvormige ruiten terug
5.1 Gelijkvormige rechthoeken terug

figuur 14a 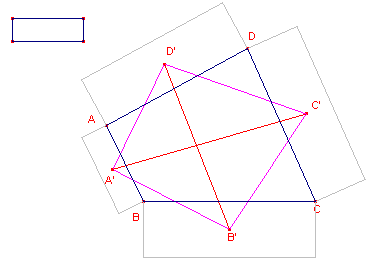vanaubel14 Wanneer we gelijkvormige rechthoeken op de zijden van de vierhoek plaatsen, waarvan de zijden telkens evenredig zijn met dezelfde zijde van een voorbeeldrechthoek (zie figuur 14a), dan gebeurt er niets spectaculairs.

Klik hier cabrismall voor een CabriJavapplet van figuur 14a.
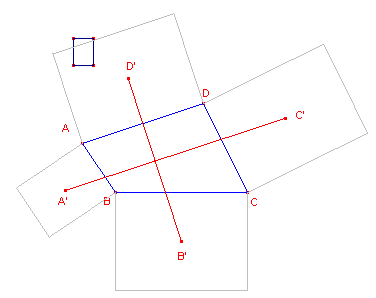figuur 14b vanaubel14b Plaatsen we echter gelijkvormige rechthoeken, waarvan de zijden om en om evenredig zijn met die van een voorbeeldrechthoek (zie figuur 14b), dan hebben we (weer):
Stelling 9
De verbindingslijnstukken van tegenoverliggende  middelpunten van buitenbeschreven gelijkvormige rechthoeken staan loodrecht op elkaar.

Klik hier cabrismall voor een CabriJavapplet van figuur 14b.

Bewijs van Stelling 9 met rotaties.

figuur 14c 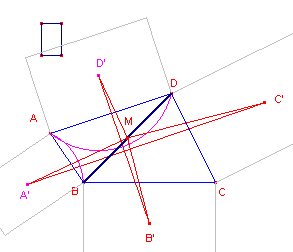vanaubel14c Het bewijs verloopt min of meer analoog aan het bewijs van Stelling 4 (met rotaties).
De som van de rotaties om opvolgend A', B', C', D' is de identieke afbeelding.
De som van de rotaties om opvolgend A' en D' is een puntspiegeling met het midden M van BD als centrum. Hierbij zijn de rotatiehoeken immers samen 180°.
Hetzelfde geldt voor de som van de rotaties om B' en C' (in tegenwijzerrichting). Nu worden echter de driehoeken MA'C' en MD'B' niet op elkaar afgebeeld.
Er is hier sprake van een draaivermenigvuldiging om M over 90º (*). De factor van de vermenigvuldiging is gelijk aan de verhouding van de lengtes van de  rechthoekszijden van de voorbeeldrechthoek.

Maar hieruit volgt echter wel, dat de lijnstukken A'C' en B'D' loodrecht op elkaar staan.
(*)
Zie voor Draaivermenigvuldiging ook de pagina's "Bewegingen" en "Draaivermenigvuldiging".
We tonen nu aan dat er hier sprake is van een draaivermenigvuldiging. Zie daartoe figuur 14d.

figuur 14d 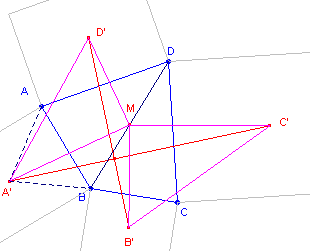vanaubel14d Zij a de grootte van ÐAA'B, dan is ook ÐCC'D daaraan gelijk. De hoeken BB'C en DD'A zijn dan gelijk aan 180° - a.
De som van de rotaties om opvolgend A', B', C' en D' is dan de identieke afbeelding (immers B wordt op B afgebeeld).
De som van de rotaties om A' en D' is een puntspiegeling (hoeken samen 180°) om het midden M van BD (immers B wordt afgebeeld op D).
ÐA'MD' (de hoek tussen de centra) is nu gelijk aan 180° -(180° -a +a) = 90° (zie stelling 5).
Zij nu M' (niet getekend) het beeld van M bij de rotatie om A' (over a), dan beeldt de rotatie om D' het punt M' weer af op M, immers M is invariant onder de som van die twee afbeeldingen.
We hebben dan A'MD' @ A'M'D' (ZZZ) waaruit volgt dat ÐMA'A = ½a en dus ÐMDA' = 90° -½a.

Dit geldt ook voor de hoeken in driehoek MC'B', waardoor MA'D' ~ MC'B' (hh). Hieruit volgt dat
   MD' : MA' = MB' : MC' = k
waarbij k dus constant is.
De draaivermenigvuldiging (M, 90°, k) beeldt dus A' op D' en C' op B' af. De hoek tussen A'C' en B'D' is dus gelijk aan de rotatiehoek, en is dus 90°, immers B'D' is het beeld van A'C'. ¨

Opmerking
Stelling 4 is een bijzonder geval van Stelling 9: kies de zijden van de rechthoek aan elkaar gelijk.
Daaruit volgt dan, in dit geval, ook dat A'C' = B'D' (de vermenigvuldigingsfactor is nu gelijk aan 1).
[einde Opmerking]

5.2. Gelijkvormige ruiten terug

figuur 15a 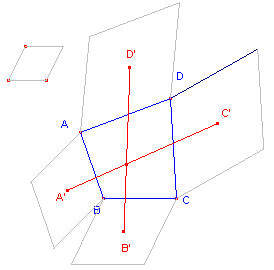vanaubel15 Als we gelijkvormige ruiten (in een zekere configuratie; zie figuur 15) op de zijden van een vierhoek plaatsen, dan zijn de bedoelde lijnstukken gelijk aan elkaar.

Klik hier cabrismall voor een CabriJavapplet van figuur 15a.

We hebben nu dus:

Stelling 10
De verbindingslijnstukken van tegenoverliggende  middelpunten van "om en om" buitenbeschreven gelijkvormige ruiten staan hebben gelijke lengte.

Bewijs: zie figuur 15b.

figuur 15b 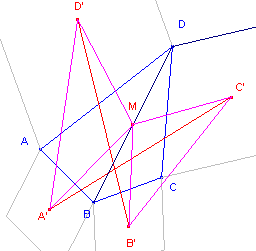vanaubel15b De verhoudingen A'B : A'A = D'D : D'A = C'D : C'C = B'B : B'C = k (constant) volgt dat we  4 draaivermenigvuldigingen kunnen beschouwen: (A', 90°, k), (B', 90°, k), (C', 90°, 1/k) en (D', 90°, 1/k).
De som van de draaivermenigvuldigingen (B'oC'oD'oA') beelden het punt B  af op B. Deze som is dus de identieke afbeelding.
De afbeelding (D'A') beeldt B af op D en is een puntspiegeling in het midden M van BD.
M is de top van de gelijkbenige driehoek MA'D', waarvan de basishoeken elk gelijk aan arctan(1/k).
Zie hiervoor Stelling 2 op de pagina "Draaivermenigvuldiging".
De tophoek is gelijk aan 180° - 2arctan(1/k).
Analoog is de afbeelding (C'oB') een puntspiegeling in het punt M. De tophoek van de gelijkbenige driehoek MB'C' is ook nu gelijk aan 180° - 2arctan(1/k).
Er is een rotatie met centrum M die A' afbeeldt op D' en C' op B', over de hoek 180° - 2arctan(1/k).

Het lijnstuk A'C' wordt du afgebeeld op het lijnstuk D'B'.
Deze lijnstukken hebben dus dezelfde lengte.  ¨

6. Rechthoeken op een koordenvierhoek terug
We plaatsen nu bijzondere rechthoeken op de zijden van een koordenvierhoek.

Stelling 11
De middelpunten van de rechthoeken (op de zijden van een koordenvierhoek), waarvan de tweede zijde gelijk is aan de overstaande zijde van de koordenvierhoek, vormen een rechthoek.
.
figuur 16 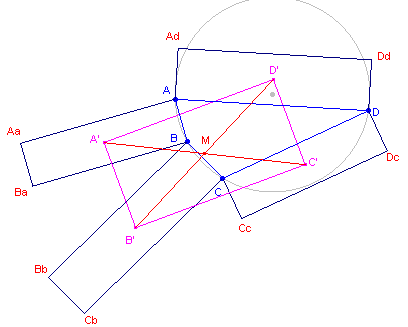vanaubel16 In de hiernaast staande figuur geldt dus voor rechthoek AAaBaB, dat
AAa = CD, BBb = AD, CCc = AB en DDd = BC.

Klik hier cabrismall voor een CabriJavapplet bij figuur 16.

Klik hier voor het bewijs van Stelling 11.

7. Referenties terug

[1] H. SCHUMANN, D. GREEN: Discovering Geometry with a Computer, Chartwell-Bratt Ltd, Bolton (UK)
[2]      M.D. DE VILLIERS: Some adventures in elementary geometry, University of Durban, Durban (ZA), 1996
[3] M.D. DE VILLIERS: "The role of proof in investigative computer-based geometry" in: J. KING (ed.), Geometry turned on, MAA Notes 41, MAA (USA), 1997
Zie ook de website van Michael de Villiers (met oa. het artikel Dual Generalizations of Van Aubel's Theorem, PDF, ca. 34kB)
[4] I.M. YAGLOM: Geometric Transformations I and II, Random House, NewYork, 1962

 

begin pagina

[vanaubel.htm] laatste wijziging op: 18-01-18