Bewijs van Stelling 11 - een bijzondere eigenschap van een koordenvierhoek

Overzicht  ][  Stelling van Van Aubel | Meetkunde

Overzicht terug

  1. Stelling 11 cabrisignal 
         Bewijs van Stelling 11
  2. Gevolg voor een gelijkbenig trapezium  cabrisignal
  3. Bijzondere configuraties
  4. Referenties
  5. Download

1. Stelling 11 terug
Onderstaande stelling, als stelling 11 vermeld op de webpagina "De stelling van Van Aubel", geeft een bijzondere eigenschap van een koordenvierhoek.
Deze hangt samen met de Stelling van Van Aubel voor een willekeurige vierhoek.

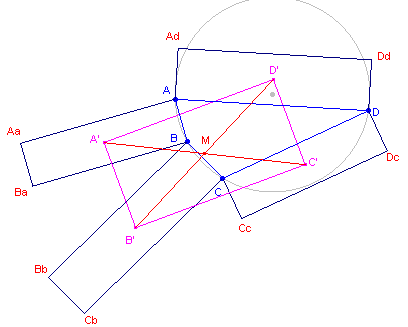vanaubel16
Stelling 1 (stelling 11)
De middelpunten van de rechthoeken op de zijden (van een koordenvierhoek), waarvan de tweede zijde gelijk is aan de overstaande zijde van die koordenvierhoek, vormen een rechthoek.

Klik hier Animatie voor een CabriJavapplet bij Stelling 1 (deze applet staat ook op de pagina "De Stelling van Van Aubel").

We gaan in eerste instantie op dezelfde manier te werk als bij de Hulpstellingen op de pagina "De Stelling van Van Aubel".
We zullen echter zien, dat dit niet tot het gewenste resultaat leidt.
De stelling, stelling 2, is er echter niet minder fraai om.

figuur 1 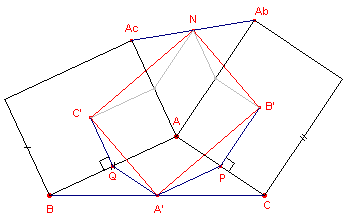vanaubel21
Stelling 2
In figuur 1 geldt A'B' _|_ A'C', waarbij B' en C' middelpunten zijn van rechthoeken op de zijden van driehoek ABC, waarvan de tweede rechthoekszijde gelijk is aan de "andere opstaande" zijde van de driehoek, en A' is het midden van AB.

Bewijs:
De punten P en Q zijn de middens van de zijden AB en AC.
AQA'P is dan een parallellogram (middenparallellen).
De driehoeken A'PB' en A'QC' zijn nu gelijkbenig (met tophoek resp. P en Q).

In deze driehoeken is nu:
ÐP = ÐQ = 90° + 180° - a = 270° - a (waarbij a de grootte van hoek A is in driehoek ABC).
Elk der basishoeken van deze driehoeken is dan gelijk aan
   ½(180° - (270° - a)) = ½a - 45°
Voor ÐA' in param AQA'P hebben we dan:
   a = x + 2(½a - 45°), waarbij x de grootte is van ÐB'A'C'
Dus x = 90°. ¨

Gevolg
Op dezelfde manier bewijzen we, dat ÐB'NC' (gebruikmakend van driehoek AAbAc) een rechte hoek is.
Via congruentieoverwegingen volgt dan, dat A'B'NC' een rechthoek is.
Waaruit dus volgt dat B'C' = A'N (beide lijnstukken zijn in figuur 1 niet getekend)
[einde Gevolg]

Opmerking
Zie ook figuur 5b op deze pagina.
[einde Opmerking]

Ook nu kiezen we een tweede driehoek XBC, die dus BC als zijde heeft.
Deze driehoek kiezen we echter zo, dat hoek X het supplement is van hoek A (ABXC is dan een koordenvierhoek).

figuur 2 vanaubel22 In dit geval vinden we (uiteraard?) geen bijzondere eigenschappen in de figuur.
Vergelijk hiermee figuur 14a op de pagina "Stelling van Van Aubel".

Kiezen we echter de tweede zijde van zo'n rechthoek gelijk aan de overstaande zijde van die zijde in de vierhoek, (zoals vermeld in Stelling 1), dan vinden we de eigenschap genoemd in stelling 1 (Stelling 11).

Bewijs van Stelling 1 (Stelling 11) terug

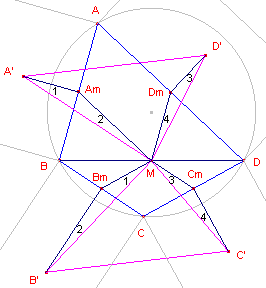figuur 3 vanaubel23 We bewijzen eerst dat A'B'C'D' een parallellogram is.
Am, Bm, Cm, Dm zijn de middens van de zijden van de koordenvierhoek.
Nu is dus:
A'Am = ½CD (constructie)
MBm = ½CD (middenparallel in driehoek CBD)
B'Bm = ½AD (constructie)
MAm = ½AD (middenparallel in driehoek ABD)
Verder is in driehoek MAmA':
ÐAm = 90° + a (waarbij a de grootte is van hoek A in de kvh).
In driehoek MBmB' is hebben we
ÐBm = 90° + 180° - c = 270° - (180° - a) = 90° + a
De driehoeken MAmA' en MBmB' zijn dus congruent.
Waaruit volgt: MA' = MB' ......(1).

Op dezelfde manier bewijzen we, dat MC' = MD' ......(2).
In figuur 3 zijn de hoeken met identieke nummering aan elkaar gelijk (vanwege de congruentie van de driehoeken waartoe ze behoren).
We gebruiken die nummering om de grootte van de hoek aan te geven; bijv. h(2) is de grootte van de hoek aangegeven met een 2.
ÐA'MD' = a + h(2) + h(4).
Nu is

a + h(2) + h(4)  =  a + (90° - a - h(1)) + (90° - a - h(3))
=  180° - a - h(1) - h(3)
=  c - h(1) - h(3)

ÐB'MC' = c - h(1) - h(3).
Dus ÐA'MD' = ÐB'MC' ......(3).
Uit (1), (2), (3) volgt dat driehoeken A'MD' en C'MB' congruent zijn.
Dus A'D' = C'B'.
Op dezelfde manier kunnen we bewijzen dat A'B' = D'C'.
A'B'C'D' is dus een parallellogram.
Eenvoudig blijkt verder, dat ÐA'MC' = ÐB'MD', zodat ook de driehoeken A'MC' en B'MD' congruent zijn.
Dus A'C' = B'D'.
A'B'C'D' heeft dus gelijke diagonalen.
A'B'C'D' is dus een rechthoek. ¨

2. Gevolg voor een gelijkbenig trapezium terug

Stelling 3
De middelpunten van de rechthoeken beschreven op de zijden van een gelijkbenig trapezium, waarvan de tweede zijde gelijk is aan de overstaande zijde, vormen een vierkant.

Klik hier Animatie voor een CabriJavapplet bij Stelling 3.

Bewijs: (zie figuur 4)

figuur 4 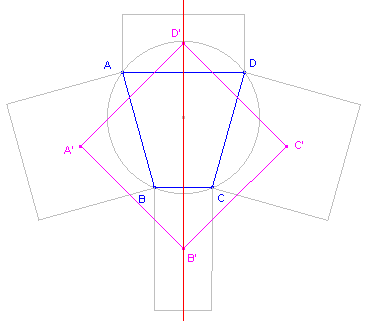vanaubel24 Een gelijkbenig trapezium is een koordenvierhoek.
De rechthoeken op beschreven op de opstaande zijden van het trapezium zijn nu vierkanten.
Daardoor is de gehele figuur lijnsymmetrisch tov. de lijn B'D'.
De rechthoek (volgens stelling 1) heeft dan twee gelijke opvolgende zijden en is dus een vierkant. ¨

[einde Gevolg]

3. Bijzondere configuraties terug
In de volgende figuren staan enkele configuraties die gebaseerd zijn op de constructie bij het gelijkbenig trapezium.

figuur 5a       figuur 5b
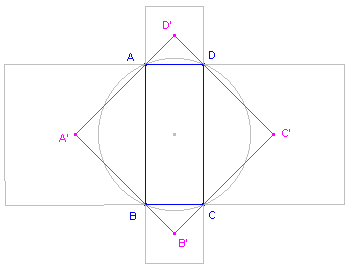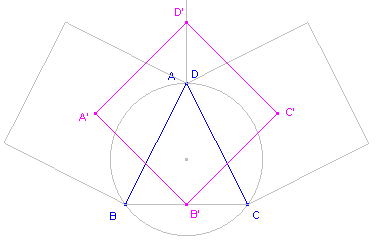vanaubel25a vanaubel25b

Zie ook Stelling 2 op deze pagina.
 
figuur 5c		  
figuur 5d
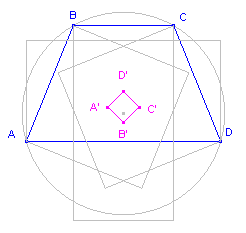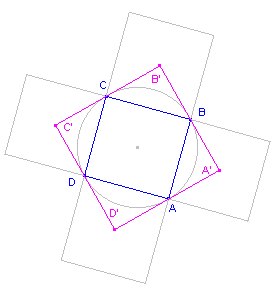vanaubel25c vanaubel25d

4. Referenties terug
Zie hiervoor de pagina "Stelling van Van Aubel".

5. Download terug
Zie de pagina "Stelling van Van Aubel" voor het downloaden van de gebruikte Cabri-figuren.

begin pagina

[vanaubel2.htm] laatste wijziging op: 06-02-01