Constructie en stellling van Grebe

Overzicht ][ Isogonalen | Lemoine en Kiepert | Punt van Vecten | Meetkunde

0. Overzicht

Constructie van Grebe
Stelling van Grebe

1. Constructie van Grebe van het symmediaanpunt van een driehoek
Ernst Wilhelm Grebe (1804-1874, Duitsland) publiceerde in 1847 een 9 pagina's tellend artikel onder de titel "Das geradlinige Dreieck in Bezug auf die Quadrate der Perpendikel, die man von einem Punkte seiner Ebene auf seine Seiten faellen kann" (Grünerts Archiv, nr. 9; 9 pagina's).
In dat artikel bewees hij (om.) de volgende stelling:

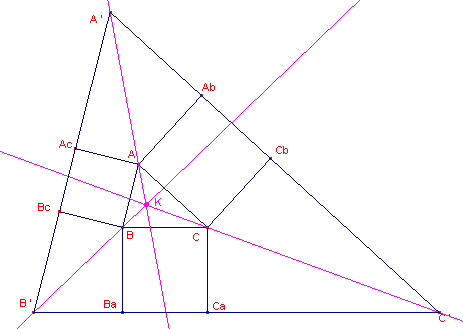
Stelling 1
Op de zijden van driehoek ABC zijn buitenwaarts vierkanten geconstrueerd (*).
De dragers van de ribben van de vierkanten die evenwijdig zijn met de zijden van driehoek ABC vormen een driehoek A'B'C' waarvan de verbindingslijnen van A', B', C' met de opvolgend A,B,C concurrent zijn.
Hun snijpunt is het symmediaanpunt (punt van Lemoine) van driehoek ABC (zie figuur 1).

(*) Zie in dit verband ook de pagina "Het punt van Vecten".

Bewijs:

figuur 1	figuur 2

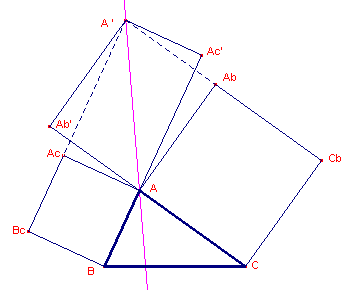Zie verder figuur 2.
Volgens Stelling 5b op de pagina "Isogonalen" geldt voor een punt op de symmediaan, dat de afstand van dat punt tot de benen van de zijden zich verhouden als die zijden.
Nu d(A', AC) = A'Ab' = AAb = AC en d(A', AB) = A'Ac' = AAc = AB.
De lijn AA' is dus symmediaan van hoek A.
Op dezelfde manier: BB' en CC' zijn symmediaan van opvolgend B en C. ¨

Opmerking
Het symmediaanpunt werd op voorstel van E. Hain ("Ueber den Grebeschen Punkt", Archiv der Mathematik und Physik, 58, 1876, pag. 84-89) naar Grebe genoemd. Daarna werd de term Grebe'sche Punkt een aantal keren in het "Jahrbuch ueber die Fortschritte der Mathematik" gebruikt door schrijvers als Dr. Schemmel (Berlijn, 1876), Prof. Mansion (Gent, 1881), Prof. Lampe (Berlijn, 1881), and Dr. Lange (Berlijn, 1885).
[einde Opmerking]

Gevolg

Stelling 2
K is (ook) het punt van Lemoine van driehoek A'B'C'.

Bewijs:
K is het centrum van vermenigvuldiging (zie ook stelling 3) van ABC naar A'B'C'. Immers de overeenkomstige zijden zijn evenwijdig en de verbindingslijnen van de overeenkomstige hoekpunten zijn concurrent.
Eigenschappen zoals die van de bissectrice en zwaartelijn, en ook die van spiegelingen worden door deze vermenigvuldiging overgedragen.
Waaruit het gestelde volgt. ¨

[einde Gevolg]

2. De stelling van Grebe

Stelling 3
De driehoeken ABC en A'B'C' zijn gelijkvormig met factor k = 1 + (a² + b² + c²) / 2S, waarbij
a, b, c de lengtes van zijden van ABC zijn en S de oppervlakte.

Bewijs:
Uit het Gevolg van Stelling 8 op de pagina "Isogonalen" volgt, dat de afstanden x, y, z van K tot de zijden a, b, c van driehoek ABC gelijk zijn aan
   x = 2aS / (a² + b² + c²)
   y = 2bS / (a² + b² + c²)
   z = 2cS / (a² + b² + c²).
Zie verder figuur 3.

figuur 3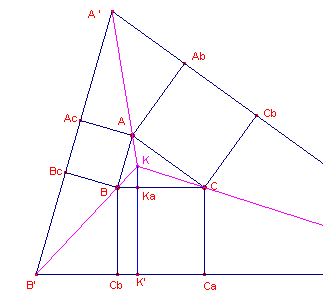

Zie stelling 2 voor het bewijs, dat de beide driehoeken gelijkvormig zijn met centrum K.
Nu is verder KK_a = x en KK' = a + x.
Voor de vermenigvuldigingsfactor k hebben we dan:
k = (a + x) / x = 1 + (a² + b² + c²)/2S
¨

[grebe.htm] laatste wijziging op: 18-11-00