De Stelling van Varignon, en meer

Zie ook de pagina "Nevencentrum, Euler-punt, Mathot-punt"

0. Overzicht

De stelling
Bewijs met vectoren
Oppervlakte van het Varignon-parallellogram
Een "toevallige" eigenschap
Ex-Varignon-vierhoek
Enkele eigenschappen
Download

1. De stelling
Of Varignon (Pierre (de?) Varignon, 1654-1722, Frankrijk) de eerste geweest is die deze stelling formuleerde (en bewees), is niet bekend; in ieder geval draagt de stelling zijn naam:

Stelling 1 - Stelling van Varignon
De middens van de zijden van een vierhoek vormen een parallellogram.

Bewijs: (zie figuur 1a)

figuur 1a		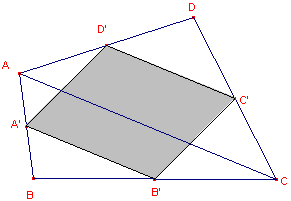De verbindingslijnstukken A'B' en C'D' zijn middenparallellen van de driehoeken ACD en ABC. Beide zijn dus gelijk aan en evenwijdig met AC. A'B'C'D' is dus een parallellogram. ¨ Klik hier voor een CabriJavapplet bij figuur 1a.
figuur 1b		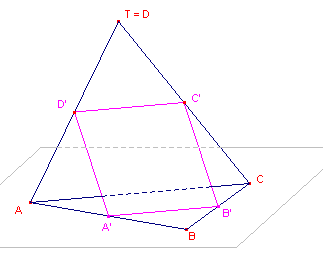Opmerkingen [1] Ook als de vierhoek niet-convex is, behoudt de stelling zijn geldigheid. [2] Ook als een hoekpunt van de vierhoek uit het vlak wordt gelicht, behoudt de stelling zijn geldigheid, ook al is ABCD dan geen vierhoek meer (zie figuur 1b). Zie ook de pagina "Scheve vierhoek" (ruimtemeetkunde). [3] A'B'C'D' heet ook wel Varignon-parallellogram (of Varignon-vierhoek) van ABCD. [einde Opmerkingen]

Gevolg
Een parallellogram is Varignon-vierhoek van een oneindig aantal vierhoeken.

Klik hier voor een illustratie daarvan met een CabriJavapplet.
[einde gevolg]

2. Bewijs met vectoren
Zie figuur 1a en 1b.
Zijn a, b, c, d de plaatsvectoren van de punten A,B,C,D. Dan is:
a' = (a + b)/2, b' = (b + c)/2, c' = (c + d)/2 en d' = (d + a)/2.
Voor de richting(svector) van A'B' hebben we dan: b' - a' = (c - a)/2.
Voor de richting(svector) van D'C' geldt dan: c' - d' = (c - a)/2.
Beide vectoren zijn dus gelijk, zodat A'B' gelijk is aan en evenwijdig met D'C'.
A'B'C'D' is dus een parallellogram.
Omdat de vectoren onafhankelijk zijn van de ligging in een vlak, is hiermee ook de ruimtelijke eigenschap (zie Opmerking 2) bewezen. ¨

3. Oppervlakte van het Varignon-parallellogram
We hebben:

Stelling 2
De oppervlakte van het Varignon-parallellogram van een vierhoek is gelijk aan de helft van de oppervlakte van die vierhoek.

Bewijs: (zie figuur 2)

figuur 2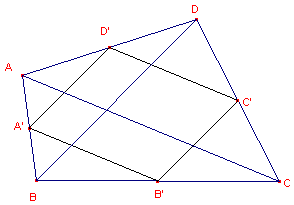

Driehoek AA'D' ontstaat door vermenigvuldiging met de factor ½ uit driehoek ABD.
De factor ½ geldt ook voor de driehoeken BB'A', CC'B' en DD'C.
De factor voor vermenigvulldiging is dus ¼. zodat
Zij p = O(ABCD).
Zij q = O(AA'D') + O(BB'A') + O(CC'D") + O(DD'A').
Dan is O(A'BC'D') = p - q ......(1)
q = ¼(O(ABD) + O(BCA) + O(BCD) + O(DAC) = ¼.2p = ½p.
Uit (1) volgt dan het gestelde. ¨

Klik hier voor een mozaïek-bewijs van stelling 2.

4. Een "toevallige" eigenschap

In de CabriJavapplet bij Stelling 1 is kunnen we zien, dat de Varignon-eigenschap ook geldt voor niet-convexe vierhoeken (zie ook figuur 3a).
Het bewijs ervan volgt eventueel ook uit Stelling 2.

figuur 3a		figuur 3b

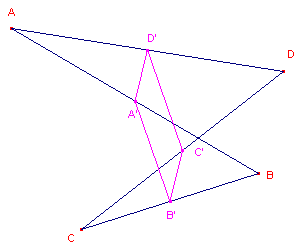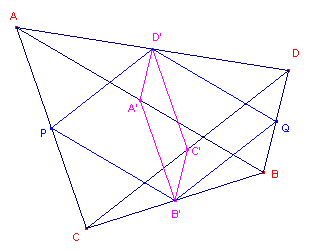ABCD is niet-convex		ACBD is convex

In figuur 3b zijn beide varianten in dezelfde figuur getekend, met hun Varignon-parallellogrammen.
Op basis hiervan kunnen we nu bewijzen:

Stelling 3
In een vierhoek zijn de beide middellijnen (*) en de verbindingslijn van de middens der diagonalen concurrent.
Het concurrentiepunt is het midden van de drie lijnstukken.
(*) Een diagonaal van het Varignon-parallellogram wordt wel middellijn van de vierhoek genoemd.

Bewijs: (zie figuur 4)

figuur 4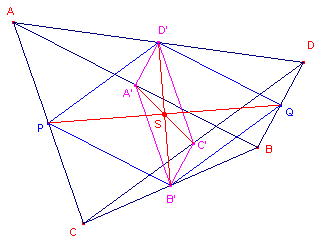

De bedoelde lijnstukken zijn de diagonalen van de beide Varignon-paralellogrammen, die diagonaal B'D' gemeenschappelijk hebben.
Ze gaan dus alledrie door het punt S.
De diagonalen n van een parallellogram delen elkaar middendoor, waarmee het gestelde is aangetoond. ¨

Klik hier voor een CabriJavapplet van Stelling 3.

Opmerkingen
[1]
De middellijn van een Varignon-parallellogram kan wellicht (en met meer recht) zwaartelijn van de vierhoek genoemd worden.
Het punt S zou dan 'het' zwaartepunt van de vierhoek zijn.
Zie in dit verband ook 'Het zwaartepunt van een veelhoek' (een Cabri-werkblad).
Zie ook de definitie van 'diacentrum' van een Varignon-parallellogram.
[2]
De lijn A'C', de verbindingslijn van de middens van de diagonalen heet ook wel Newton-lijn van de vierhoek.
Zie de pagina 'Newton-lijn'.
[einde Opmerkingen]

5. Ex-Varignon-vierhoek

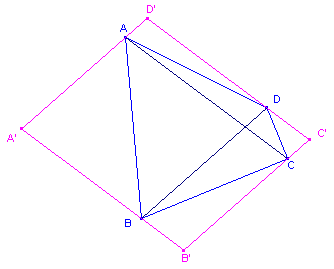
Definitie
Een ex-Varignon-vierhoek van een gegeven vierhoek is de vierhoek gevormd door de lijnen evenwijdig aan de diagonalen van die vierhoek, gaande door de eindpunten van de andere diagonaal (zie figuur 5).

figuur 5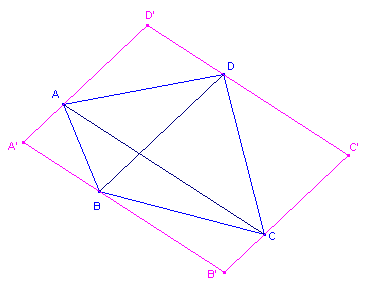

We geven zonder bewijs (het volgt immers onmiddellijk uit de definitie):

Stelling 4
De ex-Varignon-vierhoek van een willekeurige vierhoek is een parallellogram.

Enkele eigenschappen
We hebben, ook nu zonder bewijs:

Stelling 5
[1]
Als de diagonalen van een vierhoek loodrecht op elkaar staan, dan is de ex-varignon-vierhoek een rechthoek (zie figuur 6a).
[2]
Als de lengtes van diagonalen van een vierhoek aan elkaar gelijk zijn, dan is de ex-varignon-vierhoek een ruit (zie figuur 6b).

figuur 6a		figuur6b

En voorts:

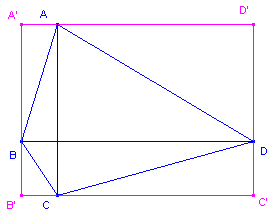Stelling 6
Van een vierhoek zijn de ex-Varignon-vierhoek en de Varignon-vierhoek gelijkstandig met gelijkvormigheidsfactor gelijk aan 2 (cq. ½).

Bewijs: (zie figuur 7)

figuur 7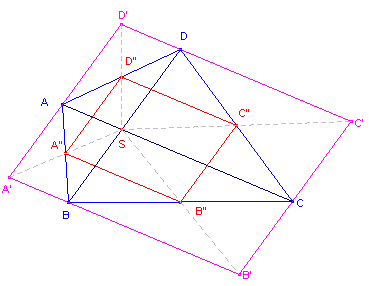

De overeenkomstige zijden van de beide parallellogrammen zijn evenwijdig.
S is het snijpunt van de diagonalen van ABCD.
AA'BS is een parallellogram, waarbij SA' door A" gaat, immers A" is het midden van AB.
SA" : SA = 1 : 2
Evenzo bewijzen we dit voor de andere hoekpunten, waaruit dan de gelijkstandigheid en de factor 2 volgt. ¨

figuur 8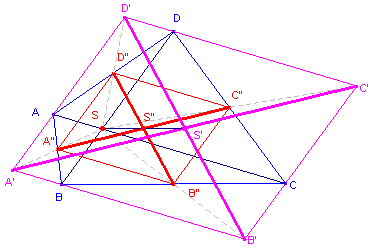

Gevolg
Van een vierhoek is het diacentrum (snijpunt van de diagonalen) van de Varignon-vierhoek het midden van het verbindingslijnstuk van het diacentrum van de vierhoek en het diacentrum van de ex-Varignon-vierhoek

Bewijs: (zie figuur 8)
S" is het midden van het lijnstuk SS'.
Dit volgt onmiddellijk uit Stelling 6 (vanwege de gelijkstandigheid van de beide Varignon-vierhoeken). ¨

6. Download
De figuren van de op deze pagina gebruikte CabriJavapplets kunnen in een bestand via deze website worden gedownload.
Klik hier om het downloaden te starten [ZIP-bestand, ca. 4Kb].

[varignon.htm] laatste wijziging op: 03-10-05