Scheve vierhoek
Overzicht ][ Overzicht stereo | Cabri
3D
Overzicht 
 |
Definitie 
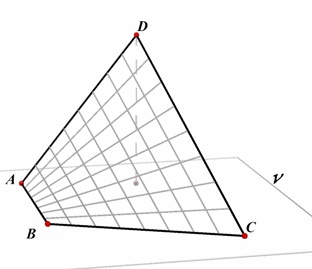
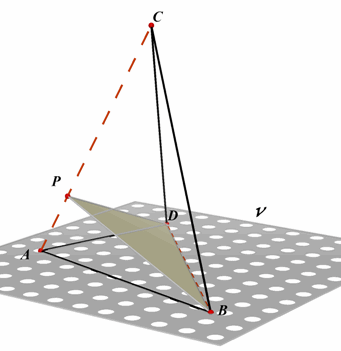
Een scheve vierhoek is een vierhoek waarvan de hoekpunten
niet in hetzelfde vlak liggen. |
N.b. We zullen in hetgeen volgt steeds uitgaan van het vlak V van driehoek ABC cq ABD.
Daarbuiten kiezen we dan het punt D cq. C.
Klik hier > < voor aan Cabri 3D applet bij deze definitie (opent in
een NieuwVenster; automatische draaiing). < voor aan Cabri 3D applet bij deze definitie (opent in
een NieuwVenster; automatische draaiing). |
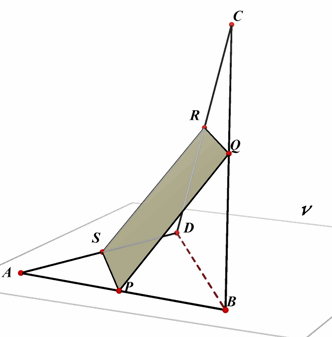 |
Stelling 1 
(Stelling van Varignon) In een scheve vierhoek zijn de middens van de
zijden de hoekpunten van een parallellogram. |
Bewijs:
P, Q, R, S zijn de middens van opvolgend AB, BC, CD, DA van de scheve
vierhoek ABCD.
In driehoek ABD is: PS //= ½ BD
In driehoek BCD is: QR //= ½ BD
Dus PS //= QR, zodat PQRS inderdaad een parallellogram is.¨
Zie ook de pagina "De Stelling van Varignon en meer"
(vlakke meetkunde). |
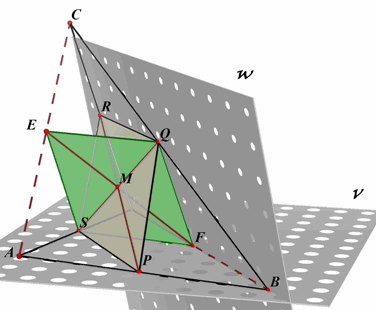 |
Stelling 2 
De drie lijnstukken die de middens van de overstaande zijden en de
middens van de diagonalen van een scheve vierhoek verbinden, gaan door hetzelfde punt en
halveren elkaar. |
Bewijs:
PQRS is een parallellogram (zie stelling 1), zodat de
lijnstukken PR en QS elkaar snijden in M en elkaar middendoor delen.
We bekijken ESFQ (met E, F midden van AC, BD.
Uit EQ //= ½ AB en FS //= ½ AB, volgt dan dat ESFQ eveneens een parallellogram is.
Ook EF gaat dus door M, waarbij M het midden is van EF.¨ |
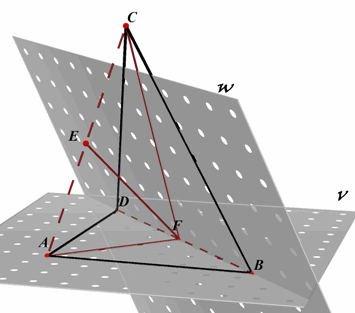 |
Stelling 3 
In een scheve vierhoek is de soms van de kwadraten van de zijden gelijk
aan de som van de kwadretn van de diagonalen, vermeerderd met vier maal de som van het
lijnstuk dat de middens van de diagonalen met elkaar verbindt. |
Bewijs:
In vlak V is AF een zwaartelijn in driehoek ABD:
AF2 = ½ AB2 + ½ DA2 - ¼
BD2 ......(i)
In vlak W is in driehoek BDC CF een zwaartelijn:
CF2 = ½ BC2 + ½ CD2 - ¼
BD2 ......(ii)
Optelling van (i) en (ii) en vermenigvuldiging met 2 geeft dan:
2( AF2 + CF2) = (AB2 + BC2
+ CD2 + DA2) - BD2 ......(iii)
In driehoek AFC is EF zwaartelijn, zodat
4 EF2 = 2(AF2 + CF2) - AC2
......(iv)
Uit (iii) en (iv) volgt het gestelde.¨ |
 |
Stelling 4 
Als de diagonalen van een scheve vierhoek elkaar loodrecht kruisen,
dan zijn de sommen van de kwadraten van de twee paren overstaande zijden gelijk. |
Bewijs:
PBD is een loodvlak op AC.
Nu is in driehoek ABP: AB2 = AP2 + BP2
en in driehoek CDP: CD2 = CP2 + DP2
Optelling geeft dan:
AB2 + CD2 = (AP2 + DP2)
+ (BP2 + CP2)
en via de stelling van Pythagoras in de rechthoekige driehoeken BPC en DPA geeft dit
AB2 + CD2 = BC2 + DA2
¨ |
Stelling 5 
Als in een scheve vierhoek de zijden elkaar loodrecht kruisen, dan
kruisen de diagonalen elkaar ook loodrecht. |
|
Bewijs:
Bekijk het viervlak ABCD. Daarin is AB_|_CD en AD_|_BC. Dan is ook AC_|_BD; dit is een
eigenschap van een orthogonaal viervlak (zie de pagina "Orthogonaal viervlak", stelling 1).¨ |
Stelling 6 
Een scheve vierhoek waarvan de sommen van de overstaande zijden gelijk
zijn, heeft een ingeschreven bol. |
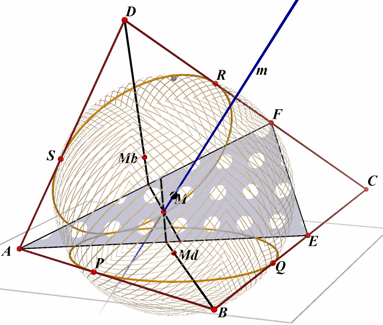 |
Onder een ingeschreven bol verstaan we in dit geval een bol die raakt aan de zijden
van de scheve vierhoek.
In feite is het zo, dat zo'n vierhoek meerdere ingeschreven bollen heeft.Voor
het bewijs van deze stelling wordt verwezen naar het artikel "Een bol die raakt
aan de zijden van een scheve vierhoek".
Dit artikel is opgenomen in een PDF-bestand.
Klik hier om dat bestand te
downloaden (PDF-formaat; ca. 346 Kb) / IE-menu: Rechtsklikken. |

[p : schevevierhoek.htm] laatste wijziging op:
06-10-2005





