Orthogonaal viervlak

[ Half-orthogonaal viervlak | Rechthoekig viervlak | Overzicht stereo | Cabri 3D ]

Definitie
Een viervlak waarvan de overstaande ribben twee aan twee loodrecht op elkaar staan, heet orthogonaal viervlak.

figuur 1

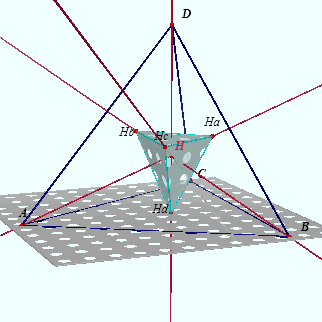Het viervlak ABCD in figuur 1 is een orthogonaal viervlak, dwz.
(1)...... AB _|_ CD
(2)...... AC _|_ BD
(3)...... AD _|_ BC
Een gevolg hiervan is dat de hoogtelijnen van het viervlak (AH_a, BH_b, CH_c, DH_d) door hetzelfde punt gaan, het hoogtepunt H van het viervlak (zie stelling 2).

Klik hier >< voor een (automatisch draaiend) Cabri 3D applet (opent in een NieuwVenster).

We bewijzen allereerst:

Stelling 1
Indien in een viervlak twee paar overstaande ribben loodrecht op elkaar staan, dan staat ook het derde paar loodrecht op elkaar.

Bewijs:

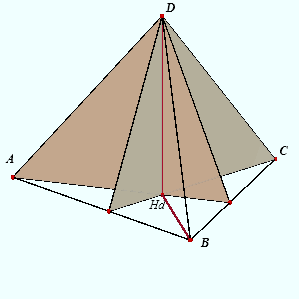In viervlak ABCD is
(1)...... BC _|_ AD
(2)...... AB _|_ CD
We moeten nu bewijzen dat AC _|_ BD.

Is nu DH_d de loodlijn uit D op vlak ABC, dan hebben we ook:
BC _|_ DH_d
Samen met (1) geeft dat: BC _|_ vlak AH_dD ......(3)
En dus, volgend uit (3): BC _|_ AH_d.

Analoog is ook AB _|_ vlak CH_dD ......(4)
En dus, volgend uit (4): AB _|_ CH_d

Het punt H_d is dan hoogtepunt van driehoek ABC. Zodat ook AC _|_ BH_d.
Maar ook AC _|_ DH_d, zodat AC _|_ vlak BH_dD, en dus
AC _|_ BD ¨

Nb.
Een rechthoekig viervlak is een bijzonder orthogonaal viervlak!

Stelling 2
In een orthogonaal viervlak gaan de hoogtelijnen op de zijvlakken door hetzelfde punt (het hoogtepunt van het viervlak).

Bewijs:

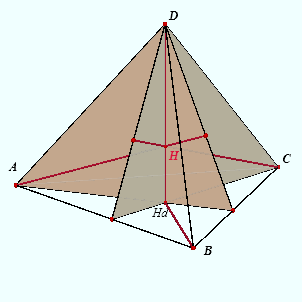Staan twee overstaande ribben loodrecht op elkaar, dan snijden de hoogtelijnen uit elk tweetal eindpunten van die ribben elkaar (eigenschap van een half-orthogonaal viervlak).
De hoogtelijnen van een orthogonaal viervlak snijden elkaar dus telkens twee aan twee., maar ze liggen niet in hetzelfde vlak.
De hoogtelijnen van een viervlak gaan dus door hetzelfde punt (het hoogtepunt H van dat viervlak). ¨

Definitie
Een viervlak waarvan de hoogtelijnen door hetzelfde punt gaan, noemt men een orthocentrisch viervlak.

Stelling 3
De verzameling orthocentrische viervlakken valt samen met de verzameling orthogonale viervlakken.

Bewijs:
(1) Een orthogonaal viervlak is orthocentrisch (zie stelling 2).
(2) De hoogtelijnen AH_a en DH_d snijden elkaar dus in het punt H. Ze liggen dan in een zelfde vlak V, waarin AD ligt.
Nu is AH_a _|_ BC en DH_d _|_ BC, zodat
BC _|_ vlak V
Dus BC _|_ AD.
Analoog voor de andere overstaande ribben. ¨

Nb.
Een rechthoekig viervlak is dus ook een bijzonder orthocentrisch viervlak!

Opmerking
Een orthogonaal viervlak heeft een aantal bijzondere eigenschappen, oa. overeenkomend met de negenpuntscirkel van de driehoek.
Zie daarvoor bijvoorbeeld het artikel "Over het Monge-punt van een viervlak en over enkele bollen", met oa. de 24-puntsbol en 12-puntsbol).
Klik hier voor een PDF-bestand (ca. 600 kB) met dat artikel. Dit bestandsformaat is te lezen met Adobe^® Reader.
Klik hier >< om Adobe Reader, indien gewenst, te downloaden.
[einde Opmerking]

[p : orthogviervlak.htm] laatste wijziging op: 19-10-2008