Rechthoekig viervlak

[ Overzicht stereo | Cabri 3D ]

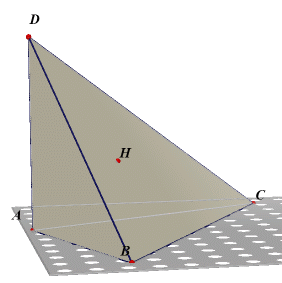
Definitie
Een rechthoekig viervlak (soms ook recht viervlak) is een viervlak waarvan de drie in één hoekpunt samenkomende ribben twee aan twee loodrecht op elkaar staan.

Nb.
Een rechthoekig viervlak is dus een bijzonder orthogonaal (orthocentrisch) viervlak!

Klik hier >< voor een Cabri 3D applet van een rechthoekig viervlak (opent in een NieuwVenster; automatisch draaiend).

Gevolg
Staan de drie in A samenkomende ribben BA, CA, DA loodrecht op elkaar, dan is het punt A het hoogtepunt van het viervlak.
[einde Gevolg]

Hulpstelling
Staan de lijnen BA, CA, DA twee aan twee loodrecht op elkaar, dan zal een willekeurig lijn PA met de lijnen BA, CA, DA hoeken b, c, d maken zodanig dat:
cos² b + cos² c + cos² d = 1

Bewijs:

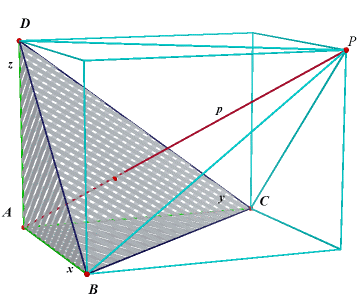Het viervlak is aangevuld tot een recht blok, waarvan P één van de hoekpunten is.
We stellen: BA = x, CA = y, DA = z en PA = p.

Nu is in de in B rechthoekige driehoek ABP:
cos(PA,BA) = cos b = x / p.
In driehoek ACP is cos c = y / p.
In driehoek ADP is cos d = z / p.
Zodat
cos² b + cos² c + cos² d = (x² + y² + z²) / p² = 1
immers p is de lengte van de lichaamsdiagonaal PA van het recht blok.¨

Stelling
In een rechthoekig viervlak is de som van de kwadraten van de oppervlakten van de (drie) rechthoekige zijvlakken gelijk aan het kwadraat van de oppervlakte van het scheefhoekige zijvlak.

Bewijs:
H is de projectie van A op het vlak BCD.
De standhoek op BC is de hoek AD'D. Stel deze gelijk aan r.
Dan is ook DAH = r.
Stellen we hoek(HA, BA) = p en hoek(HA, CA) = q.

Wegens de projectie van BCD op BCA is nu: Opp(BCA) = cos r . Opp(BCD)
Projectie van BCD op BAD geeft: Opp(BAD) = cos p . Opp.(BCD)
Projectie van BCD op ACD geeft: Opp(ACD) = cos q . Opp(BCD)
Volgens bovenstaande hulpstelling is dan: cos² p + cos² q + cos² r = 1
of
Opp²(BAD) + Opp²(ACD) + Opp²(BCA) = Opp²(BCD)¨

Gevolg
Stellen we AH = h en BA = b, CA = c, DA = d, dan is (vanwege cos p = h /a ,...): 1 / h² = 1 / b² + 1 /c² + 1 /d²
[einde Gevolg]

Opmerking
Bovenstaande stelling is het ruimtelijk analogon van de stelling van Pythagoras.
[einde Opmerking]

[p ; rechthviervlak.htm] laatste wijziging op: 29-08-2005