Koordenvierhoeken: Nevencentrum, Euler-punt, Mathot-punt

Overzicht  ][  Koordenvierhoeken | Varignon | Meetkunde

Overzicht terug

  1. Een enkele eigenschap van een willkeurige vierhoek
  2. Het nevencentrum van een koordenvierhoek cabrisignal

          Referenties

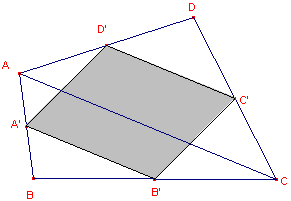
1. Een enkele eigenschap van een willekeurige vierhoek terug

Stelling 1
[1]
(Varignon) De middens van de zijden van een vierhoek vormen een parallellogram.
[2]
In een vierhoek zijn de beide middellijnen (*) en de verbindingslijn van de middens der diagonalen concurrent.
Het concurrentiepunt is het midden van de drie lijnstukken.
(*) Een diagonaal van het Varignon-parallellogram wordt wel middellijn van de vierhoek genoemd.
varig1a nevenc1
Stelling 1.1 Stelling 1.2

Voor het bewijs van Stelling 1.1 en Stelling 1.2 zie de pagina "De stelling van Varignon, en meer", daar opvolgend als Stelling 1 cabrisignal en Stelling 3 cabrisignal.

Opmerking
Het punt S, het snijpunt van de drie lijnen in Stelling 1.2, heet het zwaartepunt (van de hoekpunten) van de vierhoek.
[einde Opmerking]

2. Het nevencentrum van een koordenvierhoek terug

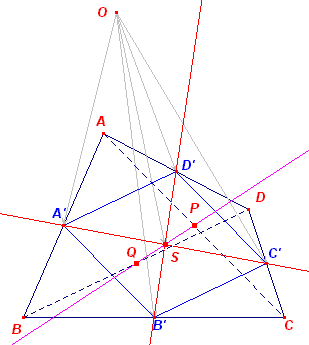
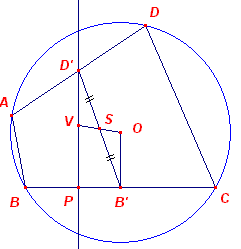
Stelling 2
De loodlijnen uit de middens van de zijden van een koordenvierhoek op de overeenkomstige overstaande zijde zijn concurrent in een punt V
Het punt V heet het nevencentrum van de koordenvierhoek (ook wel Mathot-punt, naar Jules Mathot (Mathesis, 1901, p.25-26; zie Stelling 3).

Opmerking
Hieronder (als een Gevolg van Stelling 3) zullen we aantonen, dat het nevencentrum van de koordenvierhoek samenvalt met het Euler-punt van die vierhoek.
[einde Opmerking]

Bewijs:

nevenc2 nevenc2b O is het omcentrum van ABCD. B' en D' zijn de middens van BC en DA.
Het zwaartepunt S van ABCD is het midden van B'D' (zie Stelling 1.2).
Het spiegelbeeld V van O is S ligt dus op de loodlijn D'P uit D' op BC, immers D'P // OB' en dus is OS = SV.
Maar dit geldt dan voor elke loodlijn uit elke midden, immers de positie van S is onafhankelijk van de betreffende loodlijn
Waaruit het gestelde direct volgt. ¨

Opmerking
In Engelse literatuur wordt het punt V anticenter genoemd.
[einde Opmerking]
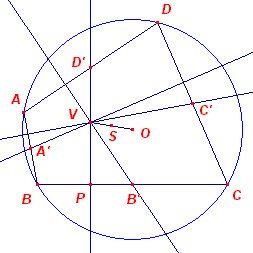
Gevolg
De lijn door het midden van een een diagonaal loodlrecht op de andere diagonaal gaat eveneens door het nevencentrum.

Bewijs:

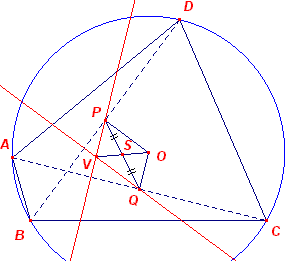nevenc2c PV _|_ AC, maar ook OQ _|_ AC, zodat
PV // OQ
Evenzo is ook QV // OP.
PVQO is dus een parallellogram, waarvan S het het snijpunt is van de diagonalen (volgens Stelling 1.2 en Stelling 2). ¨
Definitie
Een driehoek met drie van de vier hoekpunten van de koordenvierhoek als hoekpunt heet diagonaaldriehoek.
.
Stelling 3 (Jules Mathot, Mathesis, 1901, pp. 25-26)
De verbindingslijnen van een hoogtepunt van een diagonaaldriehoek van een koordenvierhoek met het 'overblijvende' hoekpunt van de koordenvierhoek zijn concurrent en delen elkaar middendoor.

Bewijs:

figuur a figuur b
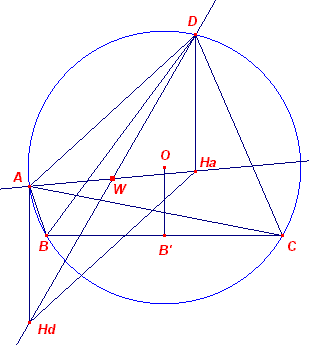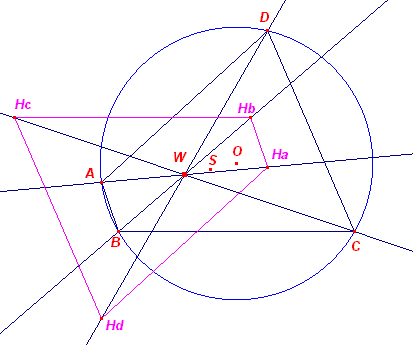nevenc3 nevenc3b
Zie figuur a hierboven.
Ha is het hoogtepunt van diagonaaldriehoek BCD.
Hd is het hoogtepunt van diagonaaldriehoek ABC.
De lijnen AHd en DHa staan beide loodrecht op BC, en zijn dus evenwijdig.
Volkgens een bekende eigenschap van de hoogtelijnen van een driehoek is:
Het bovenste hoogtelijnstuk is gelijk aan 2 maal de afstand van het omcentrum van de driehoek naar de zijde waarop die hoogtelijn staat.
Zodat AHd = 2 OB' = DHa.
AHdHaD is dus een parallellogram, waarin AHa en DHd diagonalen zijn met snijpunt W.
AHa deelt dus DHd middendoor.
Evenzo wordt DHd ook door de lijnen BHb en CHc middendoor gedeeld.
Waaruit het gestelde direct volgt. ¨
 
Gevolg 1
Zijn Ha, Hb, Hc, Hd hoogtepunten van de diagonaaldriehoeken van koordenvierhoek ABCD, dan is HaHbHcHd congruent met ABC

Bewijs:
In figuur a hierboven is het punt Ha het beeld van A bij een vermenigvuldiging met -1 tov. het punt W.
Analoog geldt dat voor de punten Hb, Hc, Hd en B, C, D.
Waaruit het gestelde volgt. ¨

Klik hier >Animatie< voor een CabriJavapplet die eea. illustreert.

Opmerking
Bovenstaande is op de pagina "Koordenvierhoeken" (Stelling 2 aldaar) vanuit een ander uitgangspunt (namelijk via Euler-cirkels) eveneens aangetoond.
Het punt W wordt daar, op basis van die uitgangspunten, het Euler-punt van de koordenvierhoek genoemd.
[einde Opmerking]

Gevolg 2
Het Euler-punt en het nevencentrum van een koordenvierhoek vallen samen.

Bewijs:
De vierhoeken ABCD en HaHbHcHd hebben op basis van de congruentie (zie Gevolg 1) omcirkels met gelijke straal. Het punt W is dus het beeld van het punt O bij vermenigvuldiging met -1 tov. het punt S, het zwaartepunt van ABCD (zie figuur b hierboven).

Referenties terug

N. Altshiller Court, College Geometry, Barnes & Noble, 1925
Pat Ballew (UK), Cyclic Quadrangles / website
Darij Grinberg (D), The Euler point of a cyclic quadrilateral; toegankelijk als ZIPped PS-file via diens de website
R. Honsberger, Episodes in 19th and 20th Century Euclidean Geometry, MAA, 1995
D. Klingens, Het nevencentrum van een koordenvierhoek (artikel, april 2008, PDF-formaat)
Webpagina "Koordenvierhoeken" (deze website)
Webpagina "De Stelling van Varignon, en meer" (deze website)

begin pagina
[p:nevencentr.htm] laatste wijziging op: 19-04-08