Newton-lijn van een vierhoek

Overzicht  ][  Meetkunde | Cabri

Zie ook de pagina "De stelling van Varignon, en meer".
Zie ook de pagina "De Newton-lijn (2)" (met stelling van Gauss-Bodenmiller en stelling van Steiner)

Overzicht terug

  1. Gnomon-theorema en volledige vierzijde
  2. De Newton-lijn van een vierhoek cabrisignal
  3. Raaklijnenvierhoek
         Stelling van Newton cabrisignal

Referenties
Download

1. Gnomon-theorema en volledige vierzijde terug
We noemen allereerst een stelling uit de Elementen van Euclides (Boek I, het gnomon-theorema).

Propositie I-43
In elk parallelogram zijn de complementen van de parallelogrammen om de diagonaal aan elkaar gelijk.
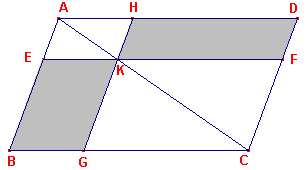propI33-6
Opmerking
Euclides geeft een parallellogram ABCD soms aan met parallellogram AC (dus alleen via een aanduiding van de diagonaal).

Er geldt nu in parallellogram AC (met S als oppervlaktefunctie):
   S(BK) = S(KD)

Klik hier voor het bewijs van deze propositie.

We kunnen Propositie I-43 gebruiken bij het bewijs van

Stelling 1
De middens van de diagonalen van een volledige vierzijde zijn collineair.

Eerste bewijs:
Zie voor de definitie van een volledige vierzijde de pagina "Volledige vierzijde en dubbelverhouding".

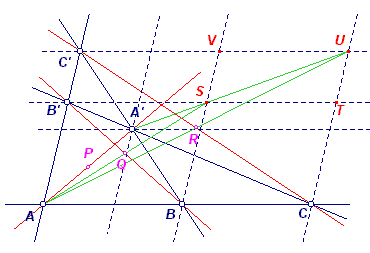volvier1 In nevenstaande figuur zijn ABC, AB'C', A'BC', A'B'C de zijden van de volledige vierzijde. AA', BB', CC' zijn dan de diagonalen van de vierzijde.
P, Q, R zijn de middens van AA', BB', CC'.

We tekenen een aantal lijnen evenwijdig met twee van de zijden van de volledige vierzijde.
Volgens Prop I-43 is dan:
S(AA') = S(A'V)
S(AA') = S(A'T)
zodat S(A'V) = S(A'T)
A' ligt daardoor op de lijn SU.
De middens van AA' (dit is het punt P), AS, AU zijn collineair.

AU en CC' delen elkaar middendoor, en ook AS en BB' delen elkaar middendoor.
Waaruit dus volgt, dat P, Q, R collineair zijn. ¨

Tweede bewijs:

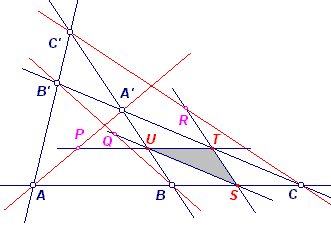volvier2 S, T, U zijn opvolgend de middens van BC, A'C, A'B.
We hebben nu
   TU /\ AA' = P
   US /\ BB' = Q
   ST /\ CC' = R
Duidelijk is nu, dat P, Q, R de middens zijn van AA', BB', CC' (middenparallellen).
Zodat:
   PT / PU = AC / AB
   QU / QS = B'A' / B'C
   RS / RT  = C'B/C'A'
Nu is AB'C' een transversaal van driehoek A'BC.
Volgens de stelling van Menelaos is dan: AC/AB . B'A'/B'C . C'B/C'A' = 1

Zodat ook
   PT/PU . QU/QS . RS/ST = 1
En... P, Q, R liggen op de zijden van driehoek STU. Zodat PQR een transversaal is van STU.
P, Q, R zijn dus collineair. ¨

Definitie
De lijn PQR heet de Newton-lijn van de volledige vierzijde (naar Isaac Newton, 1642-1727, Engeland).

Opmerking
Volgens F.G.-M. [zie 1, pag. 536] is Stelling 1 afkomstig van Gauss, in 1810 (Johann Carl Friedrich Gauss, 1777-1855, Duitsland).
Daarom wordt de lijn ook de Gauss-lijn van de volledige vierhoek genoemd.
[einde Opmerking]

2. De Newton-lijn van een vierhoek terug

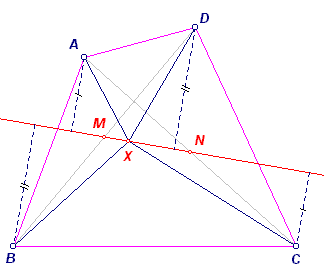
Stelling 2
Bij een vierhoek ABCD (niet zijnde een parallellogram) is de meetkundige plaats van de punten X met de eigenschap
   S(XAB) + S(XCD) = S(XBC) + S(XAD)
een rechte lijn door de middens van de diagonalen. Hierbij is S de oppervlaktefunctie.
(Pierre-Léon ANNE, geboren in 1806 te Rouaan, overleden in 1850 te Parijs [zie 1, pag. 767])

Klik hier >Animatie< voor een CabriJavapplet bij Stelling 2.

Bewijs:
Nb. Ook in dit bewijs is S de oppervlaktefunctie; d is de afstandsfunctie.

volvier3 M,N zijn de middens van de diagonalen.
Zij X een (willekeurig) punt op  MN.
Bekijk XNC en XNA. Hierin is AN = NC, zodat S(XNC)=S(XNA).
Met XN als gemeenschappelijke basis blijkt d(A,MN) = d(C,MN).
Evenzo vinden we d(B,MN)=d(D.MN).
De oppervlaktes van driehoeken die een basis hebben op MN met toppen A,C en B,D, verhouden zich dus als die bases.
   S(XAB) = S(AMB) + S(AMX) + S(BMX)
   S(XCD) = S(DMC) - S(DMX) - S(CMX)
En... S(AMX) = S(CMX), en ook SBMX) = S(DMX), zodat
(1)............ S(XBC) + S(XAD) = S(AMB) + S(CMD)
Op dezelfde manier vinden we:
(2)............ S(XBC) + S(XAD) = S(AMD) + S(CMB)

AMB, AMD hebben gelijke basis (DM = BM) en dezelfde top; zodat
   S(AMB) = S(AMD)
En zo ook
   S(CMD) = S(CMB).
We vinden dan uit (1) en (2): S(XAB) + S(XCD) = S(XBC) + S(XAD), en dit is het eerste deel van het bewijs van de stelling.
De uitdrukking S(XAB) + S(XCD) = S(XBC) + S(XAD) wordt wel Anne-conditie genoemd.

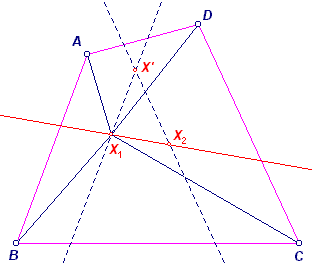volvier3b Tweede deel.
Zij X een punt buiten MN, dat aan de Anne-conditie voldoet. Voor het punt X1 op MN dat het snijpunt is van MN met de lijn door X' // AB geldt dan ook de Anne-conditie. Evenzo voor het punt X2 op MN dat het snijpunt is van MN met de lijn door X' // CD.
Dit kan alleen maar als die beide lijnen evenwijdig zijn; zodat AB // CD. Een en ander leidt dan (ook met punten X3 en X4 ontstaan als snijpunten van MN met lijnen door X' evenwijdig met CD en DA) tot een parallellogram ABCD. En dat was uitgesloten!

Waarmee de Stelling 2 bewezen is. ¨
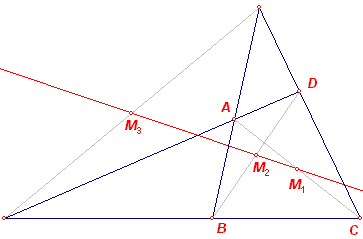volvier9 Opmerkingen
[1]
Indien het punt X buiten de vierhoek gelegen is, moet tekenwisseling (+ wordt -) plaats vinden.
[2]
Uit (1), en ook uit (2) volgt, dat
   S(XBC) + S(XAD) = S(AMD) + S(CMB) = constant
[3]
Zie de figuur hiernaast.
Beschouwen we de vierhoek als een volledige vierhoek, dan ligt het derde midden (M3) uiteraard ook op de bedoelde meetkundige plaats.
[einde Opmerkingen]

Ook nu geven we als definitie:

Definitie
De lijn door de middens van de diagnalen van een vierhoek heet Newton-lijn van die vierhoek.

We hebben nu verder:

Stelling 3
Het snijpunt van de verbindingslijnen van de middens van de overstaande zijden van een vierhoek ligt op de Newton-lijn van die vierhoek.

Bewijs:

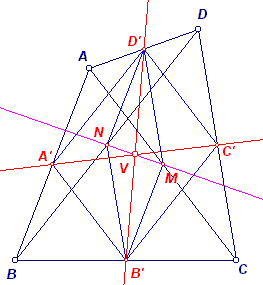volvier4 In de figuur hiernaast is de lijn MN de Newton-lijn van ABCD.
A'B'CD' is de Varignon-vierhoek (parallellogram) van ABCD.
Maar MD'NB' is de Varignon-vierhoek van ACBD.
Het midden van A'C' en B'D' (het punt V) valt dus samen met het midden van MN.
V ligt dus op MN. ¨

Opmerking
Op de pagina "De stelling van Varignon" is Stelling 3 eveneens bewezen.
Op die pagina staat ook een CabriJavapplet die Stelling 3 illustreert.
[einde Opmerking]

3. Raaklijnenvierhoek terug

Definitie
Een raaklijnenvierhoek is een vierhoek waarvan de zijden raken aan een cirkel. Deze cirkel heet ingeschreven cirkel (incirkel) van de raaklijnenvierhoek.
.
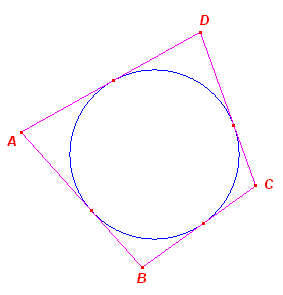volviervijf
Stelling 4
Van een raaklijnen vierhoek zijn de sommen der overstaande zijden gelijk. En omgekeerd.

Bewijs:

De raaklijnstukken uit de hoekpunten zijn twee aan twee aan elkaar gelijk.
Daaruit volgt direct dat AB + CD = BC + DA.

Het bewijs van de omgekeerde stelling is wat minder voor de hand liggend.
We onderscheiden drie gevallen:
1) a > b
2) a < b
3) a = b
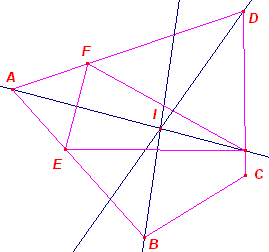volvier6 1) a > b. Uit a + c = b + d volgt a - b = d - c. Zodat d > c.
We laten nu zien, hoe de incirkel van ABCD geconstrueerd kan worden.
Kies op a = AB het punt E zo, dat BE = b
Kies op d = DA het punt E zo, dat DF = c.
Nu is AE = a - b en AF = d - c, zodat AE = AF.
De driehoeken AEF, BCD, DFC zijn dus gelijkbenig. De bissectrces van de tophoeken zijn de middelloodlijnen van de zijden van DEF. en gaan door één punt I. Dit punt ligt evenver van de zijden a, d, en van a,b  en van c, d. Het ligt dus evenver van de vier zijden. De vierhoek heeft dus een ingeschreven cirkel.

2) Deze constructie is analoog aan die van 1).
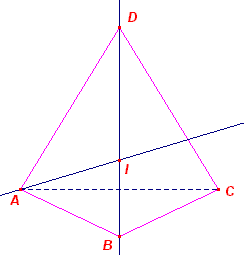volvier6b 3) Als a = b, dan is ook c = d. We hebben dan een vlieger. Het middelpunt van deze vierhoek ligt op diagonaal BD en op de bissectrice van hoek A.

Waarmee het gestelde is aangetoond. ¨
Stelling 5 terug
In een raaklijnenvierhoek ligt het middelpunt van de incirkel op de Newton-lijn van de raaklijnenvierhoek.
(Stelling van Newton)

Bewijs:

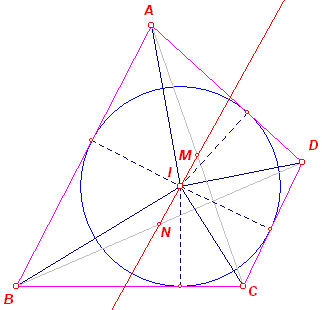volvier7 Voor het punt I (het middelpunt van de incirkel, met straal r) geldt:
S(IAB) = ½ r a, S(ICD) = ½ r c
S(IBC) = ½ r b, S(IDA) = ½ r d
Nu is
S(IAB) + S(ICD) = ½ r (a + c)
en
S(IBC) + S(IDA) = ½ r (b + d)
Wegens a + c = b + d is dus voldaan aan de Anne-conditie van Stelling 2. Het punt I ligt dus op de Newton-lijn van ABCD. ¨

Opmerking
Stelling 5 is een bijzonder geval van de volgende stelling:
De meetkundige plaats van de middelpunten van kegelsneden die ingeschreven zijn in een gegeven vierhoek, is een rechte lijn die gaat door de middens van de diagonalen van die vierhoek. [3, pag. 86]
[einde Opmerking]

Klik hier >Animatie< voor een CabriJavapplet bij Stelling 5.

Gevolg terug
In een driehoek gaat de verbindingslijn van het midden van een zijde en het midden van het verbindingslijnstuk van het overstaande hoekpunt en het raakpunt van de incirkel door het middelpunt van de incirkel.
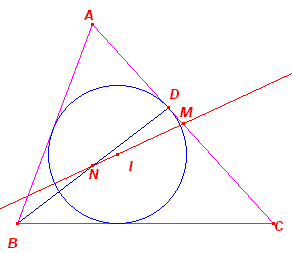volvier8 Bewijs:
(Zie ook bovenstaande applet)
Wordt het punt C in bovenstaande figuur zo gekozen, dat AD en CD in elkaars verlengden liggen, dan valt M samen met het midden van de zijde AC.
D valt dan samen met het raakpunt van de incirkel met AC. N is (nog steeds) het midden van BD.
Waaruit het gestelde volgt. ¨

Referenties terug

Zie ook de pagina "De Newton-lijn (2)"

[1]     F.G.-M: Excercises de Géométrie, Editions Jacques Gabart (reprint 1991)
[2] HEINRICH DÖRRIE: Mathematische Miniaturen , 1943 (Sändig Reprint Verlag, reprint 1999)
[3] T.E. FAULKNER, Projective Geometry, Oliver and Boyd (1949)
[4] ROGER.A. JOHNSON, Advanced Euclidean Geometry, Dover Publications (reprint 1960)

Download terug
De figuren van de CabriJavapplets op deze pagina kunnen in één bestand worden gedownload via onderstaande link.
Klik hier om het downloaden te starten (ZIP-bestand, ca. 3 kB).

begin pagina
[newtonlijn.htm] laatste wijziging op: 18-08-03