De Newton-lijn (2)
Overzicht ][ Newton-lijn (1) | Meetkunde
| Stelling 1 Voor ieder punt op de zijde van een driehoek gaat de cirkel met de "bijbehorende" hoektransversaal als middellijn door het voetpunt van de hoogtelijn op die zijde |
Bewijs:
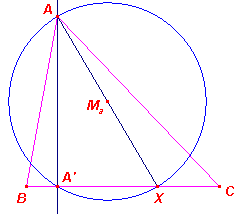 |
De cirkel op AX (met X op BC) is een Thales-cirkel. Het tweede snijpunt
A' met BC is dus het voetpunt van de hoogtelijn uit A.¨ Een Gevolg van deze stelling vinden we in Stelling 2. |
| Stelling 2 De machtlijn van de cirkels op twee hoektransversalen van een driehoek gaat door het hoogtepunt van die driehoek. |
Bewijs:
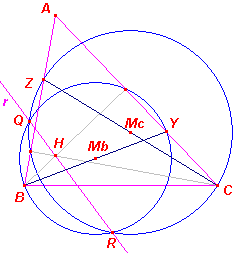 |
(verkort) De machten van het punt H ten opzichte van beide cirkels zijn
gelijk. ¨ Opmerking De in de Opmerking genoemde Stelling 8 staat hieronder als Stelling 3. |
| Stelling 3 Het hoogtepunt van een driehoek is het machtpunt van de drie cirkels op hoektransversalen door de hoekpunten van die driehoek. |
Alternatief bewijs:
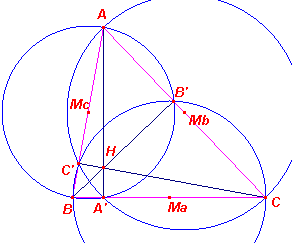 |
De cirkels van de cirkelbundel die door A en A' gaat (AA') is de
machtlijn van die bundel), hebben alle een A-ceviaan (hoektransversaal) als middellijn.
Twee van die cevianen zijn AB en AC. De cirkels op AB, AC en BC hebben twee aan twee de
hoogtelijnen van ABC als machtlijn. H is dus hun machtpunt. H is dus eveneens machtpunt voor elk drietal "ceviaan-cirkels". ¨ Klik hier > |
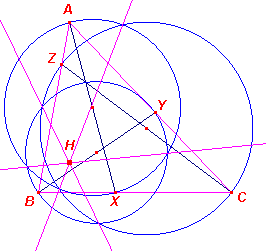 |
Opmerking Of de cevianen al dan niet concurrent zijn, is dus in Stelling 3 niet van belang (zie de hiernaast staande figuur). De eigenschap van Stelling 3 geldt dus onder meer voor de bijzondere lijnen in de driehoek (zoals bissectrices en zwaartelijnen) en voor andere concurrente cevianen. [einde Opmerking] |
2. Van driehoek naar
(volledige) vierhoek ![]()
We bewijzen nu:
| Stelling 4 Is de lijn XYZ een transversaal van driehoek ABC (X op BC, Y op CA, Z op AB), dan behoren de ceviaancirkels (AX), (BY), (CZ) tot dezelfde cirkelbundel. |
Bewijs:
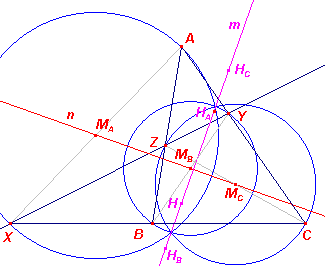 |
Allereerst merken we op, dat de hoogtepunten van de driehoeken ABC, AYZ,
BZX, CXY niet samenvallen. In Stelling 3 hebben we gezien, dat H (het hoogtepunt van ABC) het machtpunt is van de cirkels (AX), (BY), (CZ). Bekijken we nu AYZ. Op de zijden daarvan liggen de collineaire punten X, B, C. Het hoogtepunt van AYZ, HA, heeft (eveneens) gelijke machten tov. de cirkels (AX), (BY), (CZ). Dus, analoog redenerend voor de andere genoemde driehoeken, geldt dat de drie cirkels de hoogtepunten van de vier driehoeken als machtpunt hebben. Dit kan alleen maar als de machtlijnen die bedoelde machtpunten bepalen, samenvallen. De hoogtepunten zijn dus collineair. Waaruit volgt, dat de centralen van de drie cirkels eveneens samenvallen zijn. De cirkels behoren dus tot de bundel die bepaald wordt door de gemeenschappelijke machtlijn en bijvoorbeeld de cirkel AA', waarbij A' het voetpunt is van de hoogtelijn uit A op BC. ¨ |
Een direct gevolg van Stelling 4 is dan:
Bewijs:
[5.1] De middelpunten van de cirkels (AX), (BY), (CZ) zijn inderdaad de
middens van de diagonalen van de volledige vierhoek BCYZ.
[5.2] Zie het bewijs van Stelling 4. ¨
Opmerkingen
[1]
Ook de Stelling van Newton - de middens van de diagonalen van een
(volledige) vierhoek zijn collineair, volgt uit Stelling 4.
Klik hier voor de Stelling van
Newton.
[2]
Zie ook de pagina "Lijn van Simson, punt
van Miquel en lijn van Steiner" in verband met Stelling 5.2.
Zie ook de pagina "Meer bijzonderheden
van de Simson-lijn".
[einde Opmerkingen]
Zie de pagina "De Newton-lijn van een vierhoek"