De lijn van Simson, het punt van Miquel en de lijn van Steiner

Overzicht ][  Simson  |  Miquel  |  Steiner  |  Meetkunde

Overzicht terug

  1. Volledige vierhoek
  2. Gevolg : Steiner-lijn van een volledige vierhoek

1. Volledige vierhoek terug
Gaan we uit van driehoek ABC en een lijn (transversaal) die de drie zijden (of hun verlengde) snijdt, dan ontstaat een figuur die we een volledige vierhoek noemen.

In figuur 1a is ABC de driehoek en is de lijn door A' (op BC), B' (op AC) en C' (op AB) de transversaal.
We kunnen de volledige vierhoek opgebouwd denken uit de volgende driehoeken
   ABC
   AB'C'
   A'BC'
   A'B'C		     figuur 1a 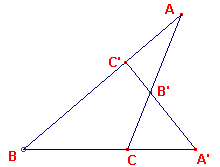imagesmisimst0 figuur 1b 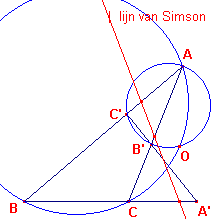imagesmisimst01

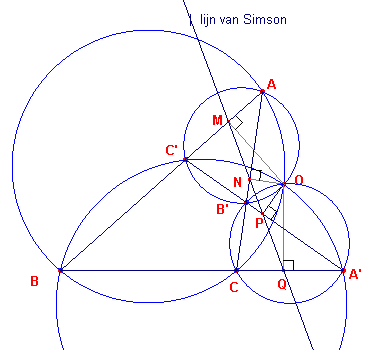
Zij nu O het van A verschillende snijpunt van de omgeschreven cirkels van driehoek ABC en AB'C'.

We kunnen nu van het punt O de lijn van Simson ten opzichte van driehoek ABC construeren (zie figuur 1b).
We doen hetzelfde voor de lijn van Simson van O ten opzichte van driehoek AB'C'.

Zie nu verder figuur 2.

figuur 2 imagesmisimst1 De lijn van Simson van O tov. ABC gaat door de punten M, N en Q.
De lijn van Simson van O tov. AB'C' gaat door de punten M, N, en P.

De punten M, N, P en Q zijn dus collineair.

Uit het feit, dat de punten N, P en Q collineair zijn, kunnen we concluderen, dat O gelegen is op de omgeschreven cirkel van A'B'C.

Uit het feit, dat de punten M, P en Q collineair zijn, kunnen we concluderen, dat O gelegen is op de omgeschreven cirkel van driehoek A'BC'.

De vier omgeschreven cirkels gaan dus door hetzelfde punt O.

Het punt O wordt in dit geval het punt van Miquel van de volledige vierhoek genoemd.

Klik hier voor een behandeling van het punt van Miquel van een driehoek op de pagina "De Stelling van Miquel".
Op deze pagina wordt bovenstaande eigenschap eveneens (maar vanuit een ander vertrekpunt) bewezen.

2. Gevolg: Steiner-lijn van een volledige vierhoek terug

figuur 3 figuur 4
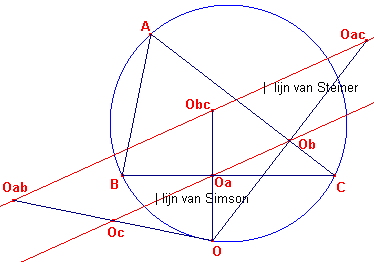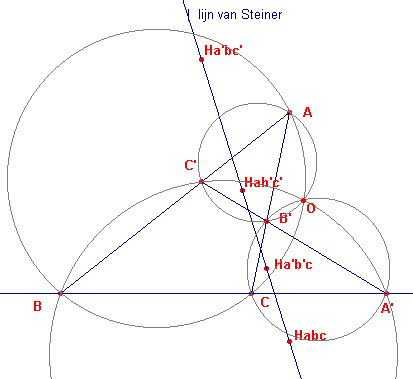imagesmisimst3 imagesmisimst2

Uit het feit, dat de lijn van Steiner uit de lijn van Simson kan worden verkregen door vermenigvuldiging met de factor 2 ten opzichte van het punt O (zie figuur 3), kunnen we nu concluderen, dat (in figuur 4):

Stelling
De hoogtepunten van de genoemde driehoeken eveneens collineair zijn.

De Steiner-lijn van ABC wordt nu wel de Steiner-lijn van de volledige vierhoek genoemd.
Zie hiervoor ook de pagina "Newton-lijn (2).

begin pagina
[misimst.htm] laatste wijziging op: 22-12-2003