Gelijkvormigheid (van drie figuren)

Overzicht  ][  Brocard-driehoeken | Meetkunde

Voor gelijkvormigheid van twee figuren zie de pagina "Bewegingen in het platte vlak"

Overzicht terug

  1. Gelijkvormigheid van drie figuren cabrisignal
         Brocard-configuratie
  2. Drie collineaire punten cabrisignal
  3. Gevolgen voor de Brocard-configuratie
  1. Download

1. Gelijkvormigheid van drie figuren terug

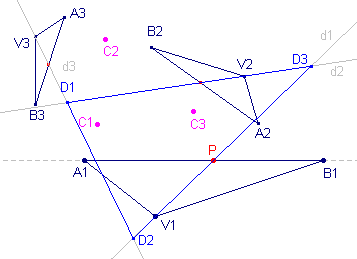gelijkv1 Zijn de figuren F1, F2, F3 direct gelijkvormig, dan kunnen we telkens twee aan twee beschouwen (F1, F2), (F2, F3), (F3, F1).
De centra van de draaivermenigvuldigingen geven we aan met Ci bij (Fj, Fk); in de tekening hiernaast is Fi = driehoek AiBiVi.
(Fj, Fk) betekent dus Fj heeft als beeld Fk.
De gelijkvormigheidsafbeeldingen zelf worden ook wel met Ci aangegeven.

We kunnen de bijbehorende rotatiehoeken vastleggen door gebruik te maken van gerichte hoeken.
Er blijkt echter een eenvoudiger manier.
Zij d1 een lijn van figuur F1 (hiernaast is d1 de lijn door V1 en P).
De opvolgende beelden van d1 zijn d2 (centrum C3) en d3 (centrum C1).
Van de driehoek gevormd door de lijnen d1, d2, d3 zijn de hoeken constant (bij variabele d1), immers de lijnen maken telkens dezelfde hoek met de zijden van de driehoeken.
We kunnen daarom ook de hoeken van driehoek D als rotatiehoeken gebruiken.

Opmerking
Driehoek D heet wel homologie-driehoek. Driehoek C heet wel gelijkvormigheidsdriehoek.
[einde Opmerking]

We hebben dus:

Stelling 1
Bij drie draaivermenigvuldigingen Ci zijn alle homologie-driehoeken gelijkvormig (eea. zoals hierboven vastgelegd, met CiCjCk = identieke afbeelding).

Klik hier > Applet< voor een CabriJavapplet ter illustratie van Stelling 1.

Ook is:

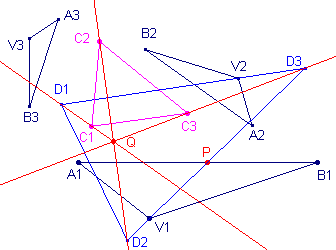
Stelling 2a
Elke homologie-driehoek is perspectief met de gelijkvormigheidsdriehoek.

Bewijs:

gelijkv2       gelijkv3 Daartoe vereenvoudigen we de "constructie" zoals in de rechter figuur hiernaast, zonder daarmee de algemene geldigheid geweld aan te doen,.
We kiezen de lijnen di langs de overeenkomstige lijnstukken AiBi (we kiezen V1 op A1B1) en we tonen aan, dat de lijnen CiDi ( met i = 1,2,3) concurrent zijn in een punt Q.

Zij | AiBi | = ai.
De gelijkvormigheidsfactoren van Ci (i = 1,2,3) zijn dan opvolgend: k1 = a3/a2, k2 = a1/a3, k3 = a2/a1.
De verhouding van de afstanden van (bijvoorbeeld) C1 tot A2B2 en A3B3 is dan k3 : k2; enz.
Volgens de Stelling van Ceva zijn de lijnen CiDi dan concurrent in een punt Q. ¨

Gevolg
Zoals opgemerkt wordt de grootte van de hoeken van driehoek D bepaald door de afbeeldingen Ci. Dit is ook het geval met de hoeken die (bijvoorbeeld) C1D1 maakt met D1D3 en D1D2; enz.
Hun som is constant (gelijk aan 180º). De verhouding van de sinussen van die hoeken is eveneens constant (gelijk aan k3 / k2).
De hoeken CiQDi zijn dus eveneens constant.
Waaruit volgt (zie rechter figuur hierboven):

Stelling 2b
De meetkundige plaats van het snijpunt van de verbindingslijnen van de hoekpunten van de gelijkvormigheidsdriehoek (het punt Q) en de homologie-driehoeken (driehoeken D) is de omcirkel van de gelijkvormigheidsdriehoek (driehoek C).
De omcirkel van de gelijkvormigheidsdriehoek heet wel gelijkvormigheidscirkel.

Klik hier > Applet< voor een CabriJavapplet ter illustratie van Stelling 2b.

Opmerking: Brocard-configuratie terug

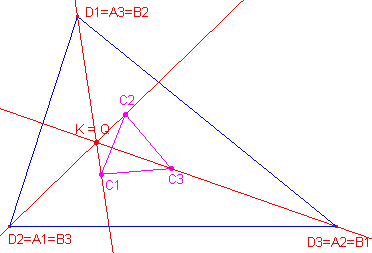gelijkv4 Vallen de lijnstukken AiBi samen met DjDk dan is Q het Lemoine-punt K van driehoek D (of dan ook van driehoek A en B).
In dit geval spreken we van de Brocard-configuratie.
De punten Ci (i = 1,2,3) zijn dan de hoekpunten van de 2e Brocard-driehoek, zijnde de gelijkvormigheidsdriehoek (bij de afbeeldingen Ci).

Zie ook de pagina "Brocard-driehoeken" en wel Stelling 5b op die pagina.

[einde Opmerking]

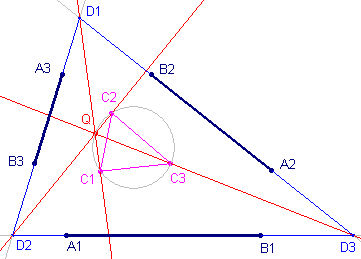
Stelling 3
De lijnen door Q evenwijdig met de zijden van de driehoeken D snijden de gelijkvormigheidscirkel in vaste punten (de invariante punten).

Klik hier > Applet< voor een CabriJavapplet ter illustratie van Stelling 3.

Bewijs:

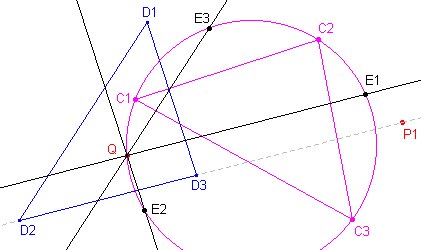gelijkv5 De bedoelde lijnen door Q maken met de zijden van de bijbehorende driehoek D vaste hoeken. Het zijn dus overeenkomstige lijnen bij de beschouwde afbeeldingen Ci.
De hoeken zijn gelijk aan die van elk ander drietal overeenkomstige lijnen.

Deze lijnen snijden de omcirkel in Ei (QE1 // D2D3; enz.).

De afstanden van C1 tot Q1E2 en Q1E3 verhouding zich nu ook weer als k3 : k2; enz.
De punten Ei zijn nu vast, omdat de hoeken EiQCj een vaste waarde hebben. ¨

Opmerkingen
[1]
De omgekeerde stelling geldt eveneens:
Zijn drie overeenkomstige lijnen (zoals op deze pagina bedoeld) concurrent, dan ligt hun snijpunt de gelijkvormigheidscirkel.
[2]
De punten E1, E2, E3 heten ook wel de invariante punten van de gelijkvormigheid(scirkel).
Hierbij is C3(E1) = E2; C1(E2) = E3; C3(E3) = E1.
Driehoek E heet wel invariante driehoek
[3]
De invariante punten zijn in de Brocard-configuratie de hoekpunten van de 1e Brocard-driehoek (zie de pagina Brocard-driehoeken; en wel paragraaf 1).
[einde Opmerkingen]

Samenvattend:

Stelling 4
De meetkundige plaats van de punten waarin drie overeenkomstige lijnen (zoals op deze pagina bedoeld) concurrent zijn, is de gelijkvormigheidscirkel.
Hierbij is het noodzakelijk dat de lijnen door de invariante punten gaan.

2. Drie collineaire punten terug

Stelling 5
De gelijkvormigheidsdriehoek is perspectief met de invariante driehoek.

Bewijs:

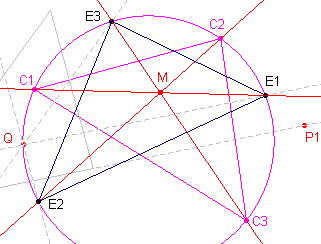gelijkv6 In de figuur hiernaast is driehoek C de gelijkvormigheidsdriehoek en driehoek E de invariante driehoek.
We zullen aantonen dat C en E perspectief zijn in het punt M.

[volgt] ¨

We zullen zien dat het punt M een rol speelt bij het collineair zijn van drie overeenkomstige punten.
Klik hier > Applet< voor een CabriJavapplet ter illustratie hiervan.
We hebben in de CabriJavapplet gezien dat:

Stelling 6
- Er zijn bij een gegeven gelijkvormigheidsdriehoek oneindig veel drietallen overeenkomstige punten die collineair zijn.
- De overeenkomstige punten liggen op drie cirkels door M en door twee van de hoekpunten van de gelijkvormigheidsdriehoek.
- De as van collineatie gaat door het punt M.

Bewijs:

[figuur] [volgt] ¨

3. Gevolgen voor de Brocard-configuratie terug

[volgt]

4. Download terug
De figuren die gebruikt zijn in de CabriJavapplets, kunnen in één bestand via deze website worden gedownload.
Klik hier om het downloadproces te starten (ZIP-bestand; ca. 13kB).

begin pagina
[gelijkvorm.htm] laatste wijziging op: 15-08-02