Generalisaties van de Simson-lijn

Overzicht ][ Lijn van Simson | Meetkunde | Cabri

Zie ook de pagina "Meer bijzonderheden van de Simson-lijn"
Zie ook de pagina "Over de Siimson-lijn van het Steiner-punt en van het Tarry-punt"

Overzicht terug
We vermelden op deze pagina enkele stellingen die generalisatie inhouden van de Simson-lijn (vooralsnog zonder bewijs).

  1. Rotatie - pseudo-Simson-lijn cabrisignal
  2. Snijding met andere zijden cabrisignal
       Collineaties cabrisignal
  3. Simson-lijnen bij een koordenvierhoek cabrisignal
       
  4. Download

1. Rotatie - pseudo-Simson-lijnen terug

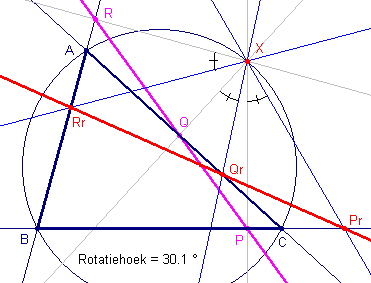simsonp1 X ligt op de omcirkel van ABC.
P,Q,R zijn de voetpunten van de loodlijnen op de zijden van ABC.
PQR is de Simson-lijn van X.
De loodlijnen worden geroteerd over een hoek a (hiernaast over 30,1º).
De snijpunten van deze beeldlijnen met de zijden zijn Pr, Qr, Rr.
Stelling 1
De punten Pr, Qr, Rr liggen weer op een lijn; deze lijn heet de pseudo-Simson-lijn van (X, a).

 

Er is sprake van een draaivermenigvuldiging die de s(X) afbeeldt op ps(X).

Klk hier Applet voor een CabriJavapplet bij het bovenstaande.

2. Snijding met andere zijden terug
We bekijken vervolgens de snijding van de loodlijnen met de andere zijden (dwz. de zijden waarop de loodlijnen niet staan).

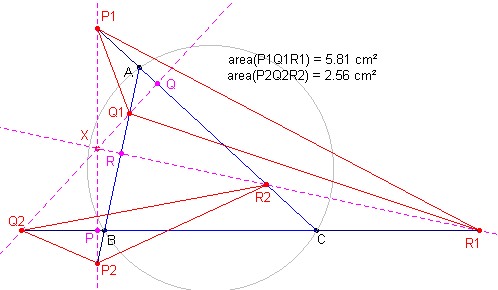
simsonp2 X is een willekeurig punt (dus niet noodzakelijk op de omcirkel).
P,Q,R zijn de voetpunten van de loodlijnen op BC, CA, AB.
P1, P2  zijn de snijpunten van XP met AC, AB.
Q1, Q2 zijn de snijpunten van XQ met AB, BC.
R1, R2 zijn de snijpunten van XR met BC, CA.
P1Q1R1 en P2Q2R2 hebben hier verschillende oppervlaktes (area).
Stelling 2
Als X op de omcirkel van ABC ligt, geldt area(P1Q1R1) = area(P2Q2R2).

Klik hier Applet voor een CabriJavapplet die Stelling 2 illustreert.

Collineaties terug
Er is een groot aantal punten waarvoor de oppervlakte van P1Q1R1 gelijk is aan 0, en ook waarvoor de oppervlakte P2Q2R2 gelijk is aan 0.
De punten P1, Q1, R1 en de punten P2, Q2, R2 zijn in dat geval dus collineair.
Het onderzoek hiernaar kan worden gedaan met onderstaande CabriJavapplets.
Klik hier Applet voor het onderzoek van P1Q1R1.
Klik hier Applet voor het onderzoek van P2Q2R2.

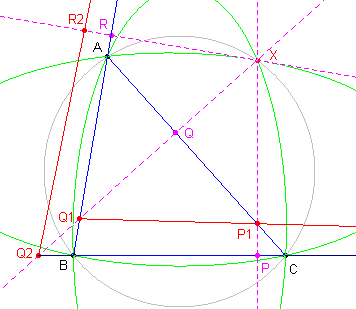simsonp3 We zien in de applets, dat de punten X waarvoor area(P1Q1R1) = 0, op een kegelsnede liggen.
Ook de punten X met area(P2Q2R2) = 0 liggen op een kegelsnede.
De punten A, B, C liggen op beide kegelsneden.
Aangezien kegelsneden elkaar in het algemeen snijden in 4 punten, is er nog een vierde punt met
area(P1Q1R1) = area(P2Q2R2) = 0
Volgens Stelling 2 ligt dit vierde punt op de omcirkel.

Klik hier Klik hier voor een CabriJavapplet hierbij.

3. Simson-lijnen bij een koordenvierhoek terug
Referentie
R.A. JOHNSON: Advanced Euclidean Geometry, Dover Publications (1960)

Er geldt:

Stelling 3
De Simson-lijnen van de hoekpunten van een koordenvierhoek bij de driehoek gevormd door de "overige" drie hoekpunten van de koordenvierhoek zijn concurrent.
.
simsonp10 Bewijs:
Voor het bewijs van deze stelling verwijzen we naar de pagina "Koordenvierhoeken".¨

Opmerkingen
[1]
In nevenstaande tekening zijn de punten H i de hoogtepunten van de "overblijvende" driehoeken (diagonaaldriehoeken); bijvoorbeeld: H1 is het hoogtepunt van driehoek A2A3A4.
Ook geldt:
H1H2H3H4 is congruent met A1A2A3A4
Merk verder op, dat de overeenkomstige zijden evenwijdig zijn.
[2]
Zie ook de pagina "Euler-cirkels".
[einde Opmerkingen]

Gaan we uit van een volledige vierhoek, dan kunnen we bewijzen:

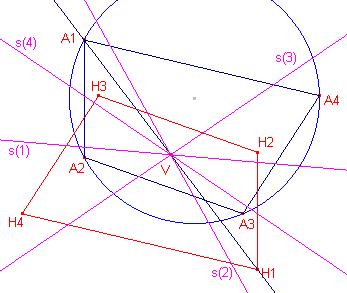
Stelling 4
[1] De voetpuntsdriehoeken van de hoekpunten van een volledige vierhoek tov. de "overblijvende" diagonaaldriehoeken zijn gelijkvormig.
(zie onderstaande linker figuur)
[2] De delen van de Simson-lijnen van vier op een cirkel gelegen punten (tov. van de drie overblijvende punten) zijn congruent:
P12P13 = P21P24 = P34P31 = P43P42 = ...
(zie onderstaande rechter figuur)

Bewijs:

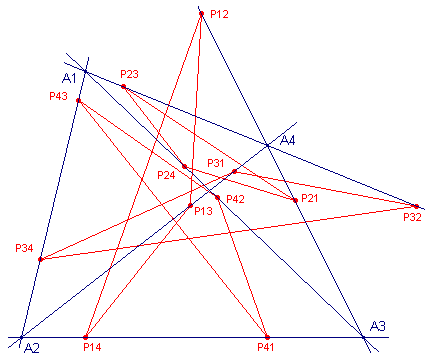simsonp11   
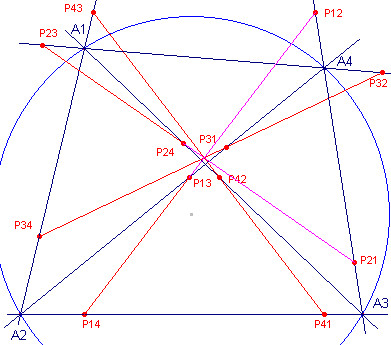simsonp11b

Het bewijs van Stelling 4.1 volgt onmiddellijk uit Stelling 2 op de pagina "De punten van Brocard".

Voor het bewijs van Stelling 4.2 kijken we naar bovenstaande rechter figuur. Het punt V is het gemeenschappelijk punt van de vier s-lijnen.
Op de pagina "Koordenvierhoeken" is reeds bewezen, dat de negenpuntcirkels van de vier diagonaaldriehoeken eveneens door V gaan (zie de figuur bij Stelling 3), en dat de stralen van de negenpuntscirkels even groot zijn (gelijk aan de helft van de omcirkel van A1A2A3A4; Koordenvierhoeken: stelling 4).
De gelijkvormigheid van de nu tot lijnstukken ontaarde driehoeken blijft natuurlijk bestaan. Het gelijkvormigheidscentrum is het gemeenschappelijk punt V.
De gelijkheid van (bijvoorbeeld) de stukken P12P14 en P41P43 volgt nu uit de vermenigvuldiging met centrum V en factor -½. ¨

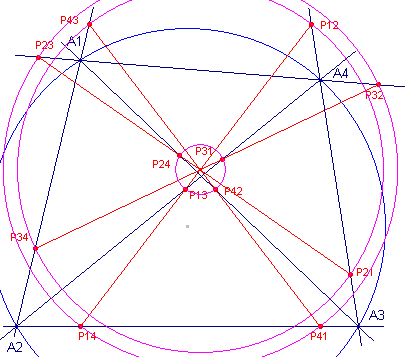simsonp12 Gevolgen
[1]
De lijnstukken met beginpunt V op de Simson-lijnen zijn per viertal gelijk:
VP14 = VP41 = VP23 = VP32 , enz.
[2]
De twaalf voetpunten van de loodlijnen liggen per viertal op concentrische cirkels (met middelpunt X). ¨

 
.
Stelling 5
Zijn Ai (i = 1,2,3,4) punten op een cirkel en P een vijfde punt op die cirkel. s(Pi) is de Simson-lijn van P tov AjAkAl .De punten Ti zijn de projecties van P op s(Pi).
Nu zijn de punten Ti collineair.

Bewijs:
In de figuren hieronder zijn de lijnen s(Pi) aangegeven met s(i). In de rechter figuur zijn niet alle objecten weergegeven.

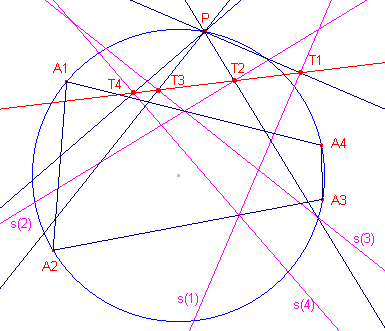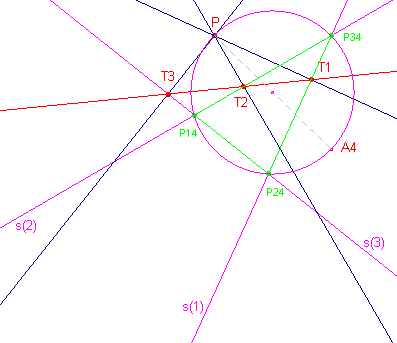simsonp13        simsonp13b

We bekijken de driehoek gevormd door de lijnen s(1), s(2), s(3). De hoekpunten daarvan zijn P34, P14 en P24.
Deze punten liggen op de cirkel met middellijn PA4.
De loodlijnen PT1, PT2, PT3 bepalen nu de s-lijn van P tov. driehoek P34P14P24.
De punten T1, T2, T3 zijn dus collineair Duidelijk is dat ook T4 op deze lijn ligt. ¨

Klik hier Klik hier voor een CabriJavapplet bij Stelling 5.

4. Download terug
De figuren die gebruikt zijn in de CabriJavapplets op deze pagina kunnen in één bestand via deze website worden gedownload.
In dit bestand is ook opgenomen de macro: SimsonLijn.mac.
Klik hier om het downloaden te starten (ZIP-bestand, ca. 8kB)

begin pagina

[simsonp.htm] laatste wijziging op: 27-12-04