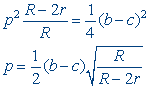Oppervlakte van voetpuntsdriehoeken, voetpuntscirkels

Overzicht  ][  Brocard-punten | Simson-lijn | Feuerbach | Meetkunde

Overzicht terug

  1. Inleiding
  2. Oppervlakte van de voetpuntsdriehoek cabrisignal
  3. Voetpuntscirkel en negenpuntscirkel
    3.1. Generalisatie van de Stelling van Feuerbach, deel 1 cabrisignal
    3.2. Generalisatie van de Stelling van Feuerbach, deel 2 cabrisignal
  4. Feuerbach-punt cabrisignal
  1. Download

1. Inleiding terug

voetp1
Definitie
De voetpuntsdriehoek van een punt P tov. van een driehoek A1A2A3 wordt gevormd door de voetpunten P1, P2, P3 van de loodlijnen uit P op de zijden (zijdelijnen) van de driehoek (het punt Pi ligt op AjAk).

Zie voor enkele eigenschappen (zoals het "voetpuntsproduct") ook de pagina "De punten van Brocard".

 

We bewijzen allereerst een hulpstelling.

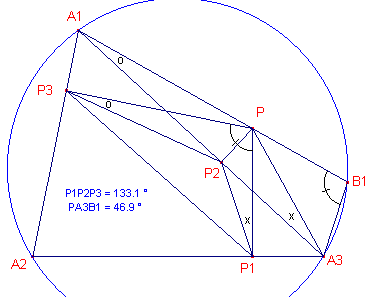
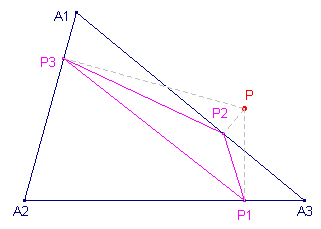
Hulpstelling 1
Is B1 het snijpunt van PA1 met de omcirkel van driehoek A, dan is in de voetpuntsdriehoek P (van punt P)
Ð P1P2P3 =  p - Ð PA3B1

Bewijs:

voetp2 Nu is:
 
P1P2P3 = 2p - (PP2P3) - (PP2P1)           ; supplement tot een volle hoek
= PP3P2 + PP1P2 + P1PP3 ; in de driehoeken PP3P2 en PP2P1
= PA1A3 + PA3A1 + P1PP3 ; PA1P3P2 en PP2P1A3 zijn kvh's
= PA1A3 + PA2A1 + (p - A2) ; A2PP1P3 is een koordenvierhoek
= PA1A3 + PA3A1 + B1 ; ook A2A3B1A1 is een kvh
= p - PA3B1 ; in driehoek A1A3B1

¨

 

2. Oppervlakte van de voetspuntsdriehoek terug

Stelling 2
De oppervlakte F van de voetpuntsdriehoek van P tov. een driehoek A is gelijk aan
voetpf1
Hierbij is O het omcentrum en R de straal van de omcirkel. Het min-teken geldt als het punt P binnen driehoek A ligt.

Bewijs: (zie bovenstaande figuur)
Onderstaand bewijs is afkomstig van Gergonne (Joseph Gergonne, 1771-1859, Frankrijk) en gepubliceerd in 1823.
In driehoek A1P3P is P2P3 / sin A1 = 2r = PA1 (sinusregel en PA1P3P2 is een kvh, met r = ½PA1 als straal van de omcirkel).
In driehoek A3P2P1 is P1P2 / sin A3 = 2r' = PA3 (sinusregel en PP2P1A3 is een kvh, met r' = ½PA3 als straal van de omcirkel).
Zodat voor de oppervlakte F van driehoek P geldt:
F(P1P2P3) = ½(P2P3)(P1P2)sin(P1P2P3) = ½(PA1)sin A1 . (PA3)sin A3 . sin(P1P2P3) ...... (1)
Nu is in driehoek PA3B1:
PA3 / sin B1 = PA3 / sin A2 = PB1 / sin PA3B1 = PB1 / sin P1P2P3 (zie Hulpstelling 1)
Zodat
PA3 . sin P1P2P3 = PB1 . sin A2 ......(2)
(2) met (1) geeft dan:
F(P1P2P3) = ½(PA1)(PB1)sin A1 . sin A2 . sin A3 ......(3)
Nu is PA1 . PB1 gelijk de macht van het punt P tov. de omcirkel. Deze macht is per definitie gelijk aan OP2 - R2 (R is straal van de omcirkel).
(3) gaat daardoor over in:
F(P1P2P3) = ½(OP2 - R2)sin A1 . sin A2 . sin A3. ¨

Gevolg
Uit de sinusregel volgt (de bekende formule): F(ABC) = abc/4R, waaruit volgt dat
voetpf3

Opmerking
Zie de pagina "Punten van Brocard" waarop op ongeveer dezelfde manier als in Stelling 2 bewezen wordt, dat de voetpuntsdriehoeken van de beide Brocard-punten dezelfde oppervlakte hebben.
[einde Omerking]

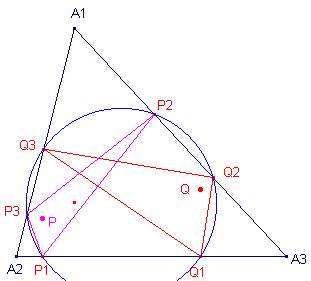
Gevolg 2.1
De meetkundige plaats van de punten waarvan de oppervlakte F van de voetpuntsdriehoek een gegeven waarde heeft, is een cirkel die concentrisch is met de omcirkel.

Bewijs:
Uit F(P1P2P3) = ½(OP2 - R2)sin A1 . sin A2 . sin A3 (zie Stelling 2) volgt dat OP constant is bij gegeven waarde van F. ¨

Klik hier Animatie voor een CabriJavapplet bij Gevolg 1.

Gevolg 2.2
De meetkundige plaats van de punten waarvan de voetpunten van de loodlijnen op de zijden van de driehoek collineair zijn, is de omcirkel van die driehoek.
De lijn van collineatie heet Simson-lijn van het punt P.

Bewijs:
In dit geval is F(P1P2P3) = 0, zodat uit F(P1P2P3) = ½(OP2 - R2)sin A1. sin A2 . sin A3 (zie Stelling 2) volgt dat OP = R
P ligt dus op de omcirkel van drie driehoek. ¨

Klik hier Animatie voor een CabriJavapplet bij Gevolg 2.

3. Voetpuntscirkel en negenpuntscirkel terug

3.1 Generalisatie van de Stelling van Feuerbach, deel 1 terug

voetp3
Stelling 3
De voetpuntscirkels van twee isogonaal verwante punten van een driehoek vallen samen.
Nb. Een voetpuntscirkel is de omcirkel van een voetpuntsdriehoek.

Opmerking
Stelling 3 is reeds bewezen op de pagina "Isogonale verwantschap", Stelling 3a.2.
En eveneens op de pagina "Cirkels van Droz-Farny"
[einde Opmerking]

Klik hier Animatie voor een CabriJavapplet bij Stelling 3.
voetp3b Zoals bekend (zie pagina Isogonale afbeeldingen, Stelling 3b) zijn de punten H (hoogtepunt) en O (omcentrum) isogonaal verwante punten.

Met Stelling 3 hebben we nu een generalisatie van (het eerste deel van) de Stelling van Feuerbach (naar Karl Wilhelm Feuerbach, 1800-1834, Duitsland):
  

Gevolg 3
De voetpunten van de hoogtelijnen en de middens van de zijden van een driehoek liggen op dezelfde cirkel.

Opmerking
De zogenoemde negenpuntscirkel is dus de voetpuntscirkel van het hoogtepunt (hoogtepuntsdriehoek) en dus ook de voetpuntscirkel van het omcentrum (centrumdriehoek).
[einde Opmerking]

3.2 Generalisatie van de Stelling van Feuerbach, deel 2 terug
We zullen hieronder ook het tweede deel van de Stelling van Feuerbach in verband brengen met voetpuntscirkels.

figuur a(4)
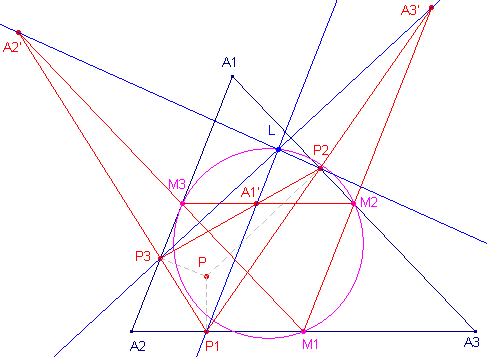
voetp4

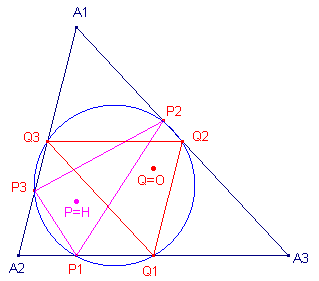
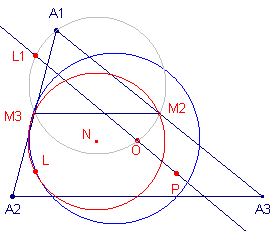
 M1, M2, M3 zijn de middens van de zijden van driehoek A.
Driehoek Pi is de voetpuntsdriehoek van het punt P tov. driehoek A.
A1' = M2M3 /\ P2P3
A2' = M3M1 /\ P3P1
A3' = M1M2 /\ P1P2
Nu geldt:
  
Stelling 4
De lijnen P1A1', P2A2', P3A3' zijn concurrent in een punt L, dat op de negenpuntscirkel ligt.

Nb.
In figuur a is de omcirkel van driehoek Mi de negenpuntscirkel.

figuur b(4)
voetp4b

  
Teneinde een duidelijker tekening te verkrijgen is in figuur b de positie van het punt P tov. de driehoek gewijzigd. Daarbij zijn er enkele onderdelen weggelaten.

Bewijs:
We beschouwen de cirkel door A1, M2 en M3.
Het punt O, omcentrum van driehoek A ligt eveneens op deze cirkel.
Dit kan worden ingezien door de cirkel met factor 2 tov. A1 te vermenigvuldigen.
De cirkel gaat dan over in de omcirkel van driehoek A.

Zij L1 het snijpunt van de lijn PO en de cirkel A1M2M3 (zie Gevolg).
A1L1O = A1L1P = 90° (Thales-cirkel)

De punten P, P2, A1, L1, P3 zijn nu concyclisch (met middellijn A1P).
Ook P1' (het spiegelbeeld van P1 in de lijn M1M2; A1P1' // A2A3) ligt op deze cirkel.

figuur c(4)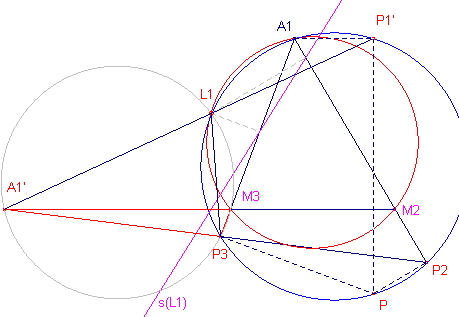
voetp4c

We tonen nu in twee stappen aan, dat de punten A1', L1 en P1' collineair zijn (zie figuur c).

(1)
L1 ligt op de omcirkel van A1M3M2; L1 ligt op de omcirkel van A1P2P3.
Deze driehoeken hebben twee zijdes met elkaar gemeenschappelijk. De Simson-lijnen van L1 tov deze driehoeken vallen dus samen (zie de lijn s(L1) in figuur c).
Maar dit is ook een Simson-lijn van driehoek A1'P3M3.
L1 ligt dus ook op de omcirkel van driehoek A1'P3M3.

(2)
Nu is A1'L1P3 = A1'M3P3 (omtrekshoeken op cirkel A1'P3M3).
A1'M3P3 = A1'M3M2 (overstaande hoeken)
A1'M3M2 + M3A1P1' = 180° (M2M3 // A1P1')
M3A1P1' + P1'PP3 = 180º (koordenvierhoek A1P1'PP3)
P1'PP3 + P3L1P1' = 180º (koordenvierhoek P1'PP3L1)

Waaruit volgt dat A1'L1P3 + P3L1P1' = 180º
De punten A1', L1, P1' zijn dus collineair.

Zij nu L het spiegelbeeld van L1 in de lijn M2M3 (zie weer figuur b).
Dan is
A1'L . A1'P1 = A1'L1 . A1'P1' (gelijke lijnstukken bij spiegeling in M2M3) ......(3)
P3P2A1 = P3PP1' (omtrekshoeken op bg P3L1P1'), zodat A1'M3P3 = A1'P2M2.
Hieruit vinden we:
A1'M3P3 ~ A1'P2M2, zodat ook A1'M3 . A1'M2 = A1'P3 . A1'P2 ......(4)
Verder is A1'L1 . A1'P1 = A1'P3 . A1'P2 ......(5)
(3), (4) en (5) geven dan
A1'L . A1'P1 = A1'M3 . A1'M2
waaruit volgt dat L op de negenpuntscirkel ligt (immers M2 en M3 liggen daarop).
Een en ander geldt mutatis mutandi ook voor de lijnen A2'P2 en A3'P3. ¨

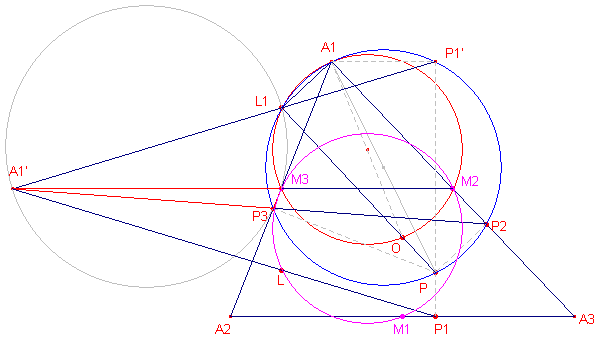
voetp5 Gevolg 4
L1 is het snijpunt van OP met de vaste cirkel A1M3M2.
Doorloopt P een vaste lijn door O, dan verander het punt L1 dus niet van plaats.
Ook het punt L verandert dan evenmin.
We hebben dan:
  
Stelling 5
Als een punt P een vaste lijn door O doorloopt, dan snijdt de voetpuntscirkel van P de negenpuntscirkel in een vast punt L.

Klik hier Animatie voor een CabriJavapplet bij Stelling 5.
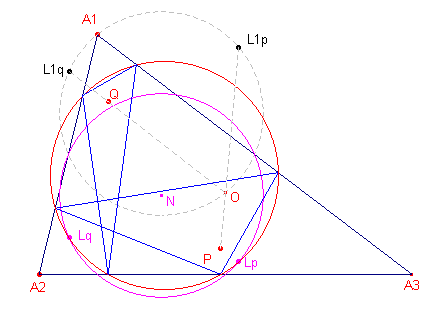voetp5b Gevolg 5
Het tweede snijpunt van de negenpuntscirkel met de voetpuntscirkel van P is afkomstig van het met P isogonaal verwante punt Q (immers P en Q hebben dezelfde voetpuntscirkel).
Willen de negenpuntscirkel en de voetpuntscirkel elkaar raken, dan moeten L1p (L1 behorend bij het punt P) en L1q (L1 behorend bij Q) samenvallen.
Zodat:
 
Stelling 6
Een nodige en voldoende voorwaarde voor het raken van de negenpuntscirkel en de voetpuntscirkel van een punt is dat het punt en diens isogonaal verwante punt collineair zijn met het omcentrum van de driehoek.

 

We kunnen nu eenvoudig uit Stelling 6 de Stelling van Feuerbach afleiden:

Stelling 7
De incirkel en de uitcirkels (ingeschreven cirkel en aangeschreven cirkels) van een driehoek raken aan de negenpuntscirkel van die driehoek.
(Karl Wilhelm Feuerbach, 1800-1834, Duitsland)

Bewijs:
Het middelpunt van de incirkel van een driehoek is isogonaal verwant met zichzelf.
De middelpunten van de uitcirkels van een driehoek zijn eveneens isogonaal verwant met zich zelf. ¨

Opmerking
Het raakpunt van incirkel en negenpuntscirkel heet Feuerbach-punt.(Kimberling: X11)
Op basis van Stelling 4 kunnen we dit punt construeren.

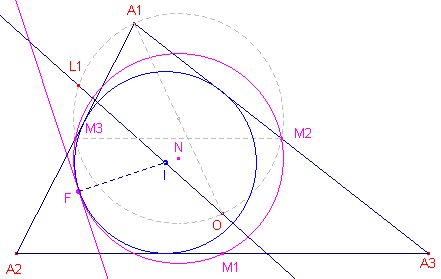voetp6 I is het middelpunt van de incirkel van driehoek A
O is het omcentrum van driehoek A.
De lijn OI snijdt de cirkel A1M3M2 in het punt L1.
Het spiegelbeeld van L1 in de lijn M2M3 is het Feuerbach-punt van driehoek A.
De gemeenschappelijk raaklijn aan de incirkel en de negenpuntscirkel (in het punt F) heet raaklijn van Feuerbach.

[einde Opmerking]

4. Feuerbach-punt terug
Hierboven is (via Stelling 7) het Feuerbach-punt van een driehoek gedefinieerd. We geven wat eigenschappen van dat punt.

Stelling 8
Het Feuerbach-punt van een driehoek is de orthopool van de lijn OI (O is omcentrum, I is incentrum van die driehoek).

Bewijs:
Op de pagina "Meer bijzonderheden van de Simson-lijn" is de orthopool van een lijn tov. van een driehoek gedefinieerd.

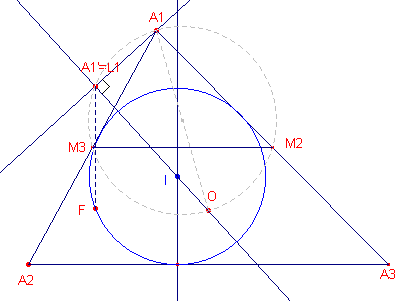voetp6b Volgens de Opmerking bij Stelling 7 construeren we het Feuerbach-punt F van driehoek A.
Uit de constructie volgt dat A1L1O = 90º (Thales-cirkel op OA1).
L1 = A1' is dus de projectie van A1 op een middellijn (zijnde OI) van de omcirkel.
Volgens Stelling 12a, Meer bijzonderheden van de Simson-lijn, is nu F de orthopool van de lijn OI.
(Die Stellinga 12a zegt, dat de orthopool de projectie is van het spiegelbeeld van de projectie van een hoekpunt in de "bijbehorende" zijde van de centrumdriehoek M1M2M3). ¨

Opmerking
Volgens Stelling 11b, Meer bijzonderheden ..., ligt de orthopool van een middellijn van de omcirkel (OI is een middellijn) inderdaad op de negenpuntscirkel (zie weer Stelling 7).
[einde Opmerking]
Stelling 9
Het Feuerbach-punt heeft tot één van de hoekpunten van de centrumdriehoek een afstand die gelijk is aan de som van de beide andere afstanden.

Klik hier Animatie voor een CabriJavapplet bij Stelling 9.

Bewijs:
De centrumdriehoek (M1M2M3) van een driehoek (A1A2A3) is de driehoek gevormd door de middens van de zijden van de gegeven driehoek

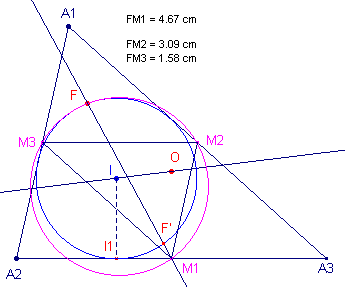voetp7 F is gelijkvormigheidspunt van de incirkel en de negenpuntscirkel.
De factor f = ½R / r = R / 2r.

Zij FM1 = p, dan is dus FF' = (2r / R) . p
Nu is (vanwege de macht van M1 tov de incirkel)):
M1F' . M1F = (M1I1)2 ......(1)
A2I1 = s - b, zodat
M1I1 = ½a - (s + b) = ½(b - c) ......(2)
M1F' = M1F - FF' = p - (2r /R)p = p(R - 2r)/R ......(3)
Uit (1), (2), (3) volgt dan:
voetpf2

Zij nu Ö( R/(R - 2r) ) = f, dan vinden we analoog q = FM2 = ½(a - c) . f en r = FM3 = ½(b - a) . f, waaruit het gestelde direct volgt. ¨

Stelling 10
- De Simson-lijn van het Feuerbach-punt F tov. de centrumdriehoek is evenwijdig met OI.
- De Simson-lijn s(F) deelt de lijnstukken FO en FI middendoor (middenparallel).

Bewijs:

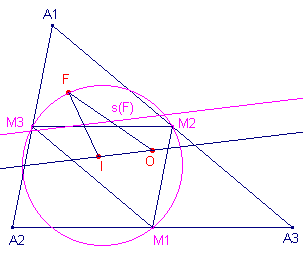voetp8 Dat S(F) // OI volgt uit het feit dat F orthopool is van OI tov. driehoek A.
Zie verder Stelling 12b, Meer bijzonderheden van de Simson-lijn.
¨

Opmerking
Zie verder ook Stelling 13.
[einde Opmerking]
Stelling 11
De Simson-lijn van het Feuerbach-punt F tov. de voetpuntsdriehoek (hoogtepuntsdriehoek) is evenwijdig met OI.

Bewijs:

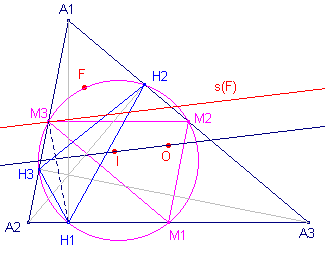voetp9 ½bg(H1M1) = H1M3M1 = H1M3M2 - M1M3M2
H1M3M2 = 180º - A1M1M2 = 180º - (A + C) = B
M1M3M2 = C
Dus: ½bg(H1M1) = B - C
Dezelfde uitdrukkingen vinden we ook voor de bogen M2H2 en M3H3 (resp C - A en A - B).
Zodat:
bg(H1M1) + bg(M2H2) + bg(M3H3) = 0
De driehoeken H en M zijn dan zogenoemde S-driehoeken (zie hiervoor de paragraaf S-driehoeken, Meer bijzonderheden ...).
Dit houdt in, dat (zie Stelling 10b, Meer bijzonderheden ...) de s-lijnen van een punt F tov. de beide driehoeken een vaste richting hebben.

Volgens Stelling 10 werd die richting voor s(F) tov. de centrumdriehoek aangegeven door OI.
Hetzelfde geldt dus voor de s-lijn van F tov. de hoogtepuntsdriehoek; maw. ook hier is s(F) // OI. ¨
Opmerking
FO en FI worden hier NIET doormidden gedeeld door s(F).
cabrisignal Zie ook de CabriJavapplet bij Stelling 13.
[einde Opmerking]

Stelling 12
De Simson-lijn van het Feuerbach-punt F tov. de Gergonne-driehoek is evenwijdig met OI.
Nb. De Gergonne-driehoek is de driehoek met raakpunten van de incirkel als hoekpunten (zie de pagina "Gergonne-punt en -driehoek").

Bewijs:

figuur a(12)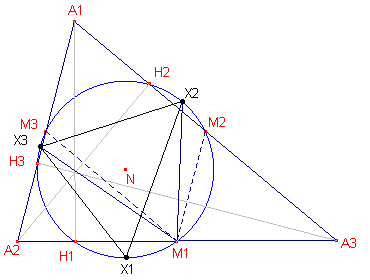
voetp10		 Zie eerst figuur a(12).
Hierin zijn X1, X2, X3 de middens van de bogen H1M1, M2M2, M3H3.
Nu is:
X3X1X2 = X3M1M2 = X3M1M3 + M3M1M2 - X2M1M2
Nu is ½bg(M3X3) = ½B - ½A, etc. (zie Stelling 11), zodat
X3X1X2 = (½B - ½A) + A - (½A - ½C) = ½B - ½C
Dus bg(X2X3) = B - C.
Analoog bg(X3X1) = C - A en bg(X1X2) = A - B, waardoor
bg(X1X2) + bg(X2X3) + bg(X3X1) = 0
Driehoek X is dus een S-driehoek van driehoek M (zie hiervoor de paragraaf S-driehoeken, Meer bijzonderheden ...).
De s-lijn van F tov. driehoek X is dus evenwijdig met OI.
figuur b(12)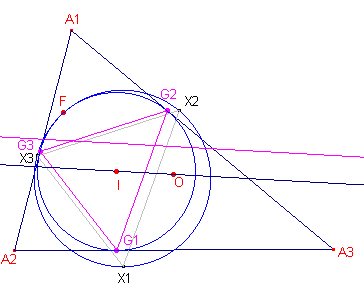
voetp10b		 Zie nu figuur b(12).
In deze figuur is driehoek G de Gergonne-driehoek van driehoek A.
Nu is driehoek G gelijkstandig met driehoek X (immers de overeenkomstige hoeken van beide driehoeken zijn gelijk). Het gelijkvormigheidscentrum is het punt F.
De s-lijn van F tov. driehoek G is dus evenwijzig met die van driehoek X; en deze laatste was weer evenwijdig met OI (zie het eerste deel van het bewijs hierboven).
Waarmee het gestelde is aangetoond. ¨

Opmerking
Zie verder ook Stelling 13.
[einde Opmerking]
.
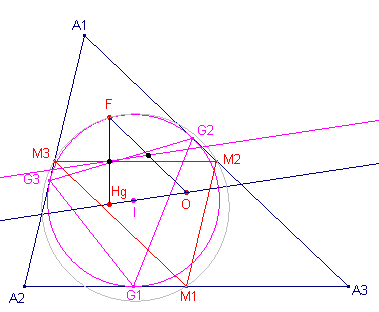voetp11
Stelling 13
De Simson-lijn van het Feuerbach-punt F tov. de Gergonne-driehoek valt samen met de Simson-lijn van F tov. de centrumdriehoek.

Bewijs:
De lijn OI is Euler-lijn van driehoek G (Gergonne-driehoek; zie Stelling 13, pagina "Uitcirkels").
Het hoogtepunt Hg van driehoek G ligt dus ook op OI (zie eventueel ook Stelling 13, pagina "Uitcirkels").
Het punt O is hoogtepunt van driehoek M.
Voor F geldt (zoals dat voor elk punt geldt), dat het midden van het verbindingslijnstuk van F met het hoogtepunt (in casu: Hg en O) op de Simson-lijn ligt.
Dus: midden van FO en midden van FHg op de Simson-lijn van F
Beide Simson-lijnen zijn evenwijdig met OI (zie Stelling 10 en Stelling 12).
Waaruit het gestelde volgt. ¨

Klik hier Animatie voor een CabriJavapplet bij Stelling 13.

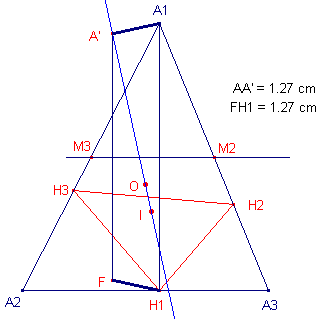voetp11b
Stelling 14
De afstanden van F tot de hoekpunten van de voetpuntsdriehoek (hoogtepuntsdriehoek) zijn gelijk aan de afstanden van de hoekpunten tot de lijn OI.

Bewijs:
Uit de constructie van het punt F (zie Stelling 8) volgt, dat A' en F symmetrisch liggen tov. de zijde M2M3 van de centrumdriehoek.
Nu is A1A'FH1 een gelijkbenig trapezium (symmetrie in M2M3, en A1H1 // A'F), zodat
FH1 = A1A', etc.
¨

 
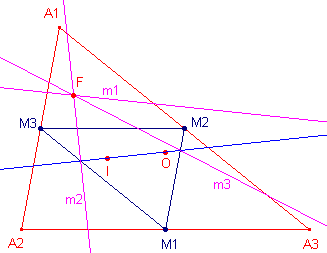voetp12
Stelling 15
De spiegelbeelden van OI in de zijden van de centrumdriehoek zijn concurrent in het Feuerbach-punt.

Bewijs:
De lijnen mi (in nevenstaande figuur) zijn de spiegelbeelden van OI in MjMk.
Zie verder Stelling 12b op de pagina "Meer bijzonderheden van de Simson-lijn"
¨

 
.
Stelling 16
Het Feuerbach-punt ligt op de cirkel door de snijpunten van de bissectrices met de overeenkomstige zijden van de driehoek
of anders geformuleerd
Het Feuerbach-punt van een driehoek ligt op de omcirkel van de ceviaandriehoek van het incentrum van die driehoek.

Bewijs:

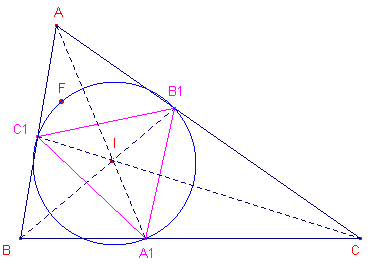voetp13 A1B1C1 is de ceviaandriehoek van het punt I (het incentrum van ABC).
Zie voor het bewijs:
L. EMELYANOV, T. EMELYANOVA: A Note on the Feuerbach Point, in: Forum Geometricorum, volume I (2001), pp. 121-124  
¨

Klik hier >Animatie< voor een CabriJavapplet bij Stelling 16.

5. Download terug
De figuren die gebruikt zijn in de CabriJavapplets, kunnen in één bestand via deze website worden gedownload.
In dat bestand is de Cabri-macro Voetpuntsdriehoek.mac eveneens opgenomen, alsmede enkele andere figuren die met het bovenstaande samenhangen.
Klik hier om het downloaden te starten (ZIP-bestand; ca. 20kB).

begin pagina
[voetpdrieh.htm] laatste wijziging op: 07-09-02