Parabool: subnormaal

Parabool: subnormaal

[ Terug naar de pagina "Parabolen: meetkundige eigenschappen en constructies" ]

We zullen bewijzen:

Stelling 5
De subnormalen van de punten van een parabool hebben een constante lengte (gelijk aan de parameter van de parabool).

Allereerst maar (een herhaling van) de definitie van subnormaal.

Definitie
De subnormaal van een punt is het lijnstuk tussen de projectie van dat punt op de as en het snijpunt van de normaal van dat punt met die as.

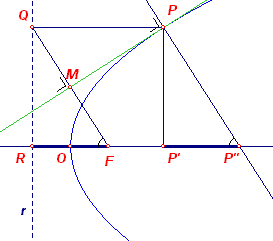In de figuur hiernaast:
- P is een punt van de parabool met brandpunt F, richtlijn r en top O;
- PM is de raaklijn in P aan de parabool;
- P'P" is de normaal van P;
- R is het snijpunt van de richtlijn r met de as OF van de parabool.

We zullen bewijzen: P'P" = FR

Klik hier >< voor een CabriJavapplet die Stelling 5 illustreert.

Opmerking:
Het lijnstuk FR heeft de lengte p en wordt de parameter van de parabool genoemd.
[einde Opmerking]

Bewijs:
PP" en FQ staan beide loodrecht op PM (de raaklijn), zodat PP" // FQ, waaruit volgt: RFQ = P'P"P.
Verder is QR = PP'. Zodat RFQ @ P'P"P (ZHH). Dus P'P" = RF.
Hetgeen bewezen moest worden. ¨

[ Terug naar de pagina "Parabolen: meetkundige eigenschappen en constructies" ]

[parab1.htm] laatste wijzigng op: 07-11-03