Driehoeksconstructie: a, b, zc

[ Driehoeksconstructies | Meetkunde | Cabri ]

[ Terug naar de pagina Driehoekconstructies ]

a, b, z_c

We behandelen hier een andere constructie dan die gegeven is op de pagina "Driehoeksconstructies".

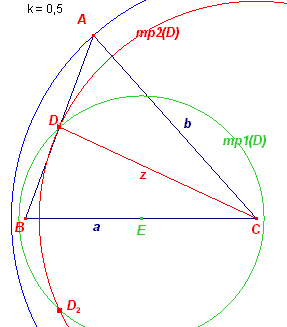B en C zijn weer in ligging gegeven, vastgelegd door het lijnstuk a.
Het punt A ligt op de cirkel met middelpunt C en straal b: (C, b).
Het punt D kan uit A worden verkregen door vermenigvuldiging met factor k = ½ en centrum B.D ligt dus op de beeldfiguur van (C, b).
Dit is een cirkel met middelpunt E (het midden van BC en straal ½b. Noem deze cirkel mp1(D)
Maar het punt D ligt ook op de cirkel met middelpunt C en straal z = z_c.
Het punt D kan dus gevonden worden als een van de snijpunten van mp1(D) en mp2(D).
A is dan het puntspiegelbeeld van B in D.

Constructie
1. We gaan uit van de in ligging gegeven punten B en C.
2. Construeer het midden E van BC.
3. Construeer de cirkel (E, ½b) - mp1(D)
4. Construeer de cirkel (C, z) - mp2(D)
5. Bepaal de snijpunten D1 en D2 van beide cirkels.
6. Bepaal het punt A als puntspiegelbeeld van B in een punt D.

[ Terug naar de pagina Driehoekconstructies ]

[abzc.htm] laatste wijiging op 25-09-03