Driehoeksconstructies: A, a - b, r en A, b + c, r

Constructies  ][  Driehoeksconstructies  |  Meetkunde  |  Cabri

Overzicht constructies terug

[ A  a - b  r ]
[ A  b + c  r ]

A, a - b , r terug  
Aa-br 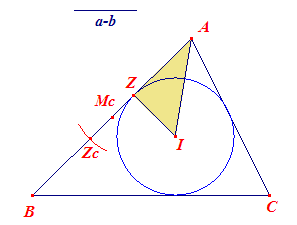Hoek A is bekend; dus ook ½A.
Z is de projectie van I op de zijde AB van driehoek ABC
Dus driehoek AZI kan worden geconstrueerd (ZHH); immers IZ = r.
Het lijnstuk ZZc (Zc is de projectie van Ic op AB) is gelijk aan a - b. Zc kan dus op AB worden gevonden met de cirkel (Z, b-c); zie Opmerking.
Zodat ook het midden Mc van AB kan worden gevonden. En daarmee dus ook het punt B (als puntspiegelbeeld van A in Mc).
Het snijpunt van de beide (tweede) raaklijnen uit A en B aan cirkel (I) is dan het punt C.

Opmerking
Voor de eigenschappen van de punten Z, Zc wordt verwezen naar:
DICK KLINGENS: Over de tritangent stralen van een driehoek. PDF-bestand (maart 2004), ca. 215 kB.

Tweede constructie
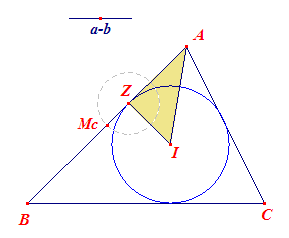Aa-br2 Zoals opmerkt is driehoek AZI te construeren. Daarin is dan:
AZ = s - a = ½(b + c - a)
Daaruit volgt ½c = AZ + ½(a - b); deze uitkomst geeft direct het punt Mc op het verlengde van AZ.
Dus het punt B is dan te construeren als het puntspiegelbeeld van A in Mc..
Het snijpunt van de beide (tweede) raaklijnen uit A en B aan cirkel (I) is dan weer het punt C.
A, b + c, r terug  
Ab+cr 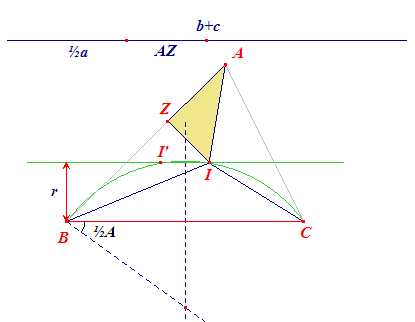Zoals opmerkt is driehoek AZI te construeren. Daarin is dan:
AZ = s - a = ½(a + b + c) - a = ½(b + c) - ½a.
Zodat:
½a = ½(b + c) - AZ
Ook de lengte van de zijde a = BC is dan bekend.
Hiermee is de constructie teruggebracht tot de constructie van [ A, a, r ].

Deze laatste constructie is ook in nevenstaande figuur uitgevoerd:
- I ligt op boog(90 + ½A, BC);
- I ligt op afstand r van BC;
- waarmee de ligging van I kan worden gevonden;
- de spiegelbeelden van de lijn BC in opvolgend BI en CI snijden elkaar dan in het punt A.

begin pagina
[p : Aa-br.htm] laatste wijziging op: 20-04-2005