Driehoeksconstructie: ha, hb, za

Theorie | Constructie ][ Driehoeksconstructies | Meetkunde | Cabri

Theorie

h_a, h_b, z_a
	We gebruiken bij de constructie de oppervlakteformule van een driehoek: Opp(ABC) = ½h_a.a = ½h_b.b en de bissectricestelling: voor het snijpunt E van de bissectrice uit C van driehoek ACD met AD geldt: AE : DE = AC : DC.

Constructie

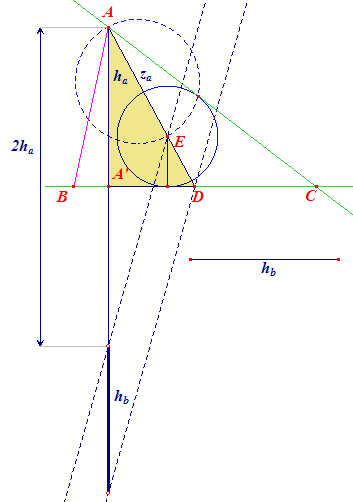Constructiebeschrijving
(Met dank aan Anneke Grünefeld-Raaphorst.)

Driehoek ADA' (met A' voetpunt van de hoogtelijn uit A op BC) is direct construeerbaar (ZZR).
Nu is (volgens de oppervlakteformule):
BC . h_a = AC . h_b
of, met x = CD, waarbij D het midden is van BC:
2x . h_a = b . h_b waaruit weer volgt: x : b = h_b : (2h_a)
Construeer nu op AD het punt E met AE : DE = (2h_a) : h_b
Het punt E ligt dan op de bissectrice van hoek C in driehoek ACD (en dus ook op die van hoek C in driehoek ABC).
AC is dan raaklijn aan de cirkel met middelpunt E en met een straal gelijk aan de afstand van E tot BC.
Hiermee vinden we het punt C op de lijn AD en via puntspiegeling van C in D ook het punt B.

[p : hahbza2.htm] laatste wijziging op: 20-12-2005