Voorwaardelijke punten met Cabri TM

Overzicht ][ Cabri | Dynamische meetkunde | Meetkunde

Overzicht

Inleiding, voorwaardelijk punt
Punten in een halfvlak, referentiepunt
Een punt binnen een driehoek
Convexe vierhoek
Toepassingen
Referenties
oa. Cabri werkblad (op deze website)

1. Inleiding, voorwaardelijk punt
Op deze pagina wordt uiteengezet hoe met behulp van het meetkundeprogramma Cabri Geometry II problemen die afhankelijk zijn van het bestaan van bepaalde punten, kunnen worden aangepakt.
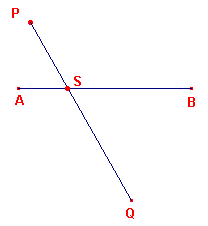
Een dergelijk probleem vinden we geïllustreerd in figuur 1.

figuur 1

We hebben een tweetal lijnstukken AB en PQ.
Het snijpunt van de lijnstukken is (hier) het punt S.
Het punt Q is een vast punt; de positie van P in het vlak kan worden gewijzigd.
We willen nu alle posities van het punt P vinden waarbij het snijpunt S bestaat.
Met andere woorden we zoeken de verzameling punten P waarvoor geldt:
het lijnstuk PQ heeft een gemeenschappelijk punt met het lijnstuk AB.

|§| Klik hier om een onderzoek naar die verzameling uit te voeren via een animatie.

Uit het via de animatie verrichte onderzoek is wellicht gebleken, dat het punt P moet worden gekozen in het in figuur 2 aangegeven (gele) deel van het platte vlak of op de randen van dat vlakdeel.
Immers ligt G op één van de randen (als deel van de halve lijn QA of als deel van de halve lijn QB) van dat vlakdeel, dan valt het punt S samen met een eindpunt van het lijnstuk (A of B), of, als P op het lijnstuk AB zelf ligt, dan vallen P en S samen.

figuur 2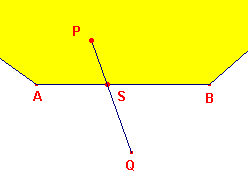

Het punt S bestaat dus niet altijd

Daarom noemen we S een voorwaardelijk punt.
Immers het punt S bestaat alleen als aan een voorwaarde voldaan is: S moet liggen in het bedoelde vlakdeel (inclusief de randen).

2. Punten in een halfvlak
(zie ook Cabri werkblad op deze website)
Het platte vlak wordt door een lijn m verdeeld in twee halfvlakken. In het platte vlak liggen ook twee punten A en B.

We stellen ons nu de vraag op welke wijze we kunnen vaststellen of beide punten in hetzelfde halfvlak of in verschillende halfvlakken liggen.

Op basis van de ligging van het spiegelbeeld van één der punten (ic. het punt B) kan worden vastgesteld of beide punten in hetzelfde halfvlak liggen.
Immers, het lijnstuk AB_S heeft met de lijn m een punt I gemeen, indien A en B in hetzelfde halfvlak liggen (zie figuur 3).
Het punt I is dus een voorwaardelijk punt. Het bestaat alléén als de punten A en B in hetzelfde halfvlak liggen.

figuur 3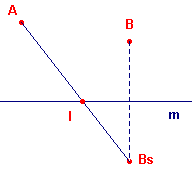

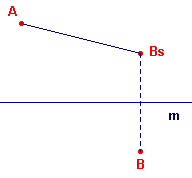We willen op basis hiervan de volgende situaties creëren:

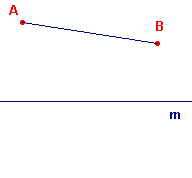
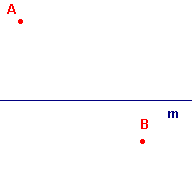
(a)	Als A en B aan dezelfde kant van m (dus in hetzelfde halfvlak) liggen, dan is het lijnstuk AB getekend; liggen A en B in verschillende halfvlakken, dan is het lijnstuk AB niet getekend (zie de beide illustraties in figuur 4).
(b)	En ook het omgekeerde van geval (a): AB is getekend dan en slechts dan als A en B aan verschillende kanten van m liggen.

figuur 4
situatie (a)

|§| Klik hier om via een animatie een (mogelijk) beter inzicht te krijgen in situatie (a).

Situatie (a)
We kunnen deze situatie bewerkstelligen door het punt I (het snijpunt van AB_S met de lijn m) op te vatten als een "voorwaardelijk punt".
Immers I bestaat (en dan is er geen lijnstuk AB) of I bestaat niet (en dan is het lijnstuk AB wel getekend).

Opmerking
In hetgeen volgt zullen we gebruikmaken van enkele constructie-opdrachten uit Cabri, zoals
- het construeren van een lijn door een punt evenwijdig met een andere lijn, en
- het construeren van het spiegelbeeld van een punt in een lijn.
We noteren deze Cabri-opdrachten als volgt:

m = Parallel(P, n) - betekenis: m is de lijn die door P evenwijding met de lijn n is getekend:
B = Reflexion(A, m) - betekenis: B is het spiegelbeeld van A in de lijn m:
Q' = Symmetry(Q, S) - betekenis: Q' is het beeld van Q bij een puntsymmetrie tov. het punt S.

Hierbij zijn Parallel (Evenwijdige lijn), Reflexion (Spiegeling) en Symmetry (Puntsymmetrie) de Cabri-opdrachten (uit de Engelse versie) die moeten worden toegepast op de daarachter tussen haakjes vermelde objecten; opvolgend zijn dit dus P, n en A, m en Q,S.

Met de Cabri-opdracht Symmetry(Q, S), met Q en S in deze volgorde, wordt dus het beeld van Q geconstrueerd met S als puntsymmetrisch centrum.
[einde Opmerking]

figuur 5
situatie (a)

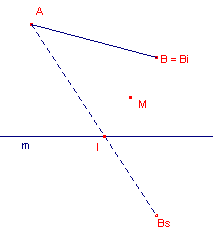We realiseren nu het gewenste door een zogenoemd referentiepunt van I te construeren, dat op dezelfde plaats ligt als het punt B (daarom geven we het aan met Bi). Het punt Bi refereert aan het bestaan van I.
Bestaat I, dan bestaat Bi; bestaat I niet, dan bestaat ook Bi niet.
We construeren Bi nu als volgt.
-  Bs = Reflexion(B, m)
-  M = Midpoint(I, B) - we bepalen het midden van het (niet-getekende lijnstuk) bepaald door I en B.
-  Bi = Symmetry(I, M)
Het gevraagde lijnstuk kunnen we nu vastleggen door A en Bi (zie figuur 5, situatie a).

Situatie (b)
|§| Klik hier om via een animatie een (mogelijk) beter inzicht te krijgen in situatie (b).

figuur 6
situatie (b)

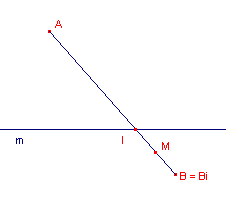Situatie (b) is eigenlijk van dezelfde orde als situatie (a). Het punt I wordt nu echter bepaald als snijpunt van AB en de lijn m.
Nu is
- M = Midpoint(I, B)
- Bi = Symmetry(I, M)
Ook nu leggen we het gewenste lijnstuk vast met A en Bi.

3. Een punt binnen een driehoek
We passen hetgeen we in de paragraaf 2 hebben gevonden toe op het volgende

Probleem
Gegeven is een willekeurige driehoek ABC en een punt M.
Er moet een punt I geconstrueerd worden -de ligging van het punt I is niet van belang-, dan en slechts dan als het punt M binnen de driehoek ligt.
|§| Klik hier om via een animatie een de voor de oplossing gebruikte voorwaardelijke punten te onderzoeken.

figuur 7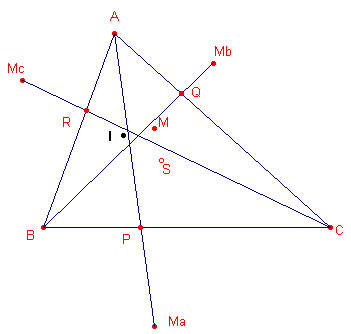

Oplossing
Het punt M ligt binnen de driehoek als tegelijk aan de volgende drie voorwaarden voldaan is:

M en A liggen aan dezelfde kant van BC
M en B liggen aan dezelfde kant van AC
M en C liggen aan dezelfde kant van AB.

Op de zijden van de driehoek bepalen we dus met de methode uit paragraaf 2 de voorwaardelijke punten P, Q en R bepaald door M_A, M_B en M_C.
M ligt dus binnen de driehoek, indien de punten P, Q en R tegelijk bestaan.

Ter constructie van het voorwaardelijke punt I merken we voorts op, dat het midden van een lijnstuk slechts bestaat als beide eindpunten daarvan bestaan.
We kiezen (dus) S als midden van PQ en I als het midden van SR (zie figuur 7).

4. Convexe vierhoek
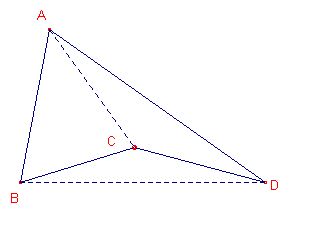
Een vierhoek heet convex als de lijnstukken die de diagonalen van die vierhoek vormen, een gemeenschappelijk punt hebben (zie figuur 8).

Het punt S, dat gedefinieerd is als het snijpunt van de lijnstukken AC en BD bestaat alleen als de vierhoek convex is.
|§| Klik hier

om via een animatie de verschillende mogelijkheden te bekijken.

We kunnen het voorwaardelijke punt S gebruiken om op een andere plaats, bijvoorbeeld op de plaats van het punt D, een tweede voorwaardelijk punt te construeren.
Zoals bekend is dit een referentiepunt; het refereert aan het (bestaan) van het eerste voorwaardelijke punt.

Omdat S voorwaardelijk is, is ook het midden M van het lijnstuk DS voorwaardelijk.

figuur 8

Gebruiken we M nu als symmetriecentrum, dan kunnen we het referentiepunt met het label (de naam van het punt) "S_m" op dezelfde positie als die van D construeren, met
S_m = Symmetry(S, M)

Eén en ander is geïllustreerd in figuur 9 (eigenlijk ook al in figuur 8 en in de animatie, waarin het label van het referentiepunt gelijk is aan "convexe vierhoek").

figuur 9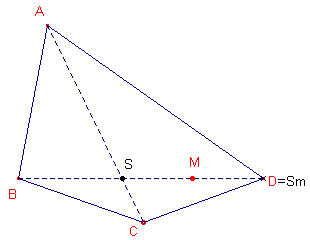

5. Toepassingen

Toepassing 1 - Kortste van twee lijnstukken
Toepassing 2 - Punt binnen of buiten een cirkel
Toepassing 3 - Zichtbare of niet zichtbare tekst (schuifknop)
Toepassing 4 - Een punt tov. drie cirkels

Toepassing 1
Gegeven zijn de lijnstukken MA en MB.
Bepaal het lijnstuk dat het kortste is.
|§| Klik hier om via een animatie kennis te maken met het probleem..

Oplossing: We gaan er eerst van uit, dat MA < MB

figuur 10
MA < MB

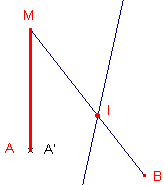De middelloodlijn van AB snijdt het lijnstuk MB in het punt I, omdat (in dit geval) M dichter bij A ligt dan bij B.
I is dus een voorwaardelijk punt. We kunnen dus op het punt A het referentiepunt van I construeren met de "naam" (label) A’. We gebruiken hierbij het midden P (niet getekend) van het lijnstuk IA; dus A' = Symmetry(I, P).
Het lijnstuk MA’ kan dan via een andere kleur (en/of dikte) het kortste lijnstuk markeren.

Als MA > MB moeten we dezelfde constructie uitvoeren, maar nu voor het punt I op MA en het referentiepunt B’ als symmetriepunt van I ten opzichte van het midden van IB.

Het probleem van het bepalen van het kleinste van twee lijnstukken heeft geen unieke oplossing.
|§| Klik hier om via een animatie de oplossing van het probleem te bekijken waarbij twee andere referentiepunten worden gebruikt.

Toepassing 2
(zie ook Cabri werkblad op deze website)
Gegeven is een cirkel met middelpunt O. Verder is er nog een punt A.
Bepaal of het punt A binnen, dan wel buiten de cirkel ligt.
|§| Klik hier om via een animatie eerst zelf te ontdekken hoe dit probleem zou kunnen worden opgelost.

figuur 11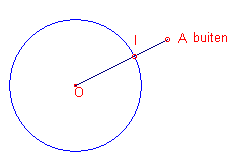

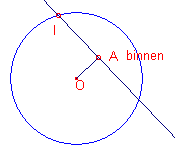Oplossing: Ligt A buiten de cirkel, dan is het snijpunt I van OA een voorwaardelijk punt (zie figuur 11, links).
We kunnen het referentiepunt A’ (we geven dit nu de naam "buiten") met behulp van I vastleggen als we het midden van P (niet getekend) van het lijnstuk IA gebruiken:
A buiten = Symmetry(I, P).

Ligt A binnen (of op) de cirkel, dan kunnen we een voorwaardelijk punt I construeren als snijpunt van de loodlijn in A op OA. Het referentiepunt A’ geven we in dit geval de naam "binnen" (zie figuur 11, rechts).

Opmerking
Zie ook de pagina "Cabri-FAQ", vraag 16 (Maximale afstand tussen twee punten), op deze website.
[einde Opmerking]

Toepassing 3
Op basis van de positie van een punt op een lijnstukje (dat we schuifknop noemen) willen we een tekst al of niet zichtbaar maken.

|§| Klik hier om via een animatie te kijken wat met deze toepassing bedoeld wordt.

Oplossing:
Bij de vaststelling of het punt "zichtbaar" in de positie "wel" of "niet" staat, kan gebruik gemaakt worden van het midden van de schuifknop.
We leggen op de middelloodlijn van de schuifknop een voorwaardelijk punt I vast via een verbindingslijnstuk tussen het punt waar we de tekst willen plaatsen en het punt "zichtbaar" (zie figuur 12).

figuur 12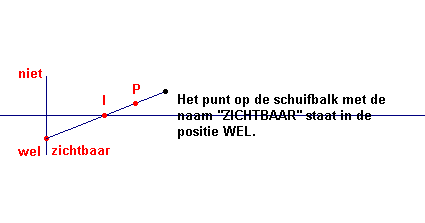

In deze figuur is I het snijpunt van de middelloodlijn en het lijnstuk tussen het punt "zichtbaar" en het vaste punt waarbij we de tekst willen plaatsen
Verder is
"Het punt op ..." = Symmetry(I, P)
Dit punt is dus het referentiepunt van het punt I.

|§| Klik hier om met een animatie de oplossing van het "tekst-probleem" nog eens helemaal in beeld te krijgen.

We maken bij de oplossing van Toepassing 3 dus weer gebruik van de ligging van twee punten in verschillende halfvlakken (die bepaald worden door de middelloodlijn van de schuifknop).
Zie hiervoor eventueel opnieuw paragraaf 2.

Toepassing 4

In figuur 13 kunnen we zien, dat het punt M binnen de drie cirkels A, B, C ligt.

Om de "status" van het punt M te bepalen ten opzichte van de drie cirkels, is gebruik gemaakt van een aantal voorwaardelijke punten en een zestal referentiepunten op een lijnstuk.
Van deze referentiepunten zien we er nu drie: inA, inB, inC.

|§| Klik hier om met een animatie de opbouw van de figuur verder te exploreren.

N.B.
In deze toepassing is oa. gebruik gemaakt van Toepassing 2, een punt binnen of buiten een cirkel.

figuur 13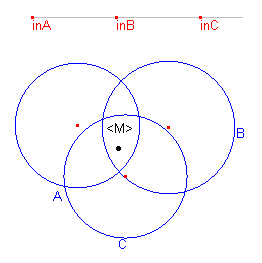

6. Referenties

Op deze website staat ook een Cabri werkblad over dit onderwerp.
Zie ook de pagina "Cabri-FAQ", vraag 16 (Maximale afstand tussen twee punten), op deze website.
Pagina's over hetzelfde onderwerp zijn te vinden op de site van abraCAdaBRI (F).
Zie verder op deze website de pagina "Boole'se functies in Cabri".

[voorwptn.htm] laatste wijziging op: 04-09-2002