Boole'se functies in Cabri TM
Overzicht ][ Cabri | Cabri-FAQ | Cabri-macro's | Meetkunde | Analyse
Zie ook de pagina "Voorwaardelijke punten"
- Inleiding
- Een voorbeeld
- Enkele Boole'se functies in Cabri
3.1. BEval0
3.2. NotBEval0
3.3. NOT(boolean)
3.4. BAND en BOR - Vergelijken van twee getalwaarden
4.1. BKleinerGelijk
4.2. BGroterGelijk
1. Inleiding 
Met Cabri is het mogelijk, deels via ingebouwd functies, deels via macro's, JA/NEE vragen
te beantwoorden.
Zo zien we in het Eigenschappen-menu:
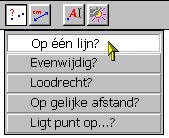
En met behulp van een macro kan bijvoorbeeld de vraag "Ligt dit punt
tussen (of op één van) twee evenwijdige lijnen?" worden beantwoord.
Klik hier >
< voor een CabriJavapplet
ter illustratie.
In de applet is een aangepaste versie van een macro met de naam VoorwPunt
gebruikt (zie Cabri-FAQ, vraag 35).
We zullen in paragraaf 2 een Cabri-functie definiëren
die (min of meer) hetzelfde gevolg heeft als de in deze applet gebruikte macro.
 |
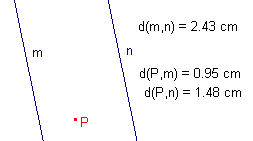Bij het beantwoorden van een vraag als "Ligt dit punt tussen
twee evenwijdige lijnen" maken we vaak gebruik van numerieke waarden. In dit geval is het antwoord op de vraag JA, als de som van de afstanden van P tot elk van de lijnen gelijk is aan de afstand tussen beide evenwijdige lijnen. Is d(m,n) ¹ d(P,m) + d(P,n), dan is het antwoord NEE. |
Het verplaatsen van een punt op het tekenblad van Cabri waarbij een punt
"precies" op een lijn komt te liggen, is schier onmogelijk (zie daarvoor CabriFAQ-17 en CabriFAQ-35).
Ook in het onderhavige geval hebben we daarmee te maken.
Vandaar dat we bij het definiëren van de functies (meestal via macro's) steeds een zekere
mate van (on)nauwkeurigheid zullen moeten incalculeren.
We bekijken nu de waarde van q in:
q = d(P,m) + d(P,n) - d(m,n)
(1) q = 0 als P tussen de evenwijdige lijnen m en n
ligt;
(2) q ¹ 0 als P niet tussen m
en n ligt.
Omdat bij het verplaatsen van het punt P de waarde van q dus (bijna) nooit
precies 0 wordt, kiezen we als nauwkeurigheid (bijvoorbeeld) 0,05.
We zeggen in Cabri dus:
q = 0 als -0,05 < q < 0,05
We bekijken in dit verband de Cabri-functie 
Opmerking
Zie voor de Cabri-functies CEIL en FLOOR
de pagina "CabriFAQ-34".
[einde Opmerking]
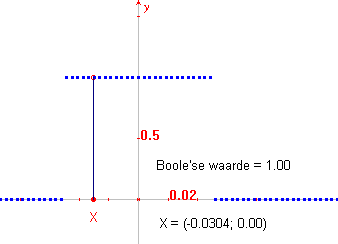
De grafiek van de functie f staat hieronder:
We zullen in Cabri de uitkomst 1 (true) van deze functie interpreteren als JA, en de
uitkomst 0 (false) als NEE.
De functiewaarden 0 en 1 noemen we Boole'se waarden (Eng. Boolean
values; naar George Boole, 1815-1864, Engeland).
We kunnen gemakkelijk nagaan, dat
(1) f(x) = 1 als -0,05 < x < 0,05
(2) f(x) = 0 als x £
-0,05 of als x ³ 0,05
En dat is precies wat we wilden bereiken:
(1) de functie f heeft als waarde 1 (true), als q = 0
(conform hetgeen we in dit geval in Cabri willen verstaan onder q = 0)
(2) de functie f heeft als waarde 0 (false), als q ¹ 0.
Klik hier >< voor een CabriJavapplet
waarin deze functie (via een macro) gebruikt wordt.
3. Enkele Boole'se
functies in Cabri
In deze paragraaf zullen we enkele functies behandelen, die betrekking hebben op de in paragraaf 1 bedoelde JA/NEE vragen.
Dit type functies noemen we Boole'se functies.
De in paragraaf 2 gebruikte functie geven we de naam BEval0
(boole's evalueren van de functievariabele op 0):
BEval0(x) = 1 als x = 0
BEval0(x) = 0 als x ¹ 0
waarbij we x in een 0.05-omgeving van 0 ook gelijk aan 0 noemen (Cabri-0?).
Het vastleggen van de macro verloopt via de volgende stappen:
1 - InvoerGetallen (typ een getal,
bijvoorbeeld 0.04)
2 - Rekenmachine
 Typ: 1-ceil( floor( 20*abs( |
 Typ vervolgens: ) ) / (1 + floor( 20*abs( |
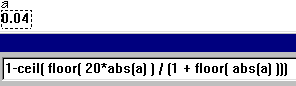 Typ tenslotte: ) ))) |
Voer de functie uit paragraaf 2 in als in bovenstaande figuren.
Selecteer in plaats van a twee keer het getal 0.04.
Klik dan op het gelijk-teken en plaats de waarde (in dit geval 1.00) op het tekenblad.
3 - Definieer vervolgens de macro:BEval0 met:
Beginobjecten: het getal 0.04
Eindobjecten: het getal 1.00
Opmerking
Om de nauwkeurigheid op te voeren kan ook een waarde van bijvoorbeeld 10 000 000
(in plaats van 20) worden gebruikt.
[einde Opmerking]
De logische ontkenning van de functie BEval0 geven we aan met NotBEval0,
zodat
NotBEval0(x) = 0 als x = 0
NotBEval0(x) = 1 als x ¹ 0
De definierende Cabri-functie hierbij is: ceil( floor( 20*abs(x) ) / (1 +
floor( abs(x) )))
De gebruikelijke logische (Boole'se) ontkenning NOT kunnen we vastleggen via
de Cabri-functie 1 - x, zodat
NOT(1) = 0
NOT(0) = 1
N.B.
Deze functie werkt, aldus gedefinieerd, niet zoals we verwachten, als we als variabele een
getal kiezen dat ongelijk is aan 0 en ongelijk aan 1.
Door de functie 1 - ABS(sign(x)) in de definitie te gebruiken
komen we wat dichter bij wat gebruikelijk is.
 |
Klik hier ><
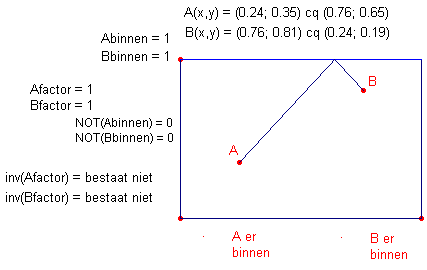voor een CabriJavapplet met een toepassing van de functie NOT(boolean). In deze applet wordt ook gebruik gemaakt van de functie 1/x, waarbij voor x = 0 (met Cabri-waarde "bestaat niet") en voor x = 1 (met waarde 1) een Boole's punt wordt geconstrueerd (zie verder ook de paragraaf Download). Met dank aan collega Valentijn Van Hootegem (Vlaanderen). Zie verder ook de pagina "Schuifbalk" |
Het kan in voorkomende gevallen handig zijn ook logische functies tot onze beschikking
te hebben die twee reële waarden Boole's evalueren op 0, waarbij dan de uitkomst wordt
bepaald door het logische AND of het logische OR van de Boole'se uitkomsten:
AND(1,1) = 1; en in andere gevallen 0
OR(0,0) = 0; en in andere gevallen 1
De functies BAND en BOR kunnen nu worden vastgelegd met
BAND(x,y) = BEval0(x) * BEval0(y)
BOR(x,y) = SIGN( BEval0(x) + BEval0(y) )
Klik hier >< voor een CabriJavapplet
die de bovenstaande functies illustreert.
4. Vergelijken van twee
getalwaarden
Willen we weten of een getal kleiner dan of gelijk aan een tweede getal
is (bijvoorbeeld bij lengtes van twee lijnstukken), dan kunnen we dat eveneens met een
Boole'se functie afhandelen.
We stellen hierbij de nauwkeurigheid weer 0.05 (wellicht dat een kleinere waarde beter zou
zijn, maar dan kunnen we de macro:BEval0 niet gebruiken).
We bekijken eerst de functie f(x) = ABS(x) + x
Voor x £ 0 geldt: f(x) = 0.
Voor x > 0 geldt: f(x) = 2x.
We hebben voor x = a - b een eenvoudig kriterium om uit te maken of a £ b. We kunnen immers gebruik maken van de functie BEval0.
Met de volgende stappen leggen we de macro vast.
1 - InvoerGetallen (typ bijvoorbeeld 5 en 12)
2 - Rekenmachine
Voer in het invoer-venster de functie ABS(a-b) + (a-b) in; zie
onderstaande figuur, waarin a = 5 en b= 12.
| figuur 4.1a | figuur 4.1b |
 |
 |
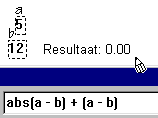En zet het Resultaat op het tekenblad (zie figuur 4.1a)
3 - macro:BEval0(2) ...... "2" betekent
hier dat het resultaat van Stap 2 moet worden geselecteerd.
De waarde van BEval0 is dan (als het goed is) gelijk aan 1 (zie figuur 4.1b).
4 - We definieren de macro:BKleinerGelijk nu met:
Beginobjecten: de getallen 5 en 12 (in deze
volgorde; zie Stap 1)
Eindobjecten: de Boole'se waarde 1.
De macro:BGroterGelijk kunnen we op dezelfde manier als
in 4.1 vastleggen.
We moeten dan de getallen (5 en 12) voor de berekening van het eerste resultaat via de
functie ABS(a-b) + (a-b) in omgekeerde volgorde selecteren: eerst a = 12 en dan
b = 5 (in Stap 2).
Bij Beginobjecten selecteren we dan weer in de
volgorde 5, 12 (in Stap 4).
Klik hier >< voor een CabriJavapplet
die de functies uit paragraaf 4 illustreert.
5.
Download
De in de applets gebruikte Cabri-figuren kunnen in één bestand via deze website worden
gedownload.
In dat bestand zijn ook enkele andere figuren opgenomen, alsmede de hierboven behandelde
macro's. Alle macro's kunnen ook worden geladen via het opgenomen Cabri menubestand Boolean.Men; hierin staan ook twee (hierboven) niet behandelde
macro's: BPunt.Mac en PuntBWaarde.Mac.
Ook zijn in het bestand enkele voorbeelden opgenomen voor het testen van eigenschappen
van figuren (parallellogram, gelijkzijdige driehoek).
Bij deze laatste is de nauwkeurigheid eveneens 0.05 (een waarde die eigenlijk te klein
is).
Klik hier >< voor een CabriJavapplet
met een toepassing van macro:BPunt en macro:PuntBWaarde.
Klik hier om het downloadproces te starten (ZIP-bestand, ca. 30kB).
Met dank aan Jean-Charles Monrocq (Collège Louise Michel, Manville-sur-Risle, Frankrijk)
[boole.htm] laatste wijziging op: