Ellips-constructies met Cabri [4b]
Constructie | Bewijs ][ Kegelsneden | Macro's voor kegelsneden | Cabri
Vorige 
Begin 
Volgende
4b. Een ellips voortgebracht via een
brandpunt en een richtcirkel
We gaan uit van een punt F en een cirkel met middelpunt M en straal a.
F ligt binnen de cirkel.
Zij nu P een punt van de cirkel.
We zoeken nu de meetkundige plaats van de punten X, waarvoor XP = XF (bij
variabele P).
Constructiestappen
- Teken een cirkel met middelpunt M en willekeurige straal (lengte gelijk aan 2a).
- Teken het punt F binnen de cirkel.
- Kies P op de cirkel.
- Bepaal het snijpunt van de middelloodlijn m van het lijnstuk PF en de lijn door P en M.
- Construeer met de functie "Meetkundige plaats" in het Constructie-menu de meetkundige plaats van X als P de cirkel doorloopt (zie figuur 4b).
| figuur 4b |  |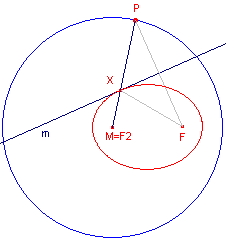
Klik hier 
voor een animatie bij deze constructie.
Bewijs
Uit de constructie (zie Constructiestappen) volgt:
XM + XF = XM + XP = MP = 2a.
Uit de gebruikelijke definitie van de ellips (zie paragraaf 0)
volgt nu, dat X op een ellips ligt. ¨
De cirkel wordt de richtcirkel van de ellips genoemd (zie ook Opmerking 1).
De straal van de richtcirkel is gelijk aan de lengte van de grote as van de ellips.
Het punt M is dus het tweede brandpunt (F2) van de ellips.
De ellips heeft een tweede richtcirkel, nl. de cirkel met middelpunt F (met straal gelijk
aan 2a).
Opmerkingen
[1]
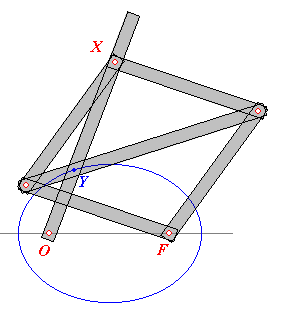
Op deze constructie is ook een stangenmechanisme gebaseerd waarmee een ellips
getekend kan worden.
 |
Via het punt F is een ruit geconstrueerd waarbij het punt X beweegbaar
is. Verschuifbaar rond X is een stang bevestigd met als andere eindpunt het punt O. Deze laatste stang heeft in het punt Y een tekenstift die binnen de diagonaalstang van de ruit heen en weer schuift, als het punt X wordt bewogen. N.B. Het punt X draait door het stangenmechanisme over een cirkel! Klik hier > Nevenstaand mechanisme wordt in de Engelse literatuur wel "Trammel van
Archimedes" genoemd. Maar of Archimedes hier iets mee te maken heeft gehad
moet ernstig worden betwijfeld. |
[2]
Zie voor een uitvoerige behandeling van enkele meetkundige eigenschappen van de
richtcirkel de pagina "Over de richtcirkel van een ellips".
[3]
De richtcirkel van een ellips kan worden gebruikt voor de constructie van de
raaklijnen uit een punt aan de ellips.
Zie de pagina "Twee raaklijnen aan een ellips".
[einde Opmerking]
Vorige Begin Volgende
[ellips4b.htm] laatste wijziging op: 02-03-2005