Ellips-constructies met Cabri [4a]

Constructie  ][  Kegelsneden  |  Macro's voor kegelsneden  |  Cabri

4a. Een ellips voortgebracht via een brandpunt en een richtlijn

We kiezen een punt F en een rechte lijn r (die niet door F gaat).
De lijn r heet richtlijn van de ellips.
We trachten nu de meetkundige plaats te bepalen van de punten X waarvoor geldt
   XF = k ^. d(X, r)
waarbij verder k < 1.
Het getal k heet de excentriciteit van de kegelsnede. Deze wordt bijna altijd aangegeven met de letter e.

We geven hieronder een globale beschrijving van de constructie (zie figuur 4).
Zij P een willekeurig punt op de lijn r.
We construeren uitgaande van P allereerst een punt Q dat gelijke afstanden heeft tot F en r.
We moeten nu op de lijn door Q evenwijdig met r een punt construeren een punt X construeren met XF = k QF = k d(Q, r).
Dit doen we met de functie "Vermenigvuldiging" uit het Afbeeldingen-menu van Cabri:
We moeten daartoe echter eerst de verhouding k vastleggen.
Om een algemeen werkende constructie te verkrijgen leggen we k vast als de verhouding tussen twee lijnstukken c en a (met c deel van a).
Vermenigvuldigen we nu het punt Q ten opzichte van F met k (met beeldpunt Q'), dan kunnen we het gezochte punt X vastleggen (op de lijn door Q evenwijdig aan r) met de cirkel (F,FQ').

figuur 4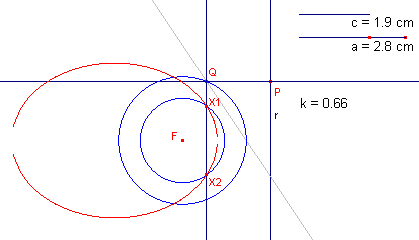

Nb.

In figuur 4 is een kortere constructie uitgevoerd: de cirkel (F, FQ) is vermenigvuldigd met k ten opzichte van het punt F.
Merk op, dat er twee punten, X₁ en X₂, uit de constructie volgen. Beide bepalen een deel van de meetkundige plaats.

Klik hier voor een animatie bij deze constructie.

Het noodzakelijke bewijs laten we achterwege.

Opmerking
Zie voor een uitvoeriger meetkundige behandeling van de richtlijn de pagina "Over de richtlijn van een ellips".
[einde Opmerking]

---

[ellips4.htm] laatste wijziging op: 02-01-2001