Ellips-constructies met Cabri [3]

Constructie  |  Bewijs  ][  Kegelsneden  |  Macro's voor kegelsneden  |  Cabri

3. Constructie als orthogonale projectie van een cirkel

Zie figuur 3a.

figuur 3a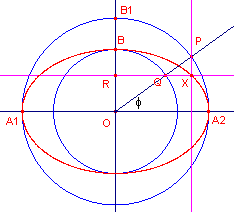

Opmerking De cirkel met middellijn A1A2 heet hoofdcirkel van de ellips. De ingeschreven cirkel die gaat door het punt B, wordt in dit verband wel nevencirkel genoemd. [einde Opmerking]

In deze figuur:

• een cirkel met middelpunt O en straal a, die de x-as snijdt in de punten A₁ en A₂ en de y-as in het punt B₁;
• punt B is een willekeurig punt van de y-as; een cirkel met middelpunt O gaat door B;
• P is een willekeurig punt van de hoofdcirkel; door P gaat een halve lijn die de nevencirkel snijdt in het punt Q;
• de hoek van de halve lijn met de positieve x-as is f ;
• de lijn door Q loodrecht op de y-as snijdt de lijn door P loodrecht op de x-as in het punt X.

Wanneer nu P de hoofdcirkel doorloopt, doorloopt het punt X een ellips.

Klik hier voor een animatie bij deze constructie.

Bewijs:
Ook hier is natuurlijk een bewijs noodzakelijk.
Uitgaande van het punt P en de hoek f hebben we:
   waarbij .
Voor X geldt dan:
(3.1)…
Dit laatste kunnen we het snelst afleiden door het punt X (gelegen in een vlak W) op te vatten als orthogonale projectie van het punt P (gelegen in een vlak V), waarbij de hoek tussen V en W gelijk is aan t, met cos t = b/a, terwijl V en W elkaar snijden volgens de x-as (zie figuur 3b).

figuur 3b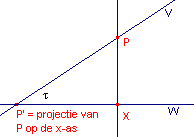

Nu is: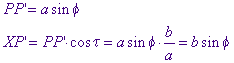

Uit het stelsel (3.1) volgt dan door kwadratering de vergelijking van de meetkundige plaats van het punt X:
   .

---

[ellips3.htm] laatste wijziging op: 22-12-2000