Ellips-constructies met Cabri [5]

Constructie  |  Bewijs   ][  Kegelsneden  |  Macro's voor kegelsneden  |  Cabri

5. Constructie gebaseerd op de verplaatsing van een lijnstuk (met vaste lengte) over twee snijdende lijnen

Johan de Witt (1625-1672), raadpensionaris van de Staten van Holland, voegt op 8 oktober 1658 aan een brief aan Frans van Schooten de Jongere (1615-1660) "eene aenspraecke aan UE" toe, waarin (in vertaling van Dr.A.W.Grootendorst) hij schrijft:

"Toen ik echter de leerboeken van de overige kromme lijnen -voorzover deze door de Ouden zijn overgeleverd en door jongeren zijn verklaard- nauwkeurig had bestudeerd, achtte ik het volslagen in te gaan tegen de natuurlijke orde -die men in de wiskunde zoveel mogelijk in acht moet nemen- dat men de oorsprong van deze krommen zoekt in een ruimtelijk lichaam en deze vervolgens overbrengt naar het platte vlak."

De Witt stoorde zich blijkbaar aan het feit, dat de bekende kegelsneden door de Grieken (onder wie Apollonius van Perga) de vlakke krommen via ruimtelijke beschouwingen genereerden, namelijk als doorsnijding van een kegel en een plat vlak.

In zijn boek "Elementa Curvarum Linearum" (Grondbeginselen van de Kromme Lijnen -voor het eerst uitgegeven in 1659 door Frans van Schooten de Jongere, als bijlage bij een vertaling van René Descartes' "La Géométrie") geeft Johan de Witt als eerste definities van de kegelsneden zonder daarbij gebruik te maken van een kegel (klik hier voor een samenvatting van de Elementa).

We geven de "definitie" van De Witt (opnieuw in vertaling van Dr.A.W. Grootendorst):

"Stel dat van een willekeurige rechthoekige driehoek één zijde - of deze nu de rechte hoek onderspant of tegenover één van de scherpe hoeken ligt - in deze hoek zodanig beweegt, dat elk eindpunt van deze bewegende zijde steeds ligt en blijft liggen op de zijde waarmee dit vanaf het begin verbonden was, terwijl deze zo nodig of naar de ene kant of naar de andere kant verlengd is.

Laat verder deze beweging voortgezet worden zowel over de nevenhoeken als over de overstaande hoek van de eerder genoemde hoek totdat de bewegende zijde is teruggekeerd in de beginstand.

Laat tenslotte door een willekeurig punt op deze lijn, of eventueel het verlengde daarvan, een kromme worden beschreven: […]"

Stelling Indien de eindpunten A en B van een lijnstuk met vaste lengte opvolgend op de benen l en m van een hoek liggen en op het lijnstuk (of het verlengde ervan) een punt X ligt, dan is de meetkundige plaats van de punten X een ellips, als de punten A en B de lijnen l en m doorlopen.

Opmerking

figuur 5a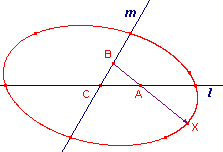

De Witt gaat uit van een rechthoekige driehoek. Maar ook met een willekeurige driehoek wordt een ellips gegenereerd.
[einde Opmerking]

We geven hieronder weer de Cabri-constructiestappen voor een rechthoekige driehoek ABC.
Zie figuur 5b.

figuur 5b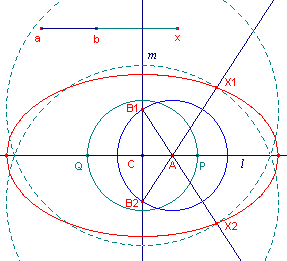

• Teken een lijnstuk ax (eindpunten aangegeven met kleine letters), met daarop een punt b. Teken ook het lijnstuk ab.
• Teken een punt C en daardoor twee loodrecht op elkaar staande lijnen l en m.
• Omdat het punt A (op l) maximaal de afstand ab kan afleggen ter weerszijden van C, construeren we op l een lijnstuk met C als midden ter lengte van 2ab:
• Teken de cirkel met middelpunt C en straal ab (met de functie "Passer"). Deze cirkel snijdt de lijn l in de punten P en Q.
• Teken het lijnstuk PQ en kies het punt A hierop.
• Op m zijn er nu twee punten, B₁ en B₂, op afstand ab van A.
  Teken de cirkel met middelpunt A en straal ab met de functie "Passer".
• Construeer op de halve lijnen B₁A en B₂A de punten X₁ en X₂ zodat B₁X₁ = ab en B₂X₂ = ab (met de functie "Passer").
• Als nu A het lijnstuk PQ doorloopt, dan bepalen X₁ en X₂ de ellips.

Klik hier voor een animatie bij deze constructie.

Bewijs:
We geven het bewijs op de moderne manier.

figuur 5c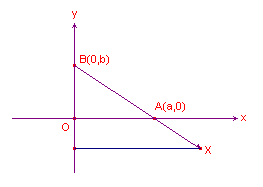

A(a,0) en B(0,b) zijn punten op opvolgend de x- en y-as. Stellen we de vaste lengte van AB gelijk aan p, dan is
(5.1) … a² + b² = p².
Zij X op (het verlengde van) AB zo gelegen, dat BX = kBA.
Voor de coördinaten van het punt X hebben we dan (zie figuur 5c):
   
Hieruit vinden we
   
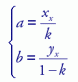
Substitueren we dit in de betrekking (5.1), dan krijgen we, met weglating van de index X:
   
Deling door p² geeft dan:
   
En dit is de vergelijking van een ellips.

---

[ellips5.htm] laatste wijziging op: 11-09-2010 (23-02-2000)