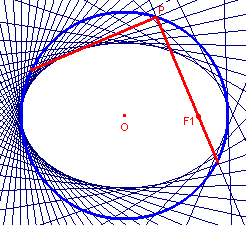
Over de richtcirkel van een ellips

Overzicht  ][  Richtlijn | Kegelsneden | Anal. meetkunde |  Meetkunde

Zie ook de pagina "Ellips-constructies [4b]".

0. Overzicht begin pagina

  1. Probleemstelling cabrisignal
  2. Constructies 1 en 2
       Constructie 1: een willekeurig punt
       Constructie 2: snijpunten met een lijn     cabrisignal
  3. De hoofdcirkel van een ellips cabrisignal
  4. Constructies 3, 4 en 5
       Constructie 3: brandpunten
       Constructie 4a: raaklijnen evenwijdig met een lijn     cabrisignal
       Constructie 5a: raaklijnen uit een punt     cabrisignal
  5. Constructies 4 en 5 in samenhang met de hoofdcirkel
       Constructie 4b: raaklijnen evenwijdig met een lijn
       Constructie 5b: raaklijnen uit een punt

1. Probleemstelling begin pagina

Probleem
Gegeven zijn een cirkel(F2, 2a) en een punt F1 binnen die cirkel.
Bepaal de meetkundige plaats van de middelpunten van de cirkels die (inwendig) raken aan cirkel(F2) en die door F1 gaan.

Oplossing: (zie figuur 1)

figuur 1 figuur 1 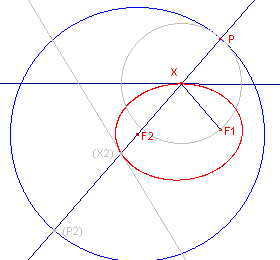Zij X een middelpunt van de gezochte cirkel. Omdat cirkel(X) raakt aan cirkel(F2) is XF2 een middellijn van die cirkel. Een snijpunt P (P2) daarvan met cirkel(F2) is het raakpunt.
Cirkel(X) gaat dan door F1 en P, zodat X op de middelloodlijn van PF1 ligt.
X kan dus gevonden worden als snijpunt van F2P en PF1, waarbij P willekeurig ligt op cirkel(F2).
Nu is XF2 + XF1 = XF2 + XP = F2P = 2a.
De meetkundige plaats is dus een ellips waarvan F1 en F2 de brandpunten zijn. De hoofdas van die ellips heeft de lengte 2a. ¨
.
Definitie
De cirkel(F2, 2a) heet richtcirkel van de ellips.

Opmerking
Als F1 buiten de cirkel(F2) ligt, is de meetkundige plaats een hyperbool.
Ligt F1 op de cirkel(F2), dan valt X samen met F2.
[einde Opmerking]

Klik hier Animatie voor een CabriJavapplet bij dit probleem.

Gevolgen
[1]
De ellips is volledig bepaald door de beide brandpunten en de richtcirkel (de lengte van de hoofdas ie gelijk aan de straal van de richtcirkel.
Zie ook de pagina "Ellips-constructies [4b]".
[2]
De middelloodlijn van PF1 is de raaklijn aan de ellips in het punt X.
Zie hiervoor ook de pagina "Twee raaklijnen aan een ellips", en wel paragraaf "Hoofdeigenschap van de raaklijn".
[einde Gevolgen]

2. Constructie 1 en 2 begin pagina
We gaan bij de constructies steeds uit van de in ligging gegeven brandpunten F1 en F2 van de ellips, en van de richtcirkel(F2, 2a), eventueel van de hoofdas A1A2.

[1] Construeer een willekeurig punt X van de ellips begin pagina

figuur 2 figuur 2 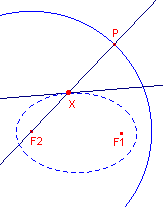(1) Kies het punt P op de richtcirkel.
(2) X is dan het snijpunt van de lijn F2P en de middelloodlijn van PF1.
¨

[2] Construeer de snijpunten van een lijn m met de ellips begin pagina

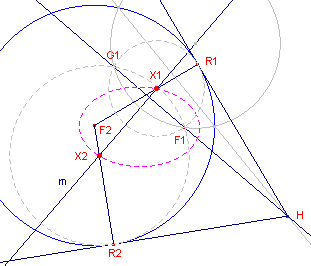figuur 3 richt3 De gezochte snijpunten zijn de op m gelegen middelpunten X1 en X2 van cirkels die gaan door F1 en die raken aan de richtcirkel(F2).
m is een middellijn van de gezochte cirkel (immers m gaat door X). Het spiegelbeeld G1 van F1 in m ligt dus ook op cirkel(X).
F1G1 is machtlijn van elk tweetal cirkels door F1 en G1. De beide gezochte cirkels hebben nu samen met cirkel(F2) een machtpunt H, dat op F1G1 ligt.
Het punt H is te construeren mbv. een willekeurige, cirkel(F2) snijdende, cirkel door F1 en G1, waarvan het middelpunt op m ligt.
De gezochte cirkels raken cirkel(F2), waaruit volgt, dat de machtlijn van cirkel(F2) en cirkel(X1) de gemeenschappelijke raaklijn is.

De raakpunten R1 en R2 kunnen nu eenvoudig gevonden worden met behulp van de raaklijnen uit H aan cirkel(F2).
X1 en X2 zijn dus de snijpunten van F2R1 en F2R2 en de lijn m.  ¨

Klik hier Animatie voor een CabriJavapplet bij deze constructie.

Gevolgen

figuur 4 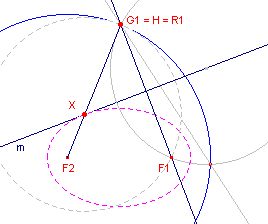richt4 [1]
(Zie figuur 4)
Als het punt G1 op de richtcirkel ligt, is er precies een oplossing. m is in dit geval dus raaklijn aan de ellips.
H valt nu samen met G1 (= R1).
Het middelpunt X (het raakpunt van m) is in dit geval het snijpunt van m en F2R1. ¨

[2]
Als het punt G1 buiten de richtcirkel ligt, zijn er geen snijpunten.
[einde Gevolgen]

3. De hoofdcirkel van een ellips begin pagina

Definitie
De hoofdcirkel van een ellips is de cirkel met de hoofdas van de ellips als middellijn.
.
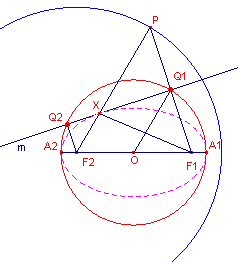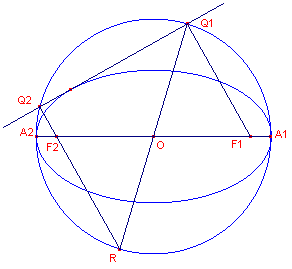
figuur 5 richt5 We bekijken nu een willekeurige raaklijn m aan de ellips, bepaald door het punt P op de richtcirkel.

Zij Q1 het voetpunt van de loodlijn uit F1 op m en O het midden van A1A2 (= 2a). O is dus ook midden van F1F2.
Dan is Q1O // PF2 en Q1O = ½PF2 = a.
Q1 ligt dus op de cirkel (O,a).
Zij Q2 het voetpunt van F2 op m.
De middelloodlijn van Q1Q2 (in het rechthoekig trapezium Q1Q2F2F1) gaat door O. Zodat OQ2 = OQ1 = a.
Q2 ligt dus eveneens op de cirkel(O,a). ¨

We hebben nu bewezen:

Stelling
De meetkundige plaats van de voetpunten van F1 en F2 op de raaklijnen aan een ellips is de hoofdcirkel van de ellips.

Klik hier Animatie voor een CabriJavapplet bij deze stelling.

Gevolgen

figuur 6 richt6
[1]
De ellips is op te vatten als de omhullende van een der benen van een rechthoek, waarvan het hoekpunt op een cirkel (de hoofdcirkel) ligt, terwijl het andere been door een vast punt (éen der brandpunten) gaat.

Klik hier Anmatie voor een CabriJavapplet bij figuur 6.
figuur 7 richt7 Het snijpunt R van F2Q2 en OQ1 ligt op de hoofdcirkel.
Uit de congruentie van de driehoeken OF1Q1 en OF2R volgt dan:
   F1Q1 = F2R
Nu is:
F1Q1 x F2Q2  =  F2R x F2Q2 = F2A2 x F2A1
= (a - c) (a + c)
= (a2 - c2)
= b2

Zodat:

[2]
Het product van de afstanden van de brandpunten tot een raaklijn is constant (gelijk aan het kwadraat van de halve nevenas van de ellips).

[einde Gevolgen]

4. Constructies 3, 4 en 5 begin pagina
We gaan bij deze constructies uit van de hoofdas A1A2, of ook weer van de richtcirkel.

[3] Constructie van de brandpunten als een punt P gegeven is begin pagina

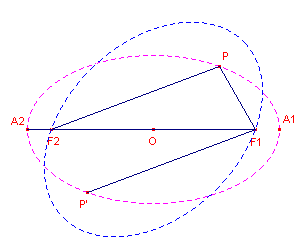figuur 8 richt8 Het spiegelbeeld P' van P in O (het midden vab A1A2) ligt ook op de ellips.Voor de gezochte punten F1 (en F2) geldt nu:
F1P + F1P' = PF1 + PF2 = 2a.
F1 ligt dus op een ellips met brandpunten P en P' en hoofdas met lengte 2a.
F1 en F2 zijn dus de snijpunten van A1A2 met deze tweede ellips.
Voor de uitvoering van de constructie zie verder Constructie 2. ¨

[4a] Constructie van de raaklijnen evenwijdig met een gegeven lijn als de brandpunten gegeven zijn begin pagina

figuur 9 figuur 9 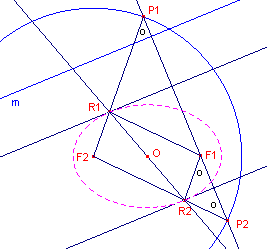Zij m de gegeven lijn.
Het spiegelbeeld P van F1 in een raaklijn (in de figuur zijn dit P1 en P2) ligt op de richtcirkel (zie Probleemstelling).
De loodlijn uit F1 op m snijdt dus de richtcirkel in de punten P1 en P2.
De middelloodlijnen van P1F1 en P2F2 zijn dus de gevraagde raaklijnen.
De snijpunten van P1F2 en P2F2 met deze lijnen zijn de raakpunten R1 en R2. ¨

 Klik hier Anmatie voor een CabriJavapplet bij deze constructie.
Gevolg
De lijn R1R2 (de verbindingslijn van de raakpunten van twee evenwijdige raaklijnen) is middellijn van de ellips.

Bewijs: (zie figuur 9)
hF2P1P2 = hF1R2P2 = hR2F1F2. Dus F1R2 // R1F2.
Analoog ook F1R1 // F2R2, zodat F1R1F2R2 een parallellogram is.
R1R2 is daarin diagonaal. Dus gaat R1R2 door het midden O van F1F2.  ¨
[einde Gevolg]

[5a] Constructie van de raaklijnen uit een punt P als de brandpunten gegeven zijn begin pagina

figuur 10 figuur 10 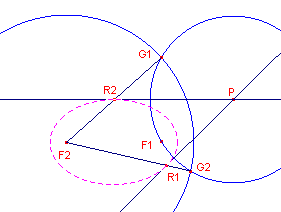De beelden G1 en G2 van F1 in de raaklijnen door P liggen op de richtcirkel. Hierdoor is PG1 = PG2.
De punten G1 en G2 liggen dan op een cirkel(P,PF1) met behulp waarvan de punten G1 en G2 kunnen worden geconstrueerd.
De raaklijnen zijn dan de middelloodlijnen van de lijnstukken F1G1 en F2G2.
De raakpunten R1 en R2 zijn de snijpunten van de stralen F2G1 en F2G2 en die lijnen). ¨

Klik hier Anmatie voor een CabriJavapplet bij deze constructie.

5. Constructies 4 en 5 in samenhang met de hoofdcirkel begin pagina

[4b] Constructie van de raaklijnen evenwijdig met een gegeven lijn als de brandpunten gegeven zijn begin pagina

figuur 11 figuur 11 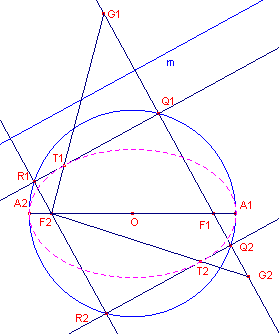Zij m de gegeven lijn.
De voetpunten Q1 en Q2 van de loodlijnen uit F1 en F2 op de raaklijnen liggen op de hoofdcirkel.
Q1 en Q2 zijn ds de snijpunten van de loodlijn uit F1 op de lijn m (en R1 en R2 uit F2).
De raakpunten kunnen worden gevonden via de speigelbeelden G1 en G2 in de raaklijnen: F2G1 en F2G2 snijden de raaklijnen in de bijbehorende raakpunten T1 en T2. ¨

[5b] Constructie van de raaklijnen uit een punt P als de brandpunten gegeven zijn begin pagina

figuur 12 figuur 12 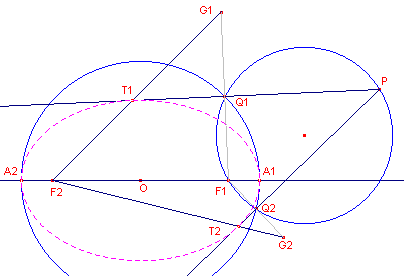De voetpunten Q1 en Q2 van de loodlijnen uit F1 op de raaklijnen worden gevonden als snijpunten van de hoofdcirkel en de cirkel met PF1 als middellijn.
De raaklijnen zijn dus de lijnen PQ1 en PQ2.
De raakpunten T1 en T2 worden gevonden met behulp van de spiegelbeelden G1 en G2 van F1 in de raaklijnen. ¨

begin pagina

[richtcirkel.htm] Laatste wijizging op: 02-01-01