Prisma

Overzicht  ][  Overzicht stereo | Axioma's | Cabri 3D

Overzicht terug

  1. Definitie, basiseigenschappen
  2. Loodrechte doorsnede
  3. Soorten prisma's
  4. Doorsnede
  5. Driezijdig prisma en viervlak

1. Definitie, basiseigenschappen terug

Definitie
Een prisma is een lichaam (veelvlak) dat begrensd wordt door enige vlakken die elkaar volgens evenwijdige lijnen snijden en door twee evenwijdige vlakken
of
Een prisma is een veelvlak waarvan twee zijvlakken in evenwijdige vlakken liggen en de overige zijvlakken evenwijdig zijn met eenzelfde lijn die de evenwijdige vlakken snijdt.
.
figuur 1
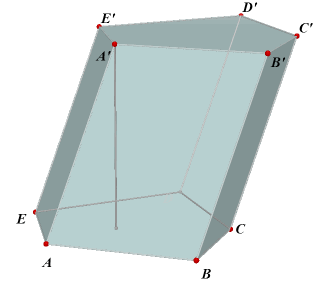prisma1 In de figuur hiernaast zien we een vijfzijdig prisma.
De evenwijdige vlakken (uit de definitie) worden grondvlak en bovenvlak genoemd: ABCDE en A'B'C'D'E'.
De (opstaande) zijvlakken zijn ABB'C, BCC'B', CDD'C", DEE'D", EAA"E.
De snijlijnen van de zijvlakken zijn de ribben van het viervlak.
De afstand tussen het grond- en bovenvlak is hoogte van het prisma.

Klik hier >Cabri 3D applet< voor een Cabri 3D applet van figuur 1 (automatisch draaiend; opent in een NieuwVenster)

Nb.
Het aantal zijvlakken bepaalt dus het soort viervlak: driezijdig, vierzijdig, ...
.
Stelling 1
(1) De zijvlakken van een prisma zijn parallellogrammen.
(2) Grond- en bovenvlak van een prisma zijn congruente veelhoeken.

Bewijs:
(1) Het grondvlak en het bovenvlak zijn evenwijdig. Beide vlakken worden gesneden door vlak ABB'A', zodat AB // A'B" ...... (i)
Per definitie is AA' // BB' ...... (ii)
Uit (i) en (ii) volgt dat ABB'A' een parallellogram is. Evenzo voor de andere zijvlakken.¨

(2) Uit (1) volgt dat de zijden van grond- en bovenvlak gelijk zijn. Omdat de zijden van grond- en bovenvlak evenwijdig zijn, zijn ook de benen van de hoeken in het grondvlak evenwijdig met de benen van de hoeken in het bovenvlak. Deze hoeken zijn dus twee aan twee gelijk. Dan zijn grond- en bovenvlak congruent.¨

2. Loodrechte doorsnede terug

Definitie
Een loodrechte doorsnede van een prisma is een vlak dat loodrecht staat op de opstaande ribben en alle opstaande ribben snijdt.
.
figuur 2
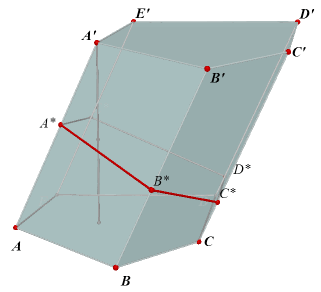prisma2 In de figuur hiernaast is A*B*C*D*E* een loodrechte doorsnede van het prisma ABCDE.A'B'C'D'E'.

Opmerking
Is ook A"B"C"D"E" een loodrechte doorsnede, dan is A*B*C*D*E*.A"B"C"D"E een recht prisma.
Uit stelling 1.2 volgt dan dat grondvlak en bovenvlak van dat prisma congruent zijn.
Twee loodrechte doorsnedes van een prisma zijn dus congruent.
[einde Opmerking]
.
Stelling 2
De zijdelingse oppervlakte van een prisma is gelijk aan het product van de omtrek van de loodrechte doorsnede met één der opstaande ribben.

Bewijs:
In figuur 2 is A*B* de hoogte van het parallellogram ABB'A". Opp(ABB'A") = A*B* · AA'. En ook: Opp(BCC'B') = B*C* · BB', ...
Met AA' = BB' = ... geeft dit:
Zijdelingse oppervlakte prisma = AA' · (A*B* + B*C* + ...)
Waarmee het gestelde is aangetoond.¨

Opmerking
Zie ook de pagian "Van scheef prisma naar recht prisma" voor de betekenis van de loodrechte doorsnede voor de inhoud.
[einde Opmerking]

3. Soorten prisma's terug

Recht prisma: prisma waarvan de ribben loodrecht staan op het grondvlak.
Regelmatig prisma: een recht prisma waarvan het grondvlak (en bovenvlak) regelmatige veelhoeken zijn.
Parallellepipedum of blok (*): (vierzijdig) prisma waarvan het grondvlak een parallellogram is.
Recht blok: parallellepipedum waarvan de ribben loodrecht staan op het grondvlak.
Rechthoekig blok of (gewoon) balk: recht blok waarvan het grondvlak een rechthoek is (zijvlakken en grond- en bovenvlak zijn rechthoeken).
Ruitenzesvlak: een prisma warvan het grondvlak een ruit si en de zijvlakken eveneens; zie ook de pagina "Ruitenzesvlak".
Kubus: rechthoekig blok waarvan de zijvlakken een vierkant zijn (zijvlakken en grond- en bovenvlak zijn vierkanten); zie ook de pagina Kubus.

(*) De term blok is afkomstig van Simon Stevin (1548-1620, Vlaanderen).

Overige definities:   Zijvlaksdiagonaal: een lijnstuk, niet zijnde een ribbe, dat twee hoekpunten gelegen in hetzelfde vlak met elkaar verbindt.
Lichaamsdiagonaal: een lijnstuk, niet zijnde een ribbe of een zijvlaksdiagonaal, dat twee hoekpunten met elkaar verbindt.
Zijdelingse oppervlakte: de som van de oppervlaktes van de zijvlakken.
.
Stelling 3
De lichaamsdiagonalen van een blok snijden elkaar in hetzelfde punt.

Bewijs:

figuur 3
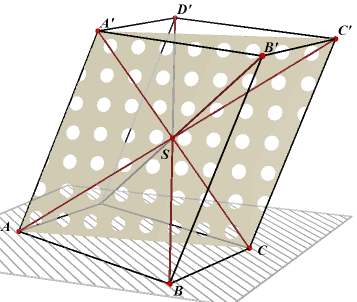prisma3
A'C' // AC. Deze lijnen liggen dus in een vlak (ACC'A'). Ze snijden elkaar in het punt S, waarbij S het midden is van AC'.
Zo ook AC' en D'B. D'B snijdt AC' eveneens in het punt S, en dat geldt analoog voor DB'.
AC' wordt dus door elke anderew lichaamsdiagonaal middendoor gedeeld.
Waarmee het gestelde is aangetoond.¨
.
Stelling 4
De lichaamsdiagonalen van een rechthoekig blok (balk) zijn gelijk.

Bewijs:

figuur 4
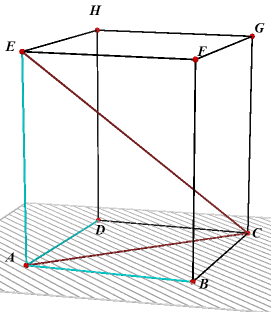
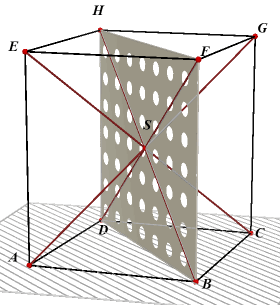prisma4 BFHD is nu een rechthoek. De lijnstukken BH en DF zijn dus gelijk.
En dat geldt ook voor BH en CE en voor BH en AG.
Waarmee de stelling bewezen is.¨
.
Stelling 5
Het kwadraat van een lichaamsdiagonaal van een rechthoekig blok (balk) is gelijk aan de som van de kwadraten van de drie in hetzelfde hoekpunt samenkomende ribben.

Bewijs:

figuur 5a

prisma3b

 In rechthoek ABCD is AC2 = AB2 + BC2 = AB2 + AD2.
In rechthoek ACGE is CE2 = AC2 + AE2, zodat
CE2 = AB2 + AD2 + AE2
Waarmee, samen met het gegeven in stelling 4,  het gestelde is aangetoond.
Gevolg
Voor de hoeken x, y, z die een lijn p maakt met drie loodrecht op elkaar staande lijnen l, m, n geldt
cos2 x + cos2 y + cos2 z  =1

Bewijs:
figuur 5b
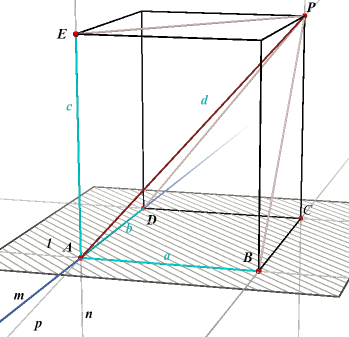prisma5 We nemen aan dat de lijnen l, m, n door een punt A gaan.
Is dat niet het geval, dan kunnen er aan die lijnen evenwijdige lijnen door het punt A worden beschouwd.
We veronderstellen eveneens dat de lijn p door A gaat.
Op de lijnen l, m, n, met punt A als hoekpunt en een wilelkerig punt P van p kan een balk worden geconstrueerd (zie figuur hiernaast), met in A samenkomende ribben met lengtes a, b, c en AP = d.
Nu is (in ABP) cos x = a / d, (in ADP) cos y = b / d, (in AEP) cos z = c / d.
Volgens stelling 5 is dan:
   a2 + b2 + c2 = d2
zodat inderdaad
   cos2 x + cos2 y + cos2 z  = 1
¨

4. Doorsnede terug
Constructie van de doorsnede van een in tekening gegeven prisma met een vlak.
Nb. Vlakken kunnen op verschillende manieren worden vastgelegd. We behandelen hieronder slechts een van deze manieren.

figuur 6
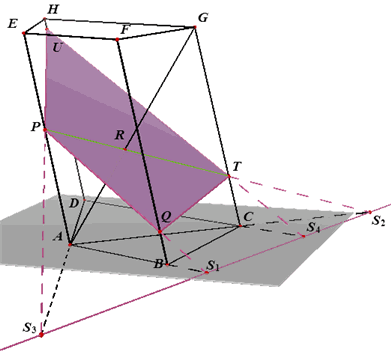prisma6 Gegeven:
Prisma ABCD.EFGH.
Vlak V = PQR wordt geven door:
P op ribbe AE, Q op BF, R op lichaamsdiagonaal AG.

Gevraagd:
De doorsnede van V met het prisma.

Constructiebeschrijving:
PQ ligt in ABEF. PQ snijdt AB in het punt S1.
PR ligt in vlak ACGE (een digonaalvlak).
PR snijdt AC in S2 en PR snijdt CG in T.
De lijn S1S2 is dus de snijlijn van V met het grondvlak ABCD; deze snijlijn wordt ook wel collineatie-as genoemd.
V snijdt AD in S3 = S1S2 /\ AD.
De lijn S3P ligt in vlak ADHE en snijdt DH in het punt U.
Vierhoek PQTU is de doorsnede van V met het prisma.¨

5. Driezijdig prisma en viervlak terug

Stelling 6
Een driezijdig prisma kan worden verdeeld in drie viervlakken die dezelfde inhoud hebben.

Bewijs:

figuur 7
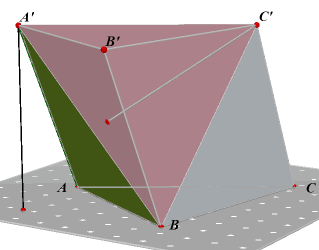prisma7 We hebben de viervlakken A'.ABC en C'.ABC.
Deze viervlakken hebben hetzelfde grondvlak (namelijk ABC) en dezelfde hoogte (nl. de loodlijn uit A op het vlak ABC).
De viervlakken C'.ABA' (congruent met A'.ABC) en C'.A'BB' hebben congruente grondvlakken en dezelfde hoogte (nl. de loodlijn uit C' op vlak ABB'A').
Uitgaande van de stelling dat viervlakken met gelijk grondvlak en gelijke hoogte een even grote inhoud hebben. komt men tot de formule voor de inhoud van een viervlak:

     I viervlak = G . h / 3

waarbij G de oppervlakte is van het grondvlak en h de hoogte van het viervlak.¨

Klik hier >cabri3dsmall< voor een Cabri3D applet bij figuur 7 (opent in een NieuwVenter; automatisch draaiend).

Opmerking
Bij het bewijs van stelling 6 is impliciet verondersteld dat de inhoud van een driezijdig prisma gelijk is aan G . h, waarbij G de oppervlakte is van het grondvlak (of van het bovenvlak) en h de afstand tussen grondvlak en bovenvlak.
Zie ook de pagina "Inhoud van viervlak en piramide" en de pagina "Van scheef prisma via recht prisma naar blok".
[einde Opmerking]

begin pagina
[p : prisma.htm] laatste wijziging op: 26-09-2005