Van schreef prisma via recht prisma naar blok

[ Overzicht stereo | Cabri 3D ]

Stelling 1
De inhoud van een scheef prisma met loodrechte doorsnede D en opstaande ribbe a is gelijk aan de inhoud van een recht prisma met grondvlak D en opstaande ribbe a.

Bewijs:

figuur 1

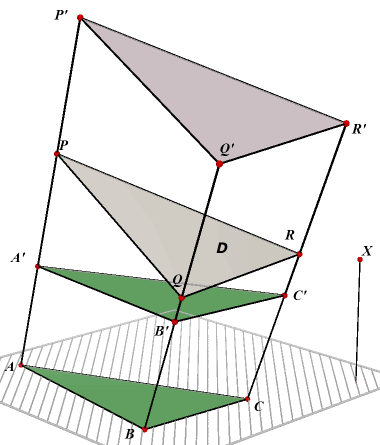In nevenstaande figuur is A'B'C'.ABC het scheve prisma met ribbe a (a = AA'); P'Q'R'.PQR is het rechte prisma, waarvan PQR de loodrechte doorsnede is van het scheve prisma (PP' = a; Opp(PQR) = D).

We kunnen het rechte prisma zo plaatsen, dat de ribben ervan liggen op de dragers van de ribben van het scheve prisma.
De plaatsing is zodanig, dat het afgeknotte prisma A'B'C'.PQR een inhoud I' heeft.
Zij nu I_s de inhoud van het scheve prisma en I_r de inhoud van het rechte prisma. We moeten nu bewijzen dat I_s = I_r.

We bekijken de translatie over de vector A'A.
Hierdoor gaat P'Q'R' over in PQR, en A'B'C' in ABC, immers PP' = AA' = QQ' = BB' = RR' = CC
Hierdoor neemt het risma P'Q'R'.A'B'C' de plaats in van het prisma PQR.ABC.'
En dan is: I_r + I' = I_s + I', zodat inderdaad
I_r = I_s
Waarmee stelling 1 is bewezen.¨

Klik hier >< voor een Cabri 3D applet die het bovenstaande bewijs illustreert.

Nb.
In het bovenstaande bewijs wordt niet gesproken over de vorm van het grondvlak van het prisma. Dat kan in principe elke veelhoek zijn. Het bewijs ondervindt daardoor danook geen verandering bij vierzijdige, vijfzijdige, ... prisma's.

Voor de (daadwerkelijke) berekening van de inhoud van prisma's (als functie van de lengtes van de ribben) gaan we uit van de volgende definitie:

Definitie
De inhoud I van een rechthoekig blok (balk) is gelijk aan het product van lengte, breedte en hoogte (I = l.b.h).
l, b en h zijn de lengtes van de ribben die in één hoekpunt van de balk samenkomen.

Opmerking. Is G = l . b dan is dus I = Gh.

Een direct gevolg van stelling 1 is:

Stelling 2
De inhoud van een recht blok is gelijk aan het product van grondvlak en hoogte.

Bewijs:

figuur 2

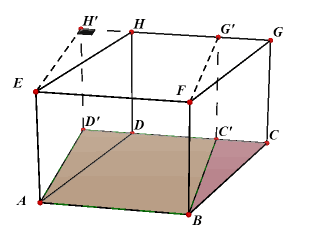EFGH.ABCD is een recht blok.

BC'G'F is een loodrechte doorsnede daarvan.
De blokken EFG'H'.ABC'D' en EFGH.ABCD hebben volgens stelling 1 dezelfde inhoud.
EFG'H'.ABC'D' is echter een rechthoekig blok. Volgens de definitie is de inhoud daarvan gelijk aan grondvlak maal hoogte.
De oppervlakte van ABCD gelijk is aan die van ABC'D' en beide blokken hebben ook dezelfde hoogte hebben, waarmee de stelling bewezen is.¨

En uit stelling 2 vinden we dan direct:

Stelling 3
De inhoud van een scheef blok is gelijk aan het product van grondvlak en hoogte.

Bewijs:

figuur 3

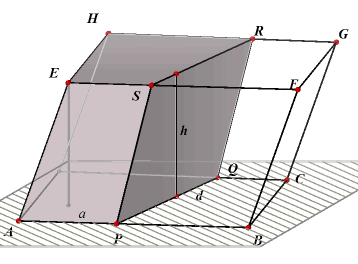PQRS is de loodrechte doorsnede van het scheve blok ABCD.EFGH, waarvan de ribbe AB gelijk is aan a.
Volgens stelling 1 is nu de inhoud vasn dat blok gelijk aan Opp(PQRS) maal a.
Zij nu verder PQ = SR = d en bedenken we verder dat de afstand van PQ en SR gelijk is aan h (tevens de hoogte van het blok), dan is Opp(PQRS) = d h.
De inhoud I van het blok is dan:
I = a d h = ad . h = Opp(ABCD) . h = grondvlak maal hoogte.¨

Samenvattend:

Stelling 4
De inhoud van elk blok is gelijk aan het product van grondvlak en hoogte.

En vervolgens:

Stelling 5
Een blok wordt door een diagonaalvlak verdeeld in twee (driezijdige) prisma's met gelijke inhoud.

Bewijs:

figuur 4

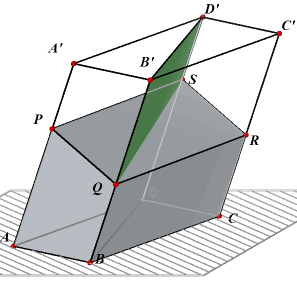In de figuur hiernaast zien we het blok ABCD.A'B'C'D'.
PQRS is een loodrechte doorsnede daarvan.
BDD'B is een diagonaalvlak van het prisma.
We moeten nu bewijzen dat de prisma's ABD.A'B'D en BCD.B'C'D' dezelfde inhoud hebben.

PQRS is een parallellogrma. QS is een diagonaal daarvan. Dus de driehoeken PQS en QRS zijn congruent.
PQS en QRS zijn tevens loodrechte doorsnede van de beide driezijdige prisma's.
Beide prisma's hebben dezelfde opstaande ribbe.
Volgens stelling 1 zijn de inhouden van beide driezijdige prisma's aan elkaar gelijk.¨

We kunnen nu eenvoudig bewijzen:

Stelling 6
De inhoud van een driezijdig prisma is gelijk aan het product van de loodrechte doorsnede en de opstaande ribbe, en tevens gelijk aan het product van grondvlak en hoogte.

Bewijs:
Het eerste deel van het bewijs vinden we terug in het bewijs van stelling 5.
In figuur 4 is de inhoud van blok ABCD.EFGH gelijk aan Gh (volgens stelling 4).
De grondvlakken van beide driezijdige deelprisma's zijn congruent (beide dus gelijk aan G' = ½G. De deelprisma's hebben beide dezelfde hoogte (gelijk aan die van het gehele prisma).
En daaruit volgt dan het tweede deel van hetgeen moest worden bewezen.¨

Opmerking. Zie voor stelling 6 ook de pagina "Inhoud", stelling 3.

Gevolg
Elk n-zijdig prisma (met n > 3) kan worden verdeeld in n - 2 driezijdige prisma's.
En stelling 6 kan dan op die deelprisma's worden toegepast.
We vinden eenvoudig:

Stelling 7
De inhoud van een prisma is gelijk aan het product van de loodrechte doorsnede en een opstaande ribbe, en ook gelijk aan het product van het grondvlak en de hoogte.

[p : prismasr.htm] laatste wijziging op: 26-09-2005