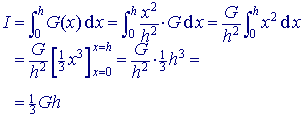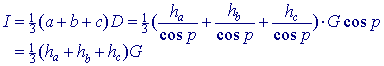Inhoud van viervlak en piramide (en meer)

Overzicht ][ Overzicht stereo | Cabri 3D

Zie ook de pagina "Nog meer over de inhoud van een viervlak".

Overzicht

Inhoud viervlak en piramide

En meer....

Inhoud afgeknotte piramide
Inhoud scheef prisma
Inhoud afgeknot prisma
Inhoud afgeknot prisma, een tweede bewijs

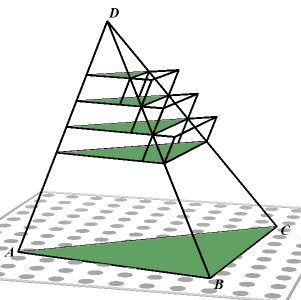
1. Inhoud viervlak en piramide

figuur 1

De inhoud van een piramide (en van een viervlak, opgevat als driezijdige piramide) kan worden bepaald door de piramide in een groot aantal 'schijven' te verdelen (die schijven zijn dan afgeknotte piramides) en die schijven dan te voorzien van ingeschreven en omgeschreven prisma's.
De schijven zijn evenwijdig met het grondvlak (zie de figuur hiernaast).
De inhoud van de piramide kan dan worden bepaald via limietbeschouwingen van de som van de inhouden van die in- en omgeschreven prisma's (ondersom en bovensom).

We kunnen de inhoudsbepaling ook (direct) laten berusten op de integraalrekening.

Stelling 1
Voor de inhoud I van een piramide T.ABC... geldt: I = 1/3 Gh

Bewijs:
Door de top T van de piramide brengen we een assenstelsel aan waarvan de x-as valt langs de hoogtelijn door T op het grondvlak.
Is de oppervlakte van het grondvlak gelijk aan G, dan zal de oppervlakte van een doorsnede evenwijdig met het grondvlak een functie zijn van de afstand x van T tot die doorsnede.

figuur 2

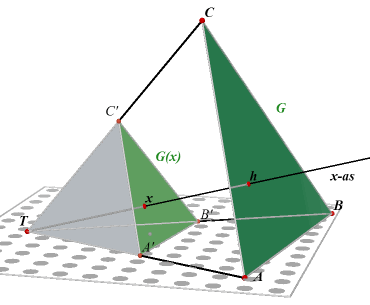Is de oppervlakte van zo'n doorsnede G(x) en h de hoogte van de piramide, dan is

G(x) = (x² / h²) . G

Nu geldt:

inhoudf1

De inhoud van piramide (cq. viervlak) is dus gelijk aan ¹/₃ van het product van het grondvlak en de hoogte:
I = ¹/₃Gh

Nb. In de berekening hierboven kunnen G(x) en dx worden beschouwd als resp. grondvlak en hoogte van de prismavormige schijven.

Opmerking. Zie ook de pagina "Prisma" (stelling 6).

2. Inhoud afgeknotte piramide

Definitie
Een afgeknotte piramide is een veelvlak (niet zijnde een piramide) dat ontstaat door de opstaande ribben van een piramide te snijden met een vlak dat evenwijdig is met het grondvlak.

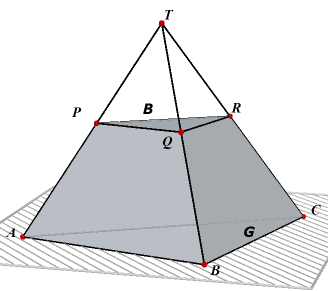
figuur 3a		figuur 3b

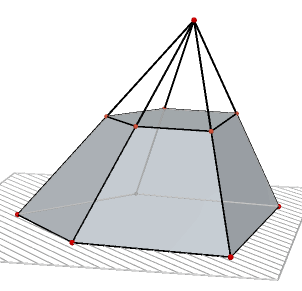afgeknot viervlak		afgeknotte vijfzijdige piramide

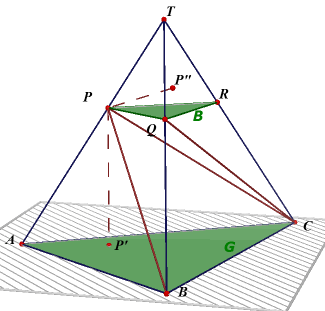
Stelling 2
Voor de inhoud I van de afgeknotte piramide PQR.ABC (zie figuur 3a) geldt: I = ¹/₃h(B + G + Ö(BG) ).
Hierin stellen B en G de oppervlaktes van resp boven- en ondervlak voor van de afgeknotte piramide; h is de hoogte ervan (de afstand tussen de vlakken PQR en ABC).

Bewijs:

figuur 4

De afgeknotte piramide is opgebouwd uit de viervlakken:
P.ABC, P. BCQ en C.PQR.
De hoogte PP' van P.ABC is gelijk aan h (de hoogte van de afgeknotte piramide).
De hoogte van C.PQR is eveneens gelijk aan h.
De hoogte van P.BCQ is de afstand PP" van P tot het vlak BCT.
Voor P.ABC hebben we dus: Inh(P.ABC) = ¹/₃ . Gh ......(i)
Voor C.PQR hebben we Inh(C.PQR) = ¹/₃ . Bh ......(ii)

We kunnen C.PQR ook opvatten als P.QCR, zodat
Inh(P.BCQ) = ¹/₃ . PP" . Opp(BCQ)
Inh(P.CQR) = ¹/₃ . PP" . Opp(CQR)
Opp(BCQ) en Opp(CQR) verhouden zich (vanwege de evenwijdige 'bases' BC en QR) als:
BC : QR.
Maar BC : QR = Ö(G) : Ö(B)

Dus Inh(P.BCQ) = Ö(G) / Ö(B) . Inh(P.CQR) = Ö(G) / Ö(B) .¹/₃ . Bh

Zodat Inh(P.BCQ) = ¹/₃h . Ö(GB) ......(iii)
Uit (i), (ii) en (iii) volgt nu:
I = Inh(PQR.ABC) = ¹/₃h(G + B + Ö(GB) )
Waarmee het gestelde is aangetoond.¨

Opmerking
Aan de structuur van de formule voor de inhoud I is te zien, dat deze ook geldt voor afgeknotte piramides met meer dan drie zijvlakken.
[einde Opmerking]

3. Inhoud scheef prisma

Stelling 3
De inhoud van een scheef prisma is gelijk aan de oppervlakte van een loodrechte doorsnede vermenigvuldigd met de lengte van een opstaande ribbe.

Bewijs:

figuur 5a
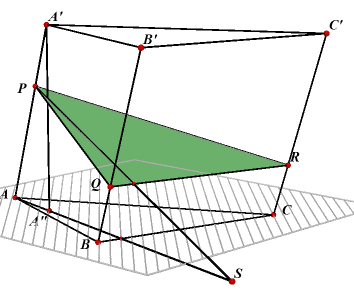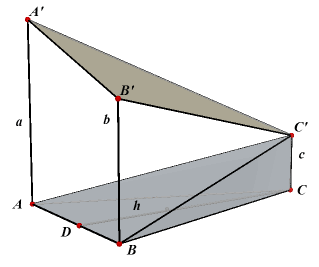
	In nevenstaande figuur is PQR een loodrechte doorsnede van het scheve prisma A'B'C'.ABC. A" is de projectie van A' op het grondvlak. De hoek PSA is de hoek tussen de vlakken PQR en ABC (standhoek). Stel PSA = a, dan is ook AA'A" = a. Dus cos(a) = A'A" / AA' (in driehoek AA'A"). Daardoor is Inh(A'B'C'.ABC) = Opp(ABC) . A'A" = Opp(ABC).AA'.cos(a) ......(i) Wegens de projectie van PQR op ABC is dan ook Opp(ABC) .cos(a) = Opp(PQR). Zodat uit (i) volgt: Inh(A'B'C'.ABC) = Opp(PQR) . AA' Waarmee de stelling bewezen is.¨
figuur 5b
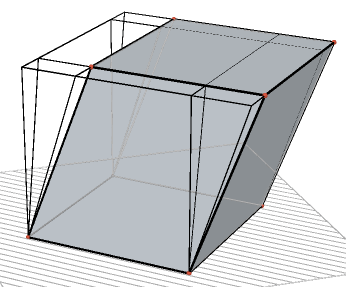	Opmerking Door afsnijding en aanvulling van congruente veelvlakken is het mogelijk een (scheef) prisma te veranderen in een rechthoekig blok. Daarmee wordt aannemelijk dat voor de inhoud I van een prisma geldt I = Gh waarbij G de oppervlakte is van het grondvlak en h de afstand tussen grnd- en bovenvlak (de hoogte). Hiernaast is een dergelijke 'constructie' weergegeven. Zie verder ook de pagina "Van scheef prisma via recht prisma naar blok". [einde Opmerking]

4. Inhoud afgeknot prisma

Stelling 4
De inhoud van een afgeknot prisma is gelijk aan de oppervlakte van een loodrechte doorsnede vermenigvuldigd met het gemiddelde van de lengtes van de opstaande ribben.

Nb.
In tegenstelling tot een afgeknotte piramide, waarbij de afknotting plaats vindt door een vlak evenwijdig met het grondvlak, wordt de afknotting van een prisma gerealiseerd met een vlak dat niet evenwijdig is met het grondvlak.

Bewijs:
We bewijzen de stelling voor een afgeknot driezijdig prisma (afgeknot viervlak).

figuur 6a
	(a) We bekijken allereerst een recht afgeknot prisma, waarvan de opstaande ribben loodrecht op het grondvlak ABC staan. Het prisma bestaat allereerst de piramide C'.ABC waarvan de inhoud gelijk is aan Inh(C'.ABC) = ¹/₃G.c waarbij G = Opp(ABC) en c de lengte van CC'. En vervolgens is het andere deel de piramide C'.AA'B'B. Hiervan is de inhoud gelijk aan Inh(AA'B'B) = ¹/₃.h.Opp(AA"BB') waarbij h de afstand is van C tot AA'B'B. Omdat het prisma een recht prisma is, ligt h in het vlak ABC; met andere woorden: h is de loodlijn uit C op AB (h = CD). Nu is AA'B'B een rechthoekig trapezium met evenwijdige zijden a en b en hoogte AB. We vinden dan: Inh(C'.AA'B'B) = ¹/₃. h . ¹/₂ (a + b) . AB waarbij ¹/₂ . h . AB = G = Opp(ABC). Dus Inh(C'.AA'B'B) = ¹/₃ . (a + b) . G, zodat Inh(A'B'C'.ABC) = ¹/₃(a+b+c) . G
figuur 6b
	(b) In figuur 6b is PQR een vlak dat loodrecht staat op de ribbe AD (en dus ook loodrecht op de andere twee opstaande ribben). Een afgeknot prisma is (daardoor) te beschouwen als de 'som' van twee afgeknotte rechte prisma's. Hiernaast zijn dat: PQR.A'B'C' en PQR.ABC. Volgens het bovenstaande bij (a) is dan de inhoud van ABC.A'B'C': Inh(ABC.A'B'C') = ¹/₃(a₁ + b₁ + c₁) D + ¹/₃(a₂ + b₂ + c₂) D = ¹/₃(a + b + c) D Waarmee het gestelde is aangetoond.¨

Opmerking
Zij p de hoek tussen de vlakken PQR en ABC, dan is D = G cos(p). We zullen dit resultaat gebruiken in paragraaf 5, bij stelling 5.
[einde Opmerking]

5. Inhoud afgeknot prisma, een tweede bewijs

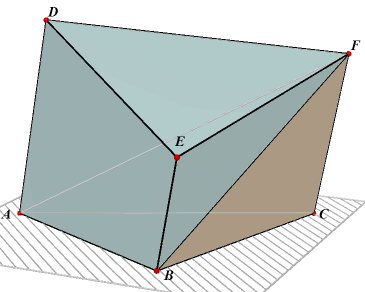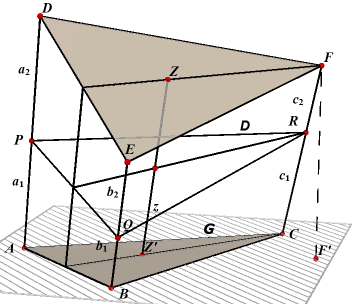
We bekijken opnieuw het afgeknotte prisma DEF.ABC.

We kunnen dit afgeknot prisma opgebouwd denken uit het viervlak F.ABC en de piramide F.ABED, zodat
Inh(DEF.ABC) = Inh(F.ABC) + Inh(F.ABDE)/
Elk punt van het lijnstuk CF heeft gelijke afstand tot vlak ABED, immers CF // ABED.
De inhoud van F.ABDE kan dus vervangen worden door elke andere piramide met grondvlak ABED, als de top ervan maar op CF ligt.

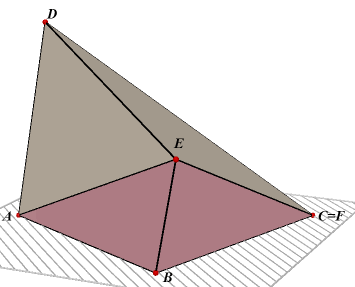We kiezen danook het punt C als top van die 'vervangende' piramide. Dus:
Inh(F.ABED) = Inh(C.ABED)
De piramide C.ABDE kan op diens beurt weer opgebouwd worden met het viervlak E.ABC en het viervlak E.ADC, zodat
Inh(F.ABED) = Inh(E.ABC) + Inh(A.ADC)
Elk punt van het lijnstuk BE heeft gelijke afstand tot vlak ADC, immers BE // ADC.
De inhoud van A.ADC kan dus vervangen worden door elk andere viervlak met grondvlak ADE, mits de top maar op BE ligt.

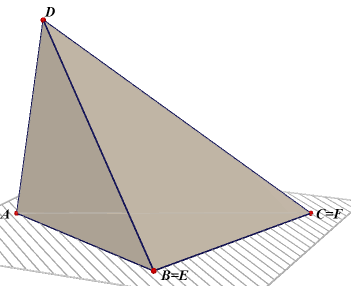We kiezen nu B als top van het 'vervangende' viervlak. Dus:
Inh(E.ADC) = Inh(B.ADC) = Inh(D.ABC)
immers voor die viervlakken geldt B.ADC = D. ABC

Voor het afgeknotte prisma DEF.ABC hebben we dus gevonden:

Inh(DEF.ABC) = inh(F.ABC) + Inh(E.ABC) + Inh(D.ABC)

Of geformuleerd als stelling:

Stelling 5
De inhoud van een afgeknot driezijdig prisma is gelijk aan de som van de inhouden van de viervlakken met het grondvlak van het prisma als grondvlak en de hoekpunten van het bovenvlak als top.

Nb.
Eenzelfde redenering kan worden opgezet voor vierzijdige, vijfzijdige, ... afgeknotte prisma's.

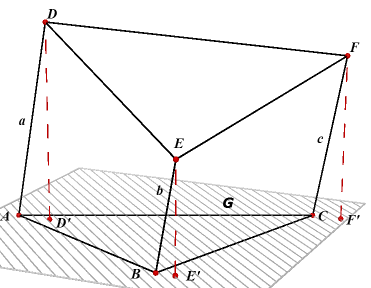Gevolg van stelling 5
Zijn DD' = h_a, EE' = h_b en FF' = h_c de afstanden van D, E, F tot het grondvlak ABC, met oppervlakte G, dan geldt:

Inh(DEF.ABC) = ¹/₃ (h_a +h_b + h_c) G

Dit resultaat kunnen we ook vinden via de volgende redenering.
Zij p de hoek tussen een loodrechte doorsnede (oppervlakte gelijk aan D) van het afgeknotte prisma en het vlak ABC. Dan is
h_a = a cos(p), h_b = b cos(p) en h_c = c cos(p), met D = G cos(p) - zie de opmerking aan het eind van paragraaf 4 - zodat
inhoudf2

[p : inhoud.htm] laatste wijziging op: 25-03-2009 (01-10-2005)