Nog meer over de inhoud van een viervlak

Overzicht ][ Inhoud van viervlak en priamide (en meer) | Overzicht stereo | Cabri 3D

Overzicht

Stelling 1: Inhoud van twee viervlakken met een gemeenschappelijke drievlakshoek
Stelling 2: Inhoudsverdeling via een vlak door de middens van twee overstaande ribben

Stelling 1

De inhouden van twee viervlakken die een drievlakshoek gemeenschappelijk hebben, verhouden zich als de producten van de ribben van het viervlak die gelegen zijn op de ribben van die drievlakshoek.

Bewijs:

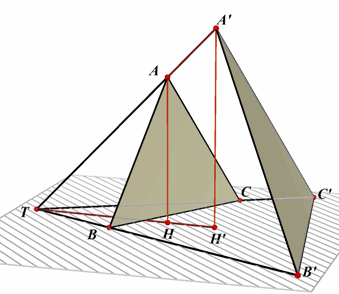Zonder de algemeenheid geweld aan te doen denken we de beide viervl;akken TABCD en TA'B'C' geplaatst als in de figuur hiernaast.
We projecteren A en A' op het vlak TB'C'.
Nu is (met a = hoek BTC)

Inh(TABCD) : Inh(TA'B'C')	=	Inh(A.TBC) : Inh(A'.TB'C')
	=	¹/₃AH · Opp(TBC) : ¹/₃A'H' · Opp(TB'C')
	=	AH · TB · TC · sin(a) : A'H' · TB' · TC' · sin(a)
	=	(AH · TB · TC) : (A'H' · TB' · TC')

Maar: AH : A'H' = TA : TA', dus:

:Inh(TABCD) : Inh(TA'B'C") = (TA · TB · TC) : (TA' · TB' · TC')
¨

Stelling 2

Een viervlak wordt door elk vlak dat door de middens van twee overstaande ribben gaat, verdeeld in twee delen met gelijke inhoud.

Bewijs:

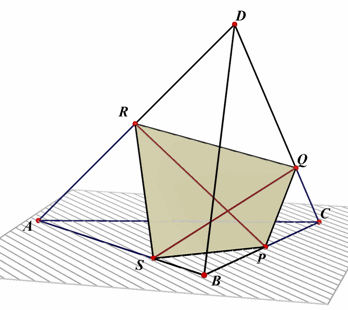P en R zijn de middens van de ribben BC en AD.
Nu is:
Inh(R.ABC) = ¹/₂ Inh(D.ABC)
omdat de hoogte van het eerste viervlak de helft is van die van het tweede, terwijl beide hetzelfde grondvlak hebben.
Verder hebben we:
Inh(ASRQCP) = Inh(R.ABC) + Inh(CPQR) - Inh(BPRS)
Wanneer we nu kunnen bewijzen dat Inh(CPQR) = inh(BPRS) zijn we klaar.

Het lijnstuk PR ligt in het zogenoemde middenvlak (*) van de kruisende lijnen BC en AD.
De lijn PR deelt daardoor het lijnstuk QS middendoor, zodat Opp(PQR) = Opp(PRS).
Uit BP = PC volgt dan verder dat de punten B en C gelijke afstanden hebben tot het vlak PQRS.
De viervlakken CPQR en BPRS hebben dus gelijke grondvlakken en gelijke hoogtes, en dus ook gelijke inhouden.¨

____________
(*) Enkele eigenschappen van het middenvlak worden behandeld in het artikel "Het middenvlak (bij een viervlak)". Dit artikel is opgenomen in een PDF-bestand.
Klik hier om dat bestand te downloaden (PDF-formaat; ca. 330 Kb).

[p : inhviervl.htm] laatste wijziging op: 03-10-2005