Kubus

Overzicht ][ Prisma | Overzicht stereo | Cabri 3D ]

Overzicht

Definitie en eigenschappen
De kubus en andere veelvlakken

¤ Zie eventueel ook de pagina "Stelling van Euler voor veelvlakken".

Definitie en eigenschappen

Definitie
Een kubus is een veelvlak dat gevormd wordt door 6 vierkanten die zo zijn geplaatst, dat ze steeds één zijde (van zo'n vierkant) gemeenschappelijk hebben
of
Een kubus is een rechthoekig blok (parallellepipedum; zie prisma) waarvan de begrenzende vlakken vierkant zijn.

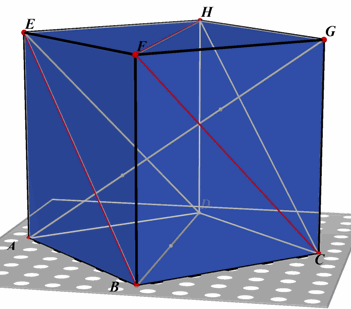Deze gemeenschappelijke zijden (van die vierkanten) worden ribben van de kubus genoemd. Het zijn er ( 6 x 4) / 2 = 12.
Drie van deze ribben komen samen in een hoekpunt. Er zijn dan ( 2 x 12 ) / 3 = 8 hoekpunten.
Verbindingslijnen van hoekpunten (niet zijnde ribben) noemt men diagonalen.
Ligt een diagonaal niet in een zijvlak, dan noemt men zo'n diagonaal lichaamsdiagonaal.

Klik hier >< voor een Cabri 3D applet van de figuur hiernaast (automatisch draaiend; opent in een NieuwVenster).

Stelling
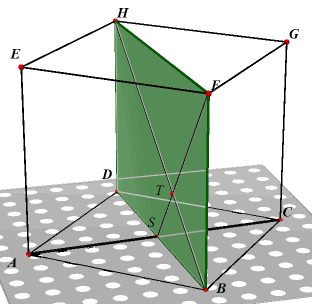
Een lichaamsdiagonaal en een zijvlaksdiagonaal van een kubus die elkaar kruisen, staan loodrecht op elkaar.

Bewijs:
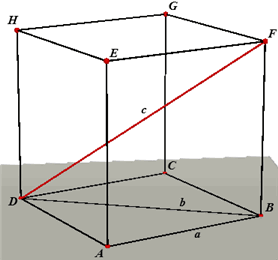
In kubus ABCD.EFGH kruisen de zijvlaksdiagonaal AC en de lichaamsdiagonaal BH elkaar.
Nu is (in vierkant ABCD): AC _|_ BD ......(1)
En omdat BF _|_ ABCD is ook BF _|_ AC ......(2)
Uit (1) en (2) volgt dat AC _|_ vlak BFHD.
En dan staat AC loodrecht op BH.¨

Gevolg 1
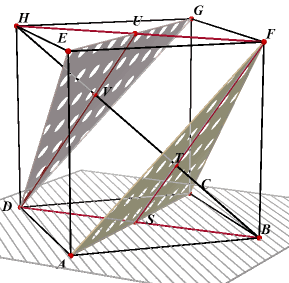
Zo is dus ook BH _|_ AF (en ook BH _|_ CF). Dus BH _|_ vlak AFC en analoog natuurlijk ook BH _|_ EDG.
De vlakken AFC en EDG zijn dus evenwijdig (beide loodrecht op BH).
De vlakken AFC en EDG snijden nu BH in drie gelijke stukken, immers
BS : HF = 1 : 2 = BT : TH
Zodat inderdaad BT = TV = VH.

Gevolg 2
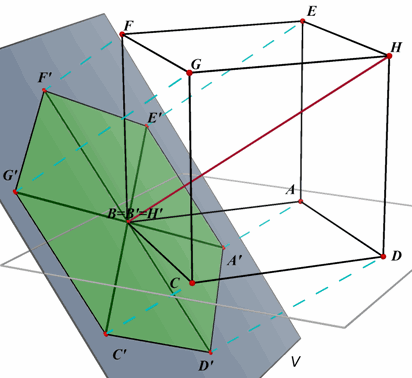
Projecteren we de kubus op een vlak dat loodrecht staat op BH (met projectierichting evenwijdig met BH), dan is de projectiefiguur van de kubus zeshoekig.

In de figuur hiernaast is ABCD.EFGH op deze wijze geprojecteerd op het vlak V door B loodrecht op BH.

Stelling
In een kubus met ribbe a is de lengte van een zijvlaksdiagonaal gelijk aan aÖ2 en die van een lichaamsdiagonaal gelijk aan aÖ3.

Bewijs.
Driehoek ABD is rechthoekig is A. Dus is b = BD = aÖ2 (Stelling van Pythagoras).
Driehoek BFD is rechthoekig in B (BF staat loodrecht op het vlak ABCD).
Dus is:
c = DF = Ö(BD² + BF²) = Ö(2a² + a²) = Ö(3a²) = aÖ3 ¨

De kubus en andere veelvlakken
De kubus kan als 'basis' dienen voor de constructie van enkele andere veelvlakken, zoals:

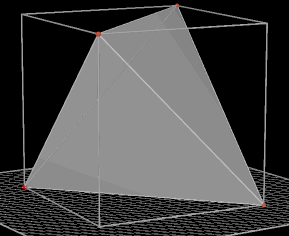Regelmatig viervlak of tetraëder

Het regelmatig viervlak is één van de vijf zogenoemde Platonische lichamen (de kubus zelf behoort daar overigens ook toe.)
Het regelmatig viervlak heeft vier gelijkzijdige driehoek als zijvlakken.

Klik hier >< voor een Cabri 3D applet van nevenstaande figuur (automatisch draaiend; opent in een NieuwVenster).

Constructie: Via 4 hoekpunten van de kubus (zie figuur).

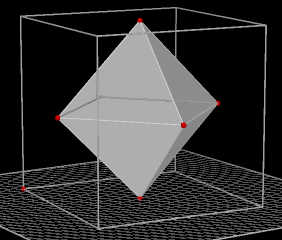Regelmatig achtvlak of octaëder

Het regelmatig achtvlak is ook een Platonische lichaam.
Het regelmatig achtvlak heeft acht gelijkzijdige driehoeken als zijvlakken

Klik hier >< voor een Cabri 3D applet van nevenstaande figuur (automatisch draaiend; opent in een NieuwVenster).

Constructie: Via de 6 middelpunten van de zijvlakken van de kubus (zie figuur).

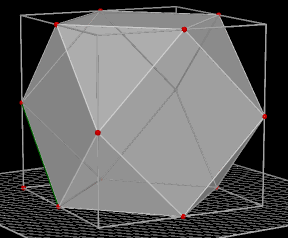Kubo-octaëder

De kubo-octaëder (kuboctaëder) heeft acht gelijkzijdige driehoeken en zes vierkanten als zijvlakken.
De kubo-octaëder is één van de dertien zogenoemde Archimedische lichamen (ook wel half-regelmatige veelvlakken).

Klik hier >< voor een Cabri 3D applet van nevenstaande figuur (automatisch draaiend; opent in een NieuwVenster).

Constructie: Via de 12 middens van de ribben van de kubus.

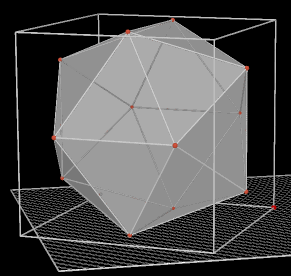
kubus8reg

Regelmatig twintigvlak of icosaëder

Het regelmatig twintigvlak heeft twintig gelijkzijdige driehoeken als zijvlakken.
Ook het regelmatig twintigvlak is een Platonisch lichaam.

Klik hier >< voor een Cabri 3D applet van nevenstaande figuur (automatisch draaiend; opent in een NieuwVenster).

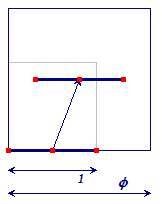
Constructie: Via 6 in de zijvlakken van de kubus gelegen lijnstukken (zie figuur), en wel zo, dat ribbe : lijnstuk = f : 1 , waarbij f (= 1, 61803) het zogenoemde gulden-snede-getal is.

De richtingen van de 6 lijnstukken komen overeen met de drie verschillende richtingen van de kubusribben.

¤ Zie eventueel ook de pagina "Stelling van Euler voor veelvlakken".

[p : kubus.htm] laatste wijziging op: 15-10-2008