Afbeeldingen van het complexe (platte) vlak [3]
0. Overzicht - Eigenschappen van de MŲbius-transformatie
Zie ook de pagina "Complexe getallen en meetkundige bewijzen"
- Het uitgebreide Euclidische vlak, het punt z = •
- Het beeld van een cirkel
- Samenstelling van een M-afbeelding
- Aantal dekpunten en de gevolgen daarvan
- Dubbelverhouding
- De eenheidscirkel
6.1. Het binnengebied van een cirkel
6.2. Het beeld van de eenheidscirkel - Hoektrouw
1. Het uitgebreide Euclidische vlak,
het punt z = •
De MŲbius-afbeelding (M-afbeelding, M-transformatie) f(z) = (az+b)/(cz+d)
met ad-bcĻ 0 kunnen we ook gebruiken om het
Euclidische vlak op zichzelf af te beelden.
Hiertoe denken we het vlak voorzien van een rechthoekig assenstelsel (waarvan de x-as
met de reŽle en de y-as met de imaginaire as samenvalt) en identificeren het
complexe getal z met het punt Z met coŲrdinaten (z1, z2).
We zullen in hetgeen volgt deze beide opvattingen door elkaar gebruiken.
We breiden het Euclidische vlak verder uit, tot wat we noemen het uitgebreide
Euclidische vlak met een punt z = •
dat wordt vastgelegd door de M-afbeelding f(z) = 1/z:
f(O) = •
f(•) = O
O = (0,0) (overeenkomend met het getal z = 0) staat hier voor de oorsprong
van het assenstelsel. We zullen aan het punt z = •
geen coŲrdinaten toekennen.
Ten behoeve van de bewerkingen leggen we vast (definiŽren we) voor ieder complex getal c
(punt):
c Ī • = •
c . •
= •
c / • = 0
c / 0 = •
De uitdrukkingen • - •, • / • en 0 / 0 beschouwen we
als niet-gedefinieerd.
| Stelling 1 Een M-transformatie beeldt een cirkel (of een rechte lijn) af op een cirkel of op een rechte lijn |
Bewijs:
Een rechte lijn of een cirkel in het platte vlak kan worden voorgesteld door | z
- p | = k | z - q | waarbij k een reŽel getal is.
Met andere woorden: we bekijken de verzameling van de punten z waarvoor de
verhouding van de afstanden tot twee vaste punten p en q constant is.
Is k = 1, dan is die verzameling een rechte lijn, de middelloodlijn van het
verbindingslijnstuk tussen p en q.
Is k <> 1, dan is die verzameling de Apollonius-cirkel
bij de punten p en q.
| figuur 1 |  |
figuur 2 | 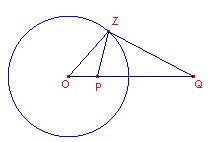 |
Onderwerpen we nu de verzameling aan een M-transformatie Z = (az+b) / (cz+d)
met inverse z = (-dZ+b )/ (cZ-a), dan vinden we
![]()
of
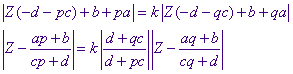
En dit is een vergelijking van de vorm | Z - p' | = k' | Z - q' |.
Dus een rechte lijn of een cirkel. ®
Gevolg
Zijn A en B inverse punten tov. van een cirkel C, dan zijn de M-beelden van A en B elkaars
inverse tov. het M-beeld van C.
Immers p' en q' zijn de beelden van p en q onder
dezelfde M-transformatie.
3. Samenstelling van een M-afbeelding
We bekijken de volgende herleiding:
![]()
We concluderen hieruit, dat iedere M-afbeelding F dus geschrijven kan worden als
F = Ta/c ∑ D ∑ N ∑ Td/c
waarbij
| Td/c | : een translatie over d/c : notatie: z1 = z + d/c |
| N | : de inversie in de eenheidscirkel, gevolgd door een spiegeling in de x-as ; notatie z2 = 1/ z1 |
| D | : een draaivermenigvuldiging met centrum O ; notatie: z3 = (bc-ad)/c2 . z2 |
| Ta/c | : Ta/c : een translatie over a/c ; notatie z' = a/c + z3. |
De afbeelding N, inversie in de eenheidscirkel, gevolgd door spiegeling in de x-as wordt wel de complex-inverse afbeelding genoemd (zie hiervoor ook de pagina "Complex[2]").
Uit deze samenstelling volgt, eveneens, dat lijnen worden afgebeeld op lijnen of cirkels en dat cirkels worden afgebeeld op lijnen en cirkels (zie Stelling 1). De afbeelding N is namelijk de enige van de samenstellende afbeeldingen die van invloed is op de "vorm" van het beeld (zie ook de pagina "Inversie").
4. Het aantal dekpunten en de gevolgen daarvan
| Definitie Onder een dekpunt van een M-afbeelding F verstaan we een punt w met F(w) = w. Een dekpunt wordt dus op zichzelf afgebeeld. |
| Stelling 2 Als een M-afbeelding F drie of meer dekpunten heeft, dan is F de identieke afbeelding. |
Bewijs:
Zij w een dekpunt, dan is w = (aw+b) / (cw+d).
Hieruit volgt dan
cw2 + (d-a)w - b = 0
Heeft deze vergelijking 3 of meer oplossingen, dan moet het de identieke vergelijking
zijn. Met andere woorden:
c = 0, d = a, b = 0.
Uit ad - bc <> 0 volgt in dit geval dat a en d beide ongelijk aan 0 zijn.
De afbeelding z' = (az+b) / (cz+d) gaat nu over in z'
= az / d = z. ®
| Stelling 3 Een M-afbeelding is uniek bepaald door drie punten en hun beeldpunten. |
Bewijs:
Zijn de bedoelde punten zj en zj' (j = 1,2,3).
Zij B de M-afbeelding B: z' = (z - z2)(z1 - z3) / (z - z1)(z2
- z3).
Nu geldt:
B(z1) = •
B(z2) = 0
B(z3) = 1
Zij C de M-afbeelding C: z' = (z - z2')(z1' - z3') / (z -
z1')(z2' - z3')
Onder deze afbeelding geldt
C(z1') = •
C(z2') = 0
C(z3') = 1
We bekijken nu de afbeelding C-1B. Ook dit is een M-afbeelding.
Nu geldt:
C-1B(z1) = z1'
C-1B(z2) = z2'
C-1B(z3) = z3'
Deze afbeelding is uniek. Immers zij A een M-afbeelding met dezelfde eigenschappen, dan is
A-1(C-1B) een afbeelding met drie dekpunten.
Volgens Stelling 1 is dan A-1(C-1B) = I waarbij I
de identieke afbeelding is.
Dus geldt C-1B = A. ®
5. Dubbelverhouding
Op dezelfde wijze als op de pagina "Volledige vierzijde
en dubbelverhouding", maar nu iets anders geschreven, definiŽren we de
dubbelverhouding van vier punten zj (met j = 1,2,3,4).
| Definitie Onder de dubbelverhouding van vier punten zj (j = 1,2,3,4) verstaan we |
Een direct gevolg van deze definitie is de volgende stelling.
| Stelling 4 De dubbelverhouding van vier punten is invariant onder een MŲbius-transformatie. |
Bewijs:
Het bewijs kan worden geleverd door voor de punten zj en zj' = (azj
+ b)/(czj + d) met j = 1,2,3,4 de beide dubbelverhoudingen uit te schrijven.
Directe uitwerking van (z1',z2';z3',z4') geeft
dan het gewenste resultaat. ®
Een belangrijke stelling is
| Stelling 5 De dubbelverhouding van vier verschillende punten is reŽel DESDA De vierpunten liggen op een rechte lijn of op een cirkel. |
Bewijs:
Zijn zj (j = 1,2,3,4) de bedoelde vier punten.
[1] Stel de dubbelverhouding (z1,z2;z3,z4)
= k waarbij k een reŽel getal is.
We moeten nu aantonen, dat de vier punten op een cirkel of op een rechte lijn liggen.
Zij nu F de M-afbeelding die z1, z2, z3 afbeeldt op de
punten z1', z2', z3' van de reŽle as.
Zij verder F(z4) = z4'.
Stelling 4 zegt, dat (z1,z2;z3,z4)
invariant is, zodat ook (z1' - z3')(z2' - z4')
/ (z2' - z3')(z1' - z4') = k.
Waaruit volgt
(z2' - z4') / (z1' - z4') = k
(z2' - z3') / (z1' - z3')
Het rechter lid van deze vergelijking is reŽel, immers zj (j = 1,2,3) is
reŽel.
Lossen we nu de vergelijking op naar z4', dan blijkt, dat z4' = F(z4)
eveneens een reŽel getal is.
De beelden zj (j = 1,2,3,4) liggen dus alle op de reŽle as.
De originelen daarvan liggen dus op een cirkel of op een rechte lijn, namelijk op het
beeld onder F-1 van de as.
[2] Liggen nu de punten zj (j = 1,2,3,4) op een cirkel of op
een rechte lijn.
Er is nu een M-afbeelding G, die z1, z2, z3 afbeeldt op z1',
z2', z3' van de reŽle as (volgens stelling 3).
Ook z4' ligt op de reŽle as, immers G beeldt de cirkel of rechte lijn af op
een rechte lijn.
De dubbelverhouding (z1',z2';z3',z4') is dus
gelijk aan een reŽel getal. Volgens stelling 4 is dus ook de
deelverhouding (z1,z2;z3,z4) een reŽel getal.®
Opmerking
Van Stelling 5 wordt veelvuldig gebruik gemaakt bij het
bewijzen van meetkundige eigenschappen met behulp van complexe getallen.
Zie daarvoor de pagina "Complexe getallen en
meetkundige bewijzen".
[einde Opmerking]
6.1. Het binnengebied van een cirkel
| Stelling 6 Wordt een cirkel C afgebeeld door een M-transformatie op een cirkel C', dan wordt het binnengebied van C afgebeeld op het binnengebied van C' of op het buitengebied van C'. |
Bewijs:
Uit de samenstelling van de algemene M-transformatie (zie paragraaf 3)
blijkt dat alle deeltransformaties, met uitzondering van de inversie, het binnengebied van
een cirkel afbeelden op het binnengebied van de beeldcirkel.
De inversie beeldt het binnengebied af op het binnengebied of op het buitengebied van de
beeldcirkel; een en ander is afhankelijk van de ligging het centrum C van de inversie tov.
de cirkel (het origineel):
a. centrum binnen het origineel: beeld van het binnengebied is het buitengebied
van de beeldcirkel (zie figuur 3);
b. centrum buiten het origineel: beeld van het binnengebied is het binnengebied
van de beeldcirkel (zie figuur 4).
| figuur 3 | 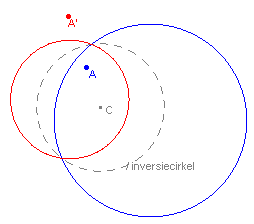 |
figuur 4 | 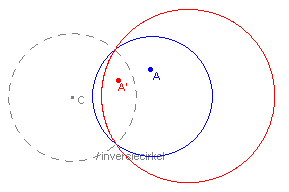 ® ® |
6.2. Het beeld van de eenheidscirkel
We leiden hieronder af aan welke voorwaarden een M-transformatie moet voldoen om de
eenheidscirkel (niet puntsgewijs) op zichzelf af te beelden, waarbij tevens
het binnengebied (niet puntsgewijs) op zichzelf wordt afgebeeld.
Voor een punt z = (p, q) = p + qi op de eenheidscirkel
geldt p2 + q2 = 1 of ook z . z_
= 1 (hierbij is z_ de geconjugeerde van z).
Voor het beeld Z van z bij de afbeelding Z = (az + b) / (cz + d) moet dus gelden
Z . Z_ = 1.
Het beeld van Z . Z_ = 1 volgt uit:
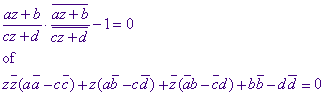
Dit is dezelfde vergelijking als z . z_ - 1 = 0, indien
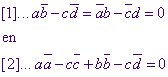
We hebben dus de volgende twee voorwaarden:
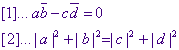
Uit [1] kunnen we afleiden, c = a/d_ . b_. Stellen we k =
a/d_, dan is dus d = a_/k_.
Substitutie hiervan in [2] geeft dan
![]()
Dus is | k | = 1. In dit geval is 1/k_ = k
De vorm van de M-transformatie is dan dus ![]()
Dit kunnen we natuurlijk ook schrijven als
![]()
Deze afbeelding beeldt de eenheidscirkel op zichzelf af.
We moet vervolgens nog onderzoeken onder welke voorwaarde het binnegebied op zichzelf
wordt afgebeeld.
Het is voldoende dit te onderzoek voor ťťn punt van het binnengebied.
We kiezen z = 0.
Nu is Z = k ∑ b/a_. Moet nu gelden dat |Z| < 1, dan hebben
we |k|.|b| / |a_| < 1. Wegens |k|
= 1 moet gelden:
|b| < |a_|. En daar |a|=|a_| is de voorwaarde |b| < |a|.
Aan deze voorwaarde is (ondermeer) voldaan indien |a|2 - |b|2
= 1.
We kunnen nu eenvoudig afleiden:
| Stelling 7 De afbeelding Z = K (z - m) / (1 - m_z) met |K|=1 en |m| < 1 beeldt de eenheidscirkel opzichzelf af, waarbij het binnengebied op het binnengebied wordt afgebeeld. |
Bewijs:
Uitgaande van Z = (az + b) / (b_z + a_) met
|b| < |a| vinden we bij deling door a_ dat
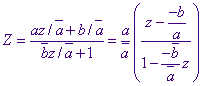
Nu is |a/a_| = 1.
Stellen we K = a/a_ en m = -b/a, dan is dit te schrijven als Z
= K(z - m) / (1 - m_z), waarbij |K|=1 en |m|<1.
®
Opmerkingen
[1]
Het bijzondere van deze afbeelding is, dat z = m op z = 0 wordt
afgebeeld.
[2]
Voor eenvoudige beschouwingen kunnen we K = 1 gebruiken.
[einde Opmerkingen]
7. Hoektrouw
Een belangrijke eigenschap van de M-afbeelding is dat de hoek tussen twee rechte lijnen
gelijk is aan de hoek tussen de beelden van die rechte lijnen (bij M-afbeeldingen zijn die
beelden dus in het algemeen cirkels; zie Opmerking hierna).
Een afbeelding die de grootte van de hoek tussen twee lijnen invariant laat noemt men een conforme
afbeelding. Zo'n afbeelding heet ook wel hoektrouw.
We hebben dus:
| Stelling 8 Een M-afbeelding is een conforme afbeelding. |
Bewijs:
Een M-afbeelding is opgebouwd uit twee translaties, een draaivermenigvuldiging en een
complex-inverse afbeelding (zie paragraaf 3).
Een translatie en een draaivermenigvuldiging zijn inderdaad conform (eigenschappen uit de
Euclidische meetkunde).
De complex inverse afbeelding bestaat uit een inversie en een spiegeling.
Ook de spiegeling is hoektrouw.
De inversie is eveneens een conforme afbeelding. Zie de pagina "Inversie" voor het bewijs daarvan.
Uit de samenstelling van de M-afbeelding volgt dus, dat deze hoektrouw is. ®
| figuur 5 | 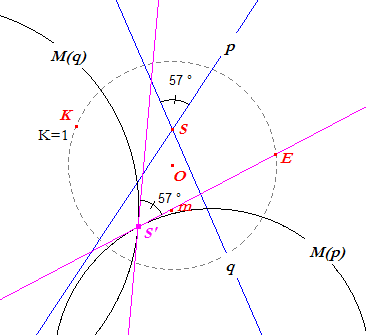 |
Opmerking De hoek tussen twee cirkels wordt gedefinieerd als de hoek tussen de raaklijnen in een raakpunt aan die cirkels. [einde Opmerking] Hiernaast zijn de beelden M(p) en M(q), cirkels,
getekend van de lijnen p en q onder de M-afbeelding |
[complex3.htm] laatste wijziging op: 02-12-2008 (26-02-2002)