Afbeeldingen van het complexe vlak [2]

Overzicht ][ Complex [1] | Julia-set | Mandelbrot-set | Fractalen ][ Meetkunde

Begin

0. Overzicht

Som, product, kwadraat
Overige standaard afbeeldingen, macro's
2.1 tm. 2.6 (overzicht afbeeldingen)
Voorbeelden
     3.1. Veelterm-functies
     3.2. Rotatie
     3.3. Omgekeerde
     3.4. Möbius-transformatie
Download

1. Som, product, kwadraat
De afbeeldingen som, product en kwadraat zijn behandeld op de pagina "Complex [1]".
Voor deze afbeeldingen bestaan macro's: CSom, CProduct en CKwadraat.

2. Overige standaard afbeeldingen, macro's
We behandelen op deze pagina de volgende afbeeldingen van het complexe vlak

2.1. Verschil
2.2. Inverse
2.3. Quotiënt
2.4. Invers-geconjugeerde
2.5. Algemene Möbius-transformatie
2.6. Animatie

2.1. Verschil
Bij deze constructie wordt gebruik gemaakt van de macro:CSom. Deze macro is gebaseerd op de constructie van de som van twee complexe getallen.
De help-tekst bij deze macro luidt:
"Complexe som (Z1+Z2)
- Selecteer Z1, Z2 en O (in deze volgorde)"

verschil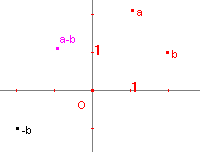

Gegeven:
  complexe getallen a en b en het punt O
Te construeren:
  a - b
Constructie:
  -b = Puntspiegeling(b, O)
  a - b = CSom(a, -b, O)

Op deze constructie is de macro:CVerschil gebaseerd.
De helptekst bij deze macro luidt:
"Complex verschil (Z1-Z2)
- Selecteer Z1, Z2 en O (in deze volgorde)"

2.2. Inverse
Onder de inverse van een complex getal z verstaan we het complexe getal 1/z.
Bij deze constructie is het noodzakelijk, naast de oorsprong, een eenheid in het complexe vlak vast te leggen. We gebruiken hiervoor een punt E.
De bedoelde eenheid is dan de lengte van het lijnstuk OE.
In de figuren wordt vaak ook de eenheidscirkel (O, OE) getekend, maar deze is voor de constructies met Cabri in het complexe vlak niet noodzakelijk.

inverse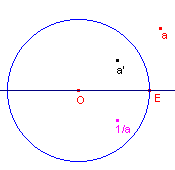

Gegeven:
  het complexe getal a en de punten O en E
Te construeren:
  1/a
Constructie:
We tekenen eerst de cirkel met middelpunt O die door E gaat (inversie-cirkel) en de lijn door O en E.
  a' = Inversie(a, cirkel)
  1/a = Spiegeling(a', lijn OE)

Op deze constructie is de macro:CInverse gebaseerd.
De helptekst bij deze macro luidt:
"Complexe inverse van Z
- Selecteer Z, O en E (in deze volgorde)"
Mogelijk dat de naamgeving van afbeelding cq. macro wat verwarrend werkt. Ook de term omgekeerde (of reciproke) wordt wel voor deze afbeelding gebruikt.

2.3. Quotiënt
Bij deze constructie maken we gebruik van de macro:CInverse en de macro:CProduct. Zie voor deze laatste macro de pagina Complex [1].

quotient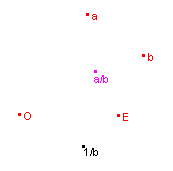

Gegeven:
  de complexe getallen a en b en de punten O en E
Te construeren:
  a/b
Constructie:
  1/b = CInverse(b, O, E)
  a/b = CProduct(a, 1/b, O, E)

Op deze constructie is de macro:CQuotient gebaseerd.
De helptekst bij deze macro luidt:
"Complex quotient van Z1 en Z2
- Selecteer Z1, Z2, O en E (in deze volgorde)"

2.4. Invers-geconjugeerde
Onder de invers-geconjugeerde van het complexe getal z verstaan we het complexe getal 1/z_.
Om technische redenen schrijven we hier z_ in plaats van waarbij z = a + bi.

iconjug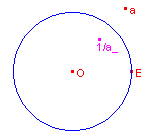

Gegeven:
  het complexe getal a en de punten O en E
Te construeren:
  1/a_
Constructie:
We tekenen eerst de cirkel (O, OE)
  1/a = Inversie(A, cirkel)

De invers-geconjugeerde van een complex getal z is dus de inverse (via Inversie) van het Cabri-punt ten opzichte van de eenheidscirkel.

Op deze constructie is de macro:CIconjug gebaseerd.
De helptekst bij deze macro luidt:
"Complex invers-geconjugeerde van Z
- Selecteer Z, O en E (in deze volgorde)"

2.5. Algemene Möbius-transformatie
De Möbius-transformatie van het complexe vlak heeft de vorm en ad - bc ¹ 0.

We kunnen met gebruikmaking van de macro's CProduct, CSom (zie hiervoor de pagina "Complex [1]") en CQuotient de Möbius-transformatie bij gegeven complexe getallen a, b, c en d eenvoudig opbouwen.

mobius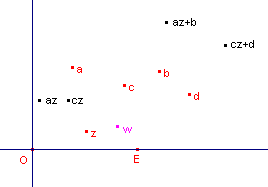

Gegeven:
  de complexe getallen a, b, c, d en de punten O en E
Te construeren:
  w = (az+b)/cz+d)
Constructie:
  az = CProduct(a,z,O,E)
az+b = CSom(az, b, O)
cz = CProduct(c,z,O,E)
cz+d = CSom(cz,d,O)
w = CQuotient(az+b,cz+d,O,E)

Op deze constructie is de macro:CMobius gebaseerd.
De helptekst bij deze macro luidt:
"Mobius-beeld van Z
- Selecteer Z, a, b, c, d, O en E (in deze volgorde)"

Opmerking
Het gebruik van deze macro is omslachtig.
Soms ook is het, vanwege een beperking in Cabri, zelfs niet (direct) mogelijk de macro te gebruiken (indien namelijk een punt twee of meer keer zou moeten worden gebruikt).
Het verdient daarom verre de voorkeur Möbius-transformaties samen te stellen met de andere standaard afbeeldingen en soms ook gebruik te maken van de eigenschappen van complexe getallen.
[einde Opmerking]

2.6. Animatie
Van de standaard afbeeldingen (muv. de Möbius-transformatie) is hieronder een animatie beschikbaar.
Klik hier voor het starten van die animatie.

3. Voorbeelden
3.1. Veeltermfuncties
Op de pagina Complex [1] zijn voorbeelden gegeven van een afbeelding toegepast op de Mandelbrot-verzameling, nl. via de functie f(z) = z² + c.
Hieronder staan twee voorbeelden van een algemene veeltermfunctie van de 2e graad en van de 3e graad
(met dank voor deze voorbeelden aan Leroy J. Dickey, University of Waterloo, Canada).
Verder is een voorbeeld opgenomen over eenheidswortels.

3.1.1. Algemene complexe polynomen

figuur 1.1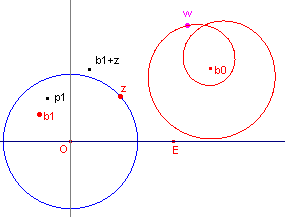

De gebruikte functie in figuur 1.1 is
w = f(z) = b₀ + b₁z + z² = b₀ + z(b₁ + z).

In de figuur is
p₁ = z(b₁ + z).
Met behulp van het punt z op een cirkel met O als middelpunt is de meetkundige plaats van het beeld w van z bepaald.

Opmerking
Functies als g(z) = a + z zijn translaties.
[Einde Opmerking]

Klik hier

voor een animatie van figuur 1.1.

figuur 1.2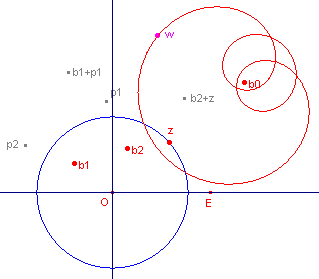

De gebruikte functie in figuur 1.2 is
w = f(z) = b₀ + b₁z + b₂z² + z³ = b₀+z(b₁+z(b₂+z)).

In de figuur is
p₁ = z(b₂+z) en p₂ = z(b₁+p₁).
Met behulp van het punt z op een cirkel met O als middelpunt is de meetkundige plaats van het beeld w van z bepaald.

Klik hier

voor een animatie van figuur 1.2.
3.1.2. Eenheidswortels

figuur 1.3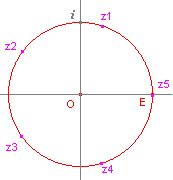

In figuur 1.3 zijn de complexe eenheidswortels van de vergelijking z⁵ = 1 weergegeven.
Constructie:
  z = z1
  z2 = CKwadraat(z1, O, E)
  z3 = CProduct(z1, z2, O, E)
  z4 = CKwadraat(z2, O, E)
  z5 = CProduct(z2, z3, O, E)

Klik hier

voor een animatie van figuur 1.3.

3.2. Rotatie
We beschouwen nu de functie w = f(z) = az, waarbij |a|=1 (dwz. a ligt op de eenheidscirkel).
We kunnen aannemelijk maken, dat deze functie een rotatie is (in het geval dus, dat |a|=1). Zie hiervoor figuur 2.1.

figuur 2.1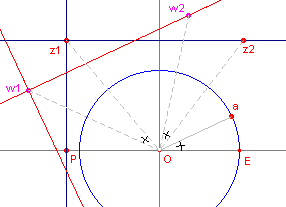

De rotatie hoek is gelijk aan hoek (aOE).
In de figuur zijn de lengtes van de lijnstukken z₁z₂ en w₁w₂ aan elkaar gelijk.

Opmerking
Is |a| ongelijk aan 1, dan is de afbeelding een draaivermenigvuldiging.
[einde Opmerking]

Klik hier

voor een animatie van figuur 2.1.

3.3. Omgekeerde
We beschouwen de functie w = f(z) = 1/z .Dit is dus de inverse (omgekeerde, reciproke) functie.
Deze functie is een Möbius-transformatie met a = 0, b = 1, c = 1 en d = 0.

figuur 3.1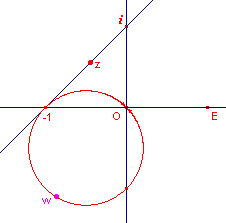

In figuur 3.1 is het beeld getekend van de lijn door de punten 1 en i. Het beeld is een cirkel door het punt O.

We kijken vervolgens naar het beeld van de lijnen die loodrecht op deze lijn staan.
Daartoe tekenen we in z een loodlijn (zie figuur 3.2).
Op deze lijn kiezen we een punt z1.
De "meetkundige plaats" van het beeld w1 van z1 is dan het beeld van de betreffende loodlijn. Het is eveneens een cirkel die door het punt O gaat.

Via de Spoor-optie van Cabri kunnen we nu de beelden tekenen van een aantal van deze loodlijnen. Zie daartoe figuur 3.3.

Klik hier

voor een animatie van figuur 3.1.

figuur 3.2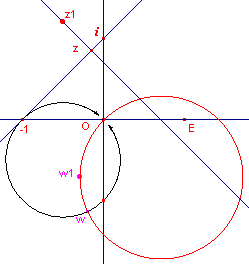

figuur 3.3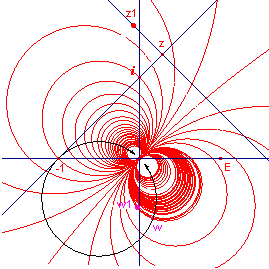

Klik hier

voor een animatie van figuur 3.2.

Opmerking
Deze cirkels snijden de eerste cirkel (zie ook figuur 3.2) loodrecht.
Dit is gelegen in het feit, dat een Möbius-transformatie een conforme (hoektrouwe) afbeelding is.
[einde Opmerking]

figuur 3.4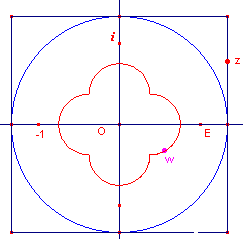

In figuur 3.4 is het beeld onder w = f(z) = 1/z getekend van een vierkant om de oorsprong.
Het binnengebied van het vierkant wordt afgebeeld op het buitengebied van het beeld van het vierkant (zie daarvoor de animatie).

Klik hier

voor een animatie van figuur 3.4

3.4. Möbius-transformatie
We beschouwen tenslotte de functie w = f(z) = (z + i) / (z - i).
Ook dit is een Möbius-transformatie.
Deze afbeelding kan worden samengesteld met de macro's CSom (zie de pagina Complex [1]) en CQuotient.

figuur 4.1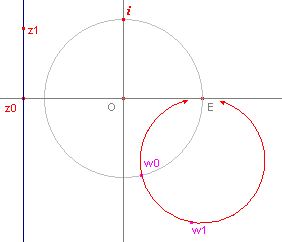

In figuur 4.1 is het beeld getekend van de loodlijn in z0 op de reële as (als meetkundige plaats van w1, het beeld van z1).
Het beeld is een cirkel die door E gaat (E is het beeld van het oneigenlijk punt van de loodlijn).
Het beeld van z0 ligt op de eenheidscirkel, immers, voot z0 = a (reëel) vinden we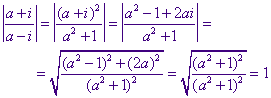
complex2complex4f

waarbij er telkens weer sprake is van loodrechte snijding van beeldcirkel en eenheidscirkel.

Klik hier

voor een animatie van figuur 4.1.

figuur 4.2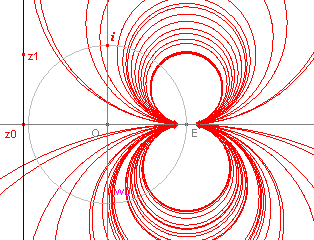

De beelden van lijnen loodrecht op de reële as vormen dus een bundel van cirkels die in E raken aan de x-as (zie figuur 4.2).
Het beeld van de "lijn op oneindig" is de x-as zelf.

Opmerking
De beelden van de lijnen loodrecht op de imaginaire as vormen een cirkelbundel waarvan de elementen in E raken aan de eenheidscirkel.
(niet getekend).
[einde Opmerking]

figuur 4.3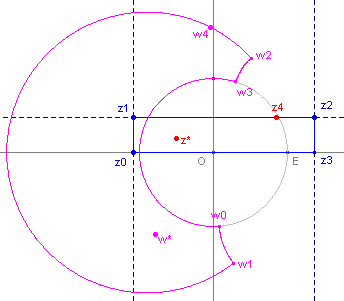

In figuur 4.3 is het beeld getekend van de rechthoek ("contour" ) bepaald door de punten z0, z1, z2, z3.
Het punt z4 doorloopt deze rechthoek. De meetkundige plaats van het punt w4 is het beeld van de rechthoek.

Het punt z* (met beeld w*) is een willekeurig punt.
Het binnengebied van de rechthoek wordt (zoals we kunnen zien aan de ligging van w*) afgebeeld op het binnengebied van het beeld van de rechthoek.

Klik hier

voor een animatie van figuur 4.3.

4. Download
De hierboven behandelde figuren kunnen in een bestand via deze website worden gedownload.
In het bestand zijn ook de macro's en enkele niet behandelde figuren opgenomen, alsmede het bestand complex.men, waarmee alle macro's tegelijk kunnen worden geladen.
Klik hier om het downloaden te starten [ZIP-bestand, 33Kb].

Opmerking
De definitie van de in het bestand opgenomen macro's CSom, CProduct en CKwadraat wijken enigszins af van de definities van de macro's die gebruikt zijn op de pagina "Complex [1]".
[einde Opmerking]

Begin

[complex2.htm] laatste wijziging op: 27-12-2004