Mandelbrot-fractaal
Overzicht ][ J-fractaal | Complexe afbeeldingen | Fractalen
1. Inleiding
Evenals bij de Julia-fractaal, wordt voor het
generen van de Mandelbrot-fractaal uitgegaan van de functie
f(z) = z2 + C
die de punten van het complexe vlak afbeeldt op zichzelf.
Nu wordt als startpunt van het iteratie proces steeds z0 = 0 genomen
en wordt gekeken naar de waarden van C die leiden tot convergentie en divergentie van het
iteratie proces.
De Mandelbrot-verzameling bestaat uit die punten C (in het complexe
vak) waarvoor het iteratie proces zn+1 = zn2 + C (met z0 = 0)
convergent is.
De rand van het "begrensdheidsgebied" is weer een fractaal, de Mandelbrot-fractaal.
Een van de eigenschappen van de Mandelbrot-verzameling (M-set) is, dat voor elk punt van de M-set de bijbehorende Julia-set "samenhangend" is.
 |
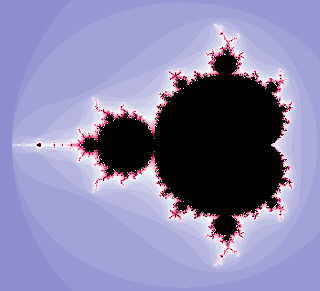Hiernaast is de Mandelbrot-set getekend (als het zwarte gebied). En ook nu is gebruik gemaakt van kleuren die bepaald worden door de "snelheid" van divergentie van het betreffende punt. Het "niervormige" gedeelte van de
M-set is een zogenoemde cardioïde (hartlijn) met middelpunt (0 ; 0). Kortom: de M-set wordt begrensd door een fractaal: |
Hieronder staan nog een tweetal details van de M-verzameling.
 |
 |
Mandelbrot (Benoit Mandelbrot, 1924-..., Polen) ontdekte de M-set en de daarmee
samenhangende M-fractaal door bij elke Julia-set het punt C ter markeren waarvoor de
Julia-set samenhangend was.
Dit lijkt op het eerst gezicht nogal omslachtig, maar Julia had bij zijn onderzoek (zonder
de set zelf te tekenen!) al ontdekt, dat het voldoende was de "baan" van punten
in het iteratie proces uitgaande van het punt C te onderzoeken.
Gaat die baan naar oneindig, dan is de Julia-set bij die bij deze C behoort. niet
samenhangend.
Mandelbrot was als eerste in staat de bijbehorende sets met behulp van een computer te
tekenen.
Hij publiceerde zijn resultaten in zijn boek "Les objets fractals, form, hasard et
dimension" (1975) en meer uitgebreid in "The fractal geometry of nature"
(1982).
2. Z-banen
Met behulp van een computerprogramma kunnen de banen die door het iteratie proces zn+1
= zn2 + C worden bepaald, voor de verschillende (complexe)
waarden van C worden getekend.
Ook deze banen hebben bij convergentie een bijzondere gedaante.
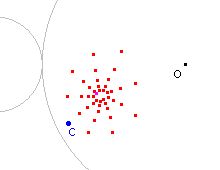
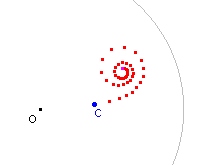
Hieronder staan twee van dit soort banen die met het programma Cabri Geometry zijn geconstrueerd.
 |
 |
|
| C = (-0,61 ; -0,41) | C = (0,28 ; 0,03) |
Als referentie zijn in bovenstaande figuren een cirkel met middelpunt
O en straal ½ getekend. Het eerste punt van de serie is dus steeds het punt z0
= 0 met als tweede punt het punt C.
Het laatste geconstrueerde punt in de baan heeft een afwijkende kleur (paars).
 |
Ophalen van de figuur in Cabri Geometry |  |
Animatie met CabriJava | (*) |
| (*) | Voor het ophalen van de figuur in Cabri
Geometry (indien deze niet in een ZIP-bestand is opgenomen) is het
noodzakelijk dat Cabri II is geïnstalleerd op
het gebruikte computersysteem, waarbij de Map-opties voor "Cabri-géomètre II
Figure" en "Cabri-géomètre II Macro" op de juiste wijze zijn ingesteld. Voor animaties met CabriJava moet de gebruikte browser in staat zijn Java-applicaties uit te voeren. Is dit niet het geval, dan kunnen de figuren ook worden gedownload via deze website (zie hiervoor Download). |
| . |
 |
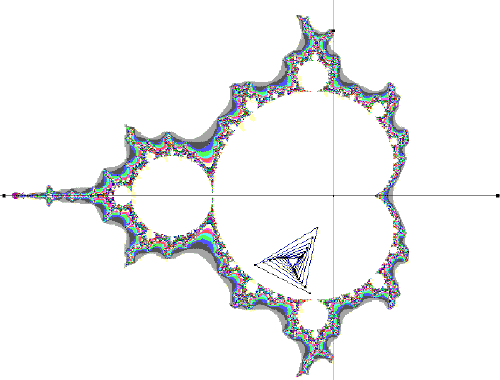Hiernaast staat een schermafdruk van een Cabri-figuur uit CabriPlus. In CabriPlus is het mogelijk een afbeelding in de achtergrond op te nemen (zoals in dit geval de M-verzameling zelf, gemaakt met een fractal-generator). Klik
hier >
Met dank aan: Koen Stulens (Limburgs Universitair Centrum, Diepenbeek, België) |
Zie ook de pagina's "Afbeeldingen van het complexe vlak" voor de basisconstructies die hierbij gebruikt zijn.
3. M-bollen,
periode
Het hartvormig deel van de M-set heeft aan de rand grote (waaronder de
linker cirkel) en kleinere uitstulpingen. Deze uitstulpingen heten Mandelbrot-bollen
(M-bollen).
Punten binnen zo'n M-bol hebben alle een bijzondere eigenschap.
Deze eigenschap illustreren we aan de hand van het punt C = i.
De baan die bij deze waarde van C hoort is:
0 ® i ® -1 + i ®
-i ® -1 + i
® -i ®
...
We noemen deze baan een 2-cyclus.
 |
Het blijkt dat de baan, uitgaande van het punt 0, voor elk punt binnen
een M-bol wordt aangetrokken tot een n-cyclus. Elke M-bol kan daardoor worden gekarakteriseerd door een getal n (de periode van de M-bol). In de figuur hiernaast staan de perioden van de (primaire) M-bollen. |
De periode n van een M-bol blijkt dan ook weer terug te komen in de samenhang met de bij zo'n punt C behorende Julia-fractaal.
 |
In deze figuur staat de Julia-verzameling van het punt C = (-0,122 ;
0,744). Deze Julia-verzameling heet het "konijn van Douady". De verzameling bestaat uit een centraal deel waaraan twee "oren" zitten. Bekijken we zo'n oor, dan zijn ook daaraan weer twee andere te onderscheiden. De verzameling is op te vatten als een oneindig aantal punten die elk het hoekpunt zijn van 3 verschillende delen van de Julia-verzameling. Dat het juist 3 delen zijn, wordt veroorzaakt door het feit, dat C in een M-bol ligt met periode 3 (de bovenste). |
Voor enkele wiskundige overwegingen hierbij zie de pagina's "Afbeeldingen van het complexe vlak".
5. Download
De hierboven behandelde Cabri-figuur (Z-banen) kan ook in een bestand via
deze website worden gedownload.
Dit bestand bevat ook de macro's die op de constructies van "som",
"product" en "kwadraat" zijn gebaseerd (zie de pagina's "Afbeeldingen") en die zijn gebruikt bij het tekenen van de
Z-banen.
Klik hier om het downloaden te
starten [12,5 Kb, ZIP-formaat].
[mandelbrot.htm] laatste wijziging op: 25-06-2003