Julia-fractaal

Overzicht ][ M-fractaal | Complexe afbeeldingen | Fractalen

0. Overzicht

De functie f(x) = x² + C
Iteratief gedrag van x_n+1 = x_n² + C
Julia-set (-verzameling)
Enkele kleurige voorbeelden

1. De functie f(x) = x² + C
We bekijken deze functie op een bijzondere manier: we maken een rij van functiewaarden als volgt.

Kies een getal, en noem dat x₀.
Bereken de functiewaarde voor x₀, en noem deze waarde x₁.
Bereken de functiewaarde voor x₁, en noem deze waarde x₂.
Enzovoorts.

We krijgen dus een rij getallen die voldoen aan x_n+1 = f(x_n).

Gaston Julia (Gaston Maurice Julia, 1893 - 1978, Frankrijk) publiceerde in 1919 zijn boek Mémoire sur l'iteration des fonctions rationelles waarin hij het iteratief gedrag van de in hoofde genoemde functie(s) onderzocht.

C = 0
Voor c = 0 hebben we uitgaande van verschillende waarden van x₀ ook verschillende rijen met een verschillend gedrag:
[1]   x₀ = 0, x₁ = 0, x₂ = 0, x₃ = 0, ...
[2]   x₀ = 1, x₁ = 1, x₂ = 1, x₃ =1, ...
[3]   x₀ = 2, x₁ = 4, x₂ =16, x₃= 256, ...
[4]   x₀ = 0,7 ; x₁ = 0,49 ; x₂ = 0,2401 ; x₃ = 0,057648 ; x₄ = 0,003323 ; x₅ = 0,000011 ; ...
[5]   x₀ = 1,1 ; x₂ = 1,21 ; x₃ = 1,4671 ; x₄ = 2,14359 ; ...
We zien, dat de rijen [1], [2] en [4] convergeren.
De rijen [3] en [5] divergeren.

C ¹ 0
De relatie x_n+1 = x_n² + C met C ¹ 0 vertoont echter een wat afwijkend iteratief gedrag.
Hieronder staat een tabel met verschillende waarden van C (horizontaal) bij 30 iteraties (vertiicaal).

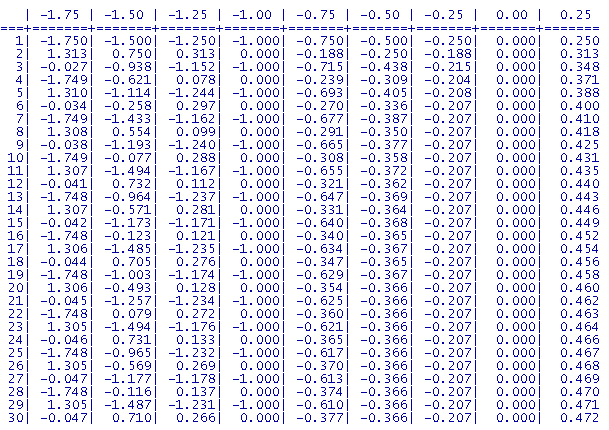
juliatabel

Hierin is zijn al wat bijzonderheden te ontdekken.
Voor de gebruikte waarden van C groter dan -0,75 en kleiner dan 0,25 convergeert het iteratieproces.
Maar nemen we kleinere waarden dan -0,75 (zie bijvoorbeeld C = -1,75) dan treedt zelfs periodiciteit op.

In paragraaf 2 zullen we iteratieve gedrag van de functie f(x) = x²+ C voor verschillende waarden van C nader (grafisch) onderzoeken.
Zie voor een overeenkomstige functie de pagina "Logistische functie".

2. Iteratief gedrag van x_n+1 = x_n² + C

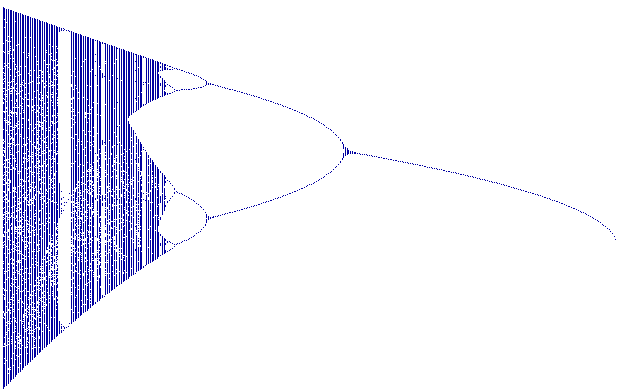
bifurc

Bovenstaande figuur geeft grafisch het iteratie proces weer, waarbij telkens x₀ = 0 en C varieert van -2 (geheel links) tot 0,25 (rechts in de figuur).
Het computerprogramma waarmee bovenstaande tekening is gemaakt, berekent 1000 iteraties voor 360 waarden van C. Blijkbaar worden in de figuur links alle waarden tussen twee grenzen aangenomen. Verder naar rechts gaand neem het aantal "stationaire" punten af via vier en twee naar één waarde (in dit laatste geval is er dus sprake van convergentie).

3. Julia-set (-verzameling), Julia-fractaal
Wanneer we de relatie z_n+1 = z_n² + C bekijken in het complexe vlak, waarin z = x + yi, dan kunnen we via de functie f(z) = z² + C de punten van het complexe vlak op elkaar afbeelden.
Voor de constructie van de Julia set bij een bepaalde C wordt de rij
z₀, z₁, z₂, z₃, ...
bekeken.
Blijft deze rij begrensd, dan wordt het startpunt z₀ geplot.
De Julia-set bij C bestaat uit alle punten z₀ waarvan het proces z_n+1 = z_n² + C begrensd is.

Er zijn op basis hiervan twee verzamelingen te construeren:
- de verzameling van de punten z₀ waarvoor het itertieve proces begrensd is (de Julia-set bij C)
- de verzameling van de punten z₀ waarvoor de verzameling niet-begrensd is.

De rand van het "begrensdheidsgebied" wordt een "fractaal" genoemd, de Julia-fractaal bij C.

Overigens kan bewezen worden, dat de punten C waarvoor er een "gesloten" Julia-fractaal bestaat, tot een wel-gedefinieerde verzameling behoren: de Mandelbrot-verzameling genoemd naar Benoit Mandelbrot (1924-..., Polen) die het begrip "fractaal" in 1977 introduceerde.

Opmerking
Als we een punt Z in het complexe vlak weergeven met Z = (x,y) en als C = (a,b), dan wordt Z dus afgebeeld op

Z' = $fractimsjulia_f1$

Voor het beeldpunt Z' van Z vinden we dus Z' = (x', y') = ( x² - y² + a, 2xy + b)
Zonder verder iets van complexe getallen af te weten, kunnen we dus ook de afbeelding

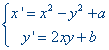
$fractimsjulia_f2$

bekijken.
[einde Opmerking]

Uiteraard is voor dit type constructies een computer onmisbaar.
Een enkele (zeer) eenvoudige Julia-set is echter ook wel zonder computer te tekenen.

C = (0 ; 0)
We hebben nu dus de functie f(z) = z², waarvoor we alle mogelijke rijen op begrensdheid willen onderzoeken.
   z₀ = 0 geeft de rij 0, 0, ...
   z0 = 1 geeft de rij 1, 1, ...
   z0 = -1 geeft de rij -1, 1, 1, ...
   z0 = i geeft de rij i, -1, 1, ...
   z0 = -i geeft de -i, 1, 1, ...

We hebben nu dus al 5 punten van de Julia-set voor C = (0 ; 0) gevonden.
Ook de delen van de assen tussen de genoemde punten behoren ertoe.
En het gebied binnen de eenheidscirkel, immers de daarbij behorende rijen convergeren alle naar 0.
Echter de punten buiten de eenheidscirkel divergeren.
De Julia-fractaal bij C = (0 ; 0) is dus de eenheidscirkel.
De Julia-set bij C=0 is dus de "gevulde" eenheidscirkel.

Hiernaast staat de Julia-set voor C = (0,25 ; 0).

4. Enkele kleurige voorbeelden
De Julia-sets (-fractalen) geven aanleiding tot vele fraaie plaatjes, zeker wanneer men er kleuren aan toevoegt.
De in onderstaande sets gebruikte kleuren zijn afhankelijk van het aantal voor divergentie of convergentie benodigde iteraties.

	In deze figuur staat de fractaal voor C = (0,75 ; 0). Mandelbrot was een der eersten die dit plaatje verkreeg. Het deed hem denken aan de beroemde San-Marco-kerk, weerspiegeld in het ondergelopen San-Marco-plein in Venetië.
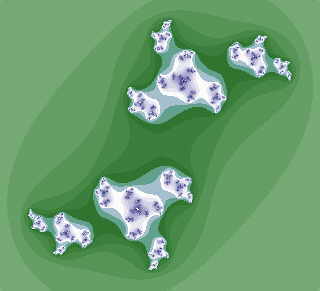	Deze figuur geeft de fractal voor C = (0,1 ; -0,8) weer. Het valt wellicht op, dat de figuur niet meer samenhangend is, maar uit losse punten bestaat. Een dergelijke fractal pleegt men als "Fatou-stof" te beschrijven. Dit ter ere van de wiskundige Fatou, een tijdgenoot van Julia (Pierre Josph Louis Fatou, 1878-1929, Frankrijk).
	De fractal hiernaast is die van C = (0 ; 1). Een dergelijke fractaal wordt wel "dendriet" genoemd.

Vervolgens nog twee die zijn enigszins zijn uitvergroot.


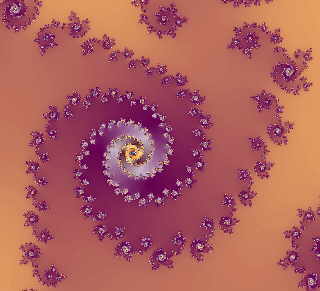C = (-0,21 ; -0,67)		C = (0,23 ; -0,6)

[julia_fractaal.htm] laatste wijziging op: 29-03-2000