De logistische functie (1)
Definitie | Iteraties | Verloop ][ De logistische functie (2) ][ DK & Maple
Een beschrijving van de logistische functie
met gebruikmaking van het computerprogramma Maple V, release 4
maart 1998
(Literatuur: Chaos, CWI-syllabus 1997)
1. Definitie
We geven allereerst de definitie van de logistische functie op
het interval [0 ; 1] met l in [0 ; 4] via een aantal
Maple-commando's
> restart:
> with(plots):
> f := x -> l*x*(1-x);f := x -> l x (1 - x)
> lambda := 4;
l := 4
> plot(f(x), x=0..1);
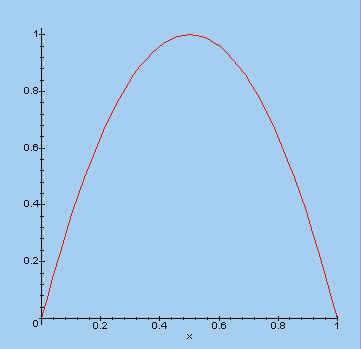
2. Iteraties
Vervolgens geven we een functie (procedure) f1 die een geordende verzameling punten (n, xn)
oplevert, waarbij xn de n-de iteratie is in:
xn+1 = l xn (1-xn)
De waarden van xn worden daarbij gegeven is 4 decimalen.
> fl := proc(labda, xstart, N) # xstart= startwaarde van x; N = aantal iteraties
> local A, k, x, S;
> A:=array[0..N];
> A[0]:=xstart;
> for k from 1 to N do
> x:=A[k-1];
> A[k]:=labda*x*(1-x);
> od;
> S:=seq([k,evalf(A[k],4)], k=0..N);
> RETURN(S);
> end:
Zodat
> s1 := fl(4, 0.2, 10);
s1 := [0, .2], [1, .64], [2,
.9216], [3, .2890], [4, .8219], [5, .5854], /
[6, .9708], [7, .1133], [8, .4020], [9, .9616], [10, .1478]
en bijvoorbeeld ook
> s2:=fl(4, 0.202, 10);
s2 := [0, .202], [1, .6448],
[2, .9162], [3, .3073], [4, .8514], [5, .5060], /
[6, .9999], [7, .0005741], [8, .002295], [9, .009159], [10, .03630]
Beide series, s1 en s2, kunnen, voor een beter overzicht, worden samengevoegd met
> s12:=seq( [s1[i][1], s1[i][2], s2[i][2]], i=1..11):
> for i to 11 do print( s12[i] ) od;
[0, .2, .202]
[1, .64, .6448]
[2, .9216, .9162]
[3, .2890, .3073]
[4, .8219, .8514]
[5, .5854, .5060]
[6, .9708, .9999]
[7, .1133, .0005741]
[8, .4020, .002295]
[9, .9616, .009159]
[10, .1478, .03630]
We maken nu een grafiek waarin we de series (s1 in blauw, s2 in rood) weergeven
> p_punten := plot( [s1], color=BLUE, style=POINT, symbol=BOX):
> p_lijnen := plot( [s1], color=BLUE ):
> w1 := display(p_punten, p_lijnen):
> p_punten := plot( [s2], color=RED, style=POINT, symbol=BOX):
> p_lijnen := plot( [s2], color=RED ):
> w2 := display(p_punten, p_lijnen):
> display(w1,w2);
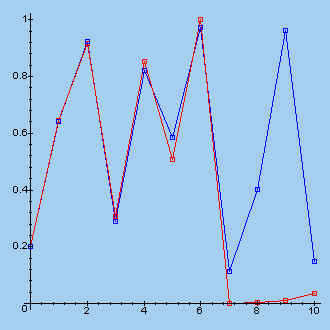
3. (On)regelmatig
verloop
De commando's uit pargraaf 2 kunnen we nu ook in een procedure plaatsen, waardoor we de
plot-commando's voor punten en lijnstukken bij verschillende startwaarden wat sneller en
overzichtelijker kunnen weergeven.
> makeplot := proc(name)
> local s1,s2;
> s1:=plot( name, style=point, symbol=box):
> s2:=plot( name ):
> RETURN(display(s1,s2));
> end:
Voor enkele waarden van l en x0 hebben we dan (bijvoorbeeld):
> s:=fl(0.9, 0.4, 30): makeplot([s]);
> s:=fl(2.9, 0.2, 30): makeplot([s]);
> s:=fl(3.03, 0.9, 30): makeplot([s]);
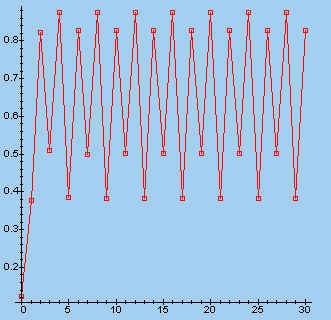
> s:=fl(3.5, 0.123, 30): makeplot([s]);
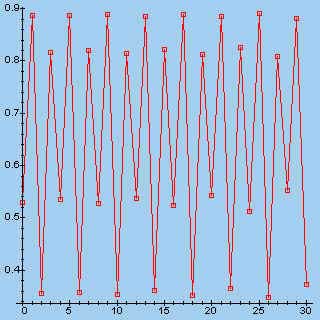
> s:=fl(3.564, 0.5301, 30): makeplot([s]);
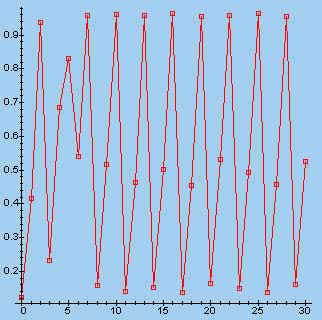
> s:=fl(3.853, 0.123, 30): makeplot([s]);
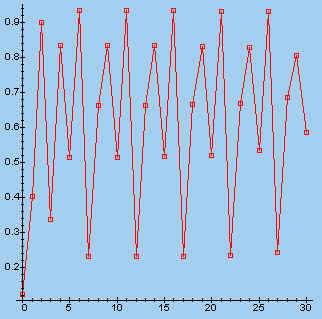
> s:=fl(3.7386, 0.123, 30): makeplot([s]);
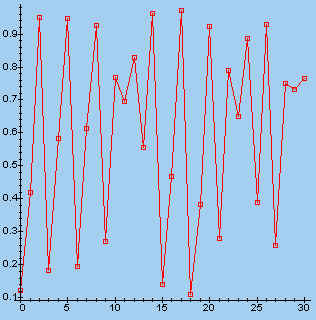
> s:=fl(3.9, 0.123, 30): makeplot([s]);
> s:=fl(3.99, 0.123, 30): makeplot([s]);
Let daarbij op het verloop van de puntenrij: convergentie, periodiciteit, maar ook volkomen onregelmatig.
| l = 0,9; x0 = 0,4 | l = 2,9; x0 = 0,2 | |
 |
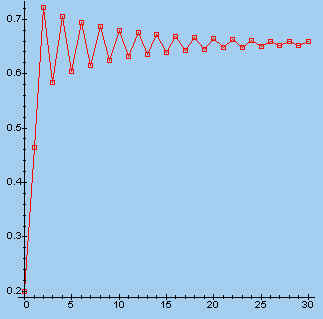 |
|
| l = 3,03; x0 = 0,9 | l = 3,5; x0 = 0,123 | |
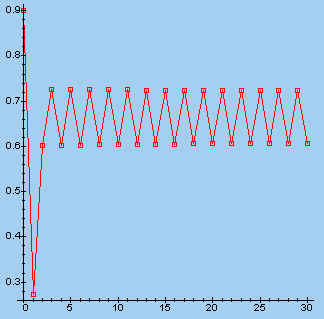 |
 |
|
| l = 3,564; x0 = 0,5301 | l = 3,853; x0 = 0,123 | |
 |
 |
|
| l = 3,7386; x0 = 0,123 | l = 3,9; x0 = 0,123 | |
 |
 |
|
| l = 3,99; x0 = 0,123 | ||
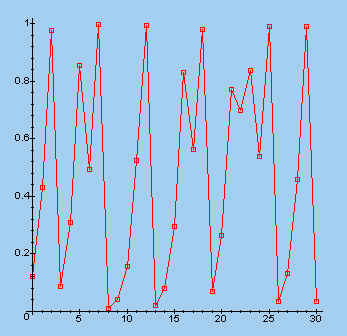 |
Zoals uit bovenstaande figuren blijkt, geven sommige waarden van lambda
een grillig verloop van de punten, terwijl andere aanleiding geven tot een regelmatig
patroon.
We laten hieronder nog enkele andere voorbeelden, alle met startwaarde x0 =0,1
volgen.
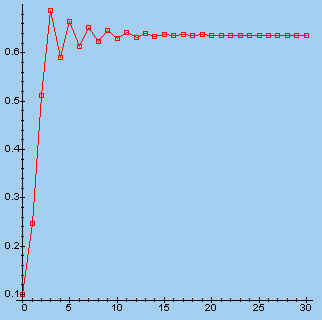
> s:=fl(2.75, 0.1, 30): makeplot([s]);
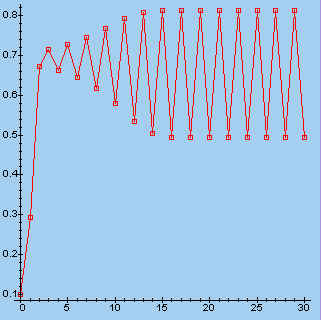
> s:=fl(3.25, 0.1, 30): makeplot([s]);
> s:=fl(3.5, 0.1, 30): makeplot([s]);
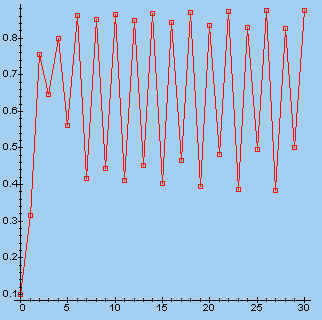
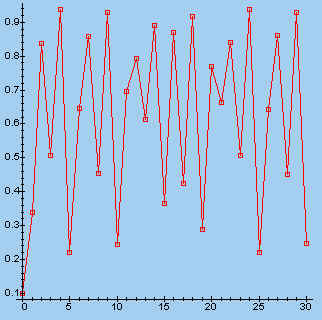
> s:=fl(3.75, 0.1, 30): makeplot([s]);
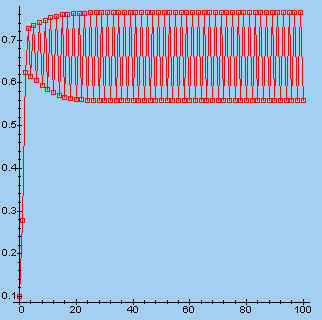
> s:=fl(3.1, 0.1, 100): makeplot([s]);
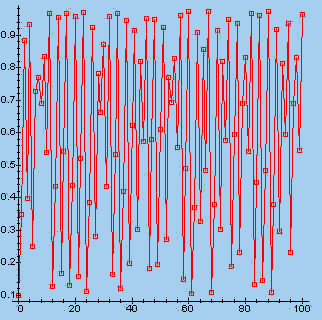
> s:=fl(3.888, 0.1, 100): makeplot([s]);
| l = 2,75 | l = 3,25 | |
 |
 |
|
| l = 3,5 | l = 3,75 | |
 |
 |
|
| l = 3,1 | l = 3,888 | |
 |
 |
[ De logistische functie (2) ] [ DK & Maple ]
[logistic1.htm] laatste wijziging op: 23-02-2001