Vraagstuk van Castillon

Overzicht  ][  Negatieve inversie | Inversie | Meetkunde

Overzicht terug

Probleemstelling en historie
Product van inversies cabrisignal
Een oplossing cabrisignal
Referenties

Download

Probleemstelling en historie terug

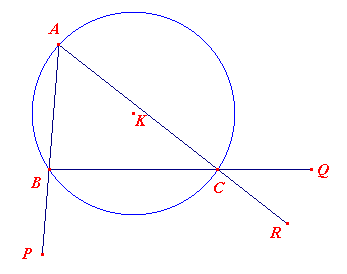
Gegeven zijn een cirkel K en drie vrijgelegen punten P, Q, R.
Construeer een in K ingeschreven driehoek ABC zo, dat AB door P, BC door Q en CA door R gaat.

cast1

De Zwitserse wiskundige Gabriel Cramer (1704-1752) legde het vraagstuk in 1742 voor aan de Italiaanse wiskundige Jean de Castillon (ook wel Johann Castillon), die het in 1776 oploste, althans publiceerde.
Castillon heette eigenlijk Giovanni Francesco Melchiore Salvemini (1709-1791), maar hij koos de naam Castillon naar zijn geboorteplaats Castiglione in Toscane.
Castillon gaf vanaf 1751 colleges (in wiskunde en astronomie) aan de Universiteit van Utrecht. In 1755 werd hij rector van die universiteit. In 1764 vertrok hij naar Berlijn om te gaan werken aan het Berliner Observatorium.
Ook van andere bekende wiskundigen, zoals Euler (1780), Lagrange (1776) en Poncelet (1844), is bekend dat zij oplossingen van het vraagstuk hebben gevonden. Pappos van Alexandrië (ca. 290-350) loste het probleem op in het geval dat de punten collineair zijn.

Product van inversies terug
Wanneer we twee of meer afbeeldingen na elkaar uitvoeren, spreken we van een product van afbeeldingen.
Het vraagstuk van Castillon kan om. met behulp van het product van drie inversies (zie de pagina "Inversie") waarbij de gegeven cirkel (niet-puntsgewijs) invariant is (zie pagina "Negatieve inversie"), worden opgelost.

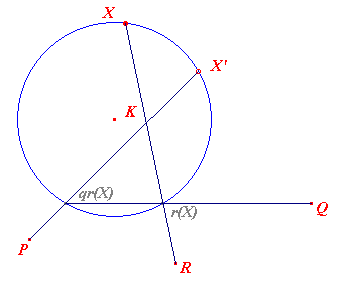
cast2a cast2b

In bovenstaande figuur, links, is het product van de inversies r, q, p (in deze volgorde: eerst r, dan q, en tenslotte p), resp. met centra R, Q, P toegepast op het punt X van de cirkel K:
X' = pqr(X)
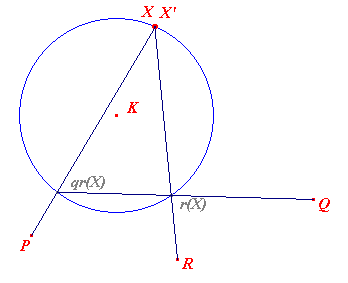
In bovenstaande figuur, rechts, valt het punt X' samen met punt X: X is een dubbelpunt van de afbeelding pqr.

Klik hier >Animatie< voor een illustratie van het bovenstaande met CabriJava .

Conclusie
We kunnen het vraagstuk van Castillon oplossen als we de dubbelpunten van de afbeelding pqr kunnen construeren.

Een oplossing terug

Definitie
Een afbeelding f (niet zijnde de identieke afbeelding) heet involutie, indien voor elk punt X geldt:
f(X) = X' en f(X') = X
Met andere woorden: f 2 (X) = X.
.
cast3 cast4

 

Volgens de genoemde definitie is de afbeelding pqr dan een involutie op de cirkel K
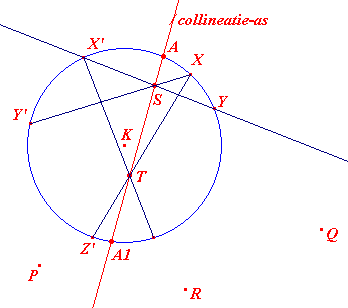
In bovenstaande figuur (links) zijn de puntenparen (X, X'), (Y, Y'), (Z, Z') origineel-beeldpunt van die involutie op K.
Uit de theorie der projectieve afbeeldingen is bekend, dat de snijpunten van elk tweetal lijnen XY' en X'Y op een (vaste) rechte lijn liggen, de collineatie-as.
Klik hier >Animatie< voor een CabriJavapplet waarin de collineatie wordt geïllustreerd.
Dus:
Indien S = XY' /\ XY en T = XZ' /\ X'Z, dan is ST de collineatie-as van de afbeelding pqr.
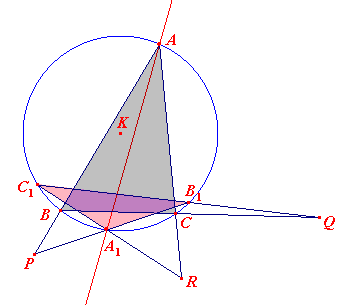
De constructie van ST is nu eenvoudig.
Construeer, uitgaande van drie punten X, Y, Z, de beeldpunten X', Y, Z' en bepaal de punten S en T.
De snijpunten A en A1 van ST met K zijn dan de dubbelpunten van de involutie pqr (zie bovenstaande figuur, rechts)
De punten B (cq. B1) en C (cq. C1) kunnen dan eenvoudig worden gevonden.¨

Opmerking
Er zijn dus maximaal twee oplossingen.

Maar, als de afbeelding pqr = I (waarbij I de identieke afbeelding is), dan zijn er oneindig veel oplossingen.
Dit laatste is zeker het geval, als de punten P, Q, R de hoekpunten zijn van een zogenoemde pooldriehoek van de cirkel K
Zie voor pooldriehoek de pagina "Pool en poollijn bij een cirkel".
Klik hier >Animatie< voor een CabriJavapplet waarin dit voor een pooldriehoek wordt geïllustreerd.
[einde Opmerking]

Referenties terug

[1]    M. BERGER: Geometry I, II. Berlijn: Springer Verlag (1996)
[2] O. BOTTEMA: Hoofdstukken uit de Elementaire Meetkunde. Utrecht: Epsilon Uitgaven (1997). pp. 70-71
[3] F. G.-M.: Excercises de Géométrie. Sceaux: Éditions Jaques Gabart (1991); herdruk uit 1920. pp. 20-22.
'F. G.-M.' staat voor 'Frère Gabriel-Marie', te weten Edmond Jéan-Antoine Brunhes, 1834-1916
[4] M. KINDT: Lessen in Projectieve Meetkunde. Utrecht: Epsilon Uitgaven (1996)
[5] J. PETERSEN: Methoden und Theorien zur Auflösung geometrischer Constructionsaufgaben. Kopenhagen: A.F. Høst & Sohn (1879); uit het Deens vertaald door R. von Fisher-Benzon. pp. 38-39.
[6] I.M. YAGLOM: Geometric Transformations I, III. New York: Random House, Inc. (1962); vertaling uit het Russisch.

Download terug
De figuren die gebruikt zijn bij de CabriJavapplets op deze pagina kunnen via deze website in één bestand worden gedownload.
Klik hier om het downloadproces te starten (ZIP-bestand, ca. 6 Kb)

begin pagina
[p: castillon.htm] laatste wijziging op: 24-07-2005