Algemene cisso´den
Overzicht ][ Cisso´de van Diokles | Meetkunde | Analyse
- Definitie en inleiding

- Eigenschappen
2.1. Twee cirkels / Limašon van Pascal (cardio´de)
2.2. Twee rechte lijnen
2.3. Rechte lijn en cirkel / Strofo´den / Trisectrix van Maclaurin / Concho´den
- Referenties
- Download
|
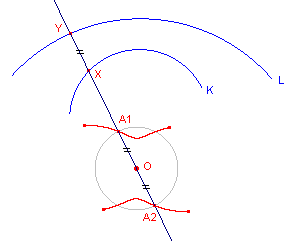
De cisso´de van twee cirkels bestaat in het algemeen uit ovalen van verschillende vorm, lemniscaten, en druppelvormige kromme lijnen. |
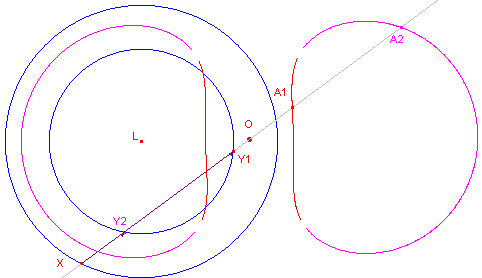 |
Hiernaast staat de cissoide van twee concentrische
cirkels met middelpunt L. Merk op, dat de delen niet-samenhangend zijn en dat de meetkundige plaats van A1 (schijnbaar?) overgaat in de meetkundige plaats van A2 en omgekeerd. De cisso´de van twee concentrische cirkels waarbij de pool samenvalt met het centrum, bestaat uit twee cirkels met de pool als middelpunt. |
Sommige algebra´sche krommen kunnen met een cisso´de-proces worden gegenereerd.
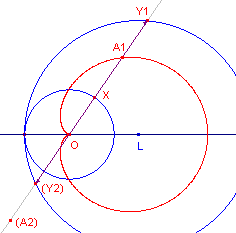 |
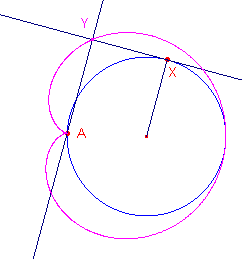
Limašon van
Pascal In de figuur hiernaast is een
cisso´de bepaald door twee inwendig rakende cirkels, waarbij de pool O samenvalt met het
middelpunt van de kleinste cirkel. |
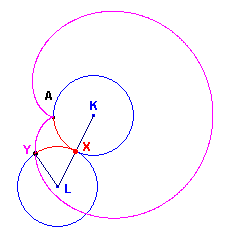 |
Opmerkingen [1] De limašon kan ook worden voortgebracht door een cirkel uitwendig rakend te laten rollen over een tweede even grote cirkel. Elk punt van de rollende cirkel beschrijft dan een limašon. De algemene naam voor een kromme die op deze manier wordt voortgebracht is epicyclo´de. Klik hier [2] De limašon (cardio´de) kan ook worden voortgebracht door een zogenoemd stangenmechanisme (Eng. linkage). Klik hier Voor andere stangenmechanismen zie verder Referenties. |
 |
[3] De hartlijn kan ook worden voortgebracht door uit te gaan van een vast punt A en een variabel punt X op de cirkel. De meetkundige plaats van het snijpunt Y van de raaklijn in X aan de cirkel en de loodlijn uit A op de raaklijn is dan de hartlijn. Opmerking |
|
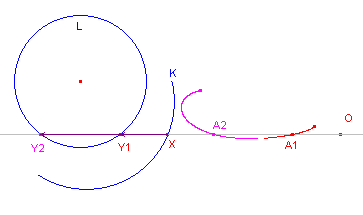
De cisso´de van twee snijdende rechte lijnen K en L is een hyperbool
(met de lijn L als Úen van de asymptoten). Ligt de pool op K, dan valt de cisso´de samen met K. |
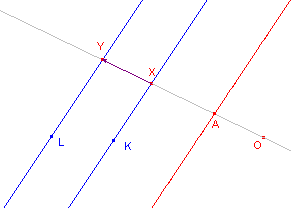 |
De cisso´de van twee evenwijdige lijnen K en L is een rechte lijn (evenwijdig met K en L). |
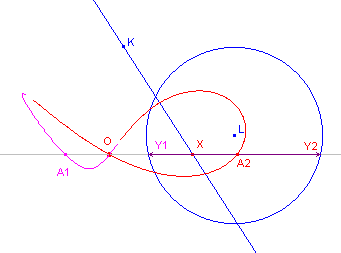 |
In het algemene geval wijkt de vorm van de cissoide bij een lijn K en een
cirkel L niet af van die voor twee cirkels (immers de lijn K is op te vatten als een
cirkel met "oneindig" grote straal). In de figuur hiernaast is K een rechte lijn en L een cirkel. |
 |
In de figuur hiernaast is K een cirkel en L een rechte lijn. |
Vanuit historisch oogpunt is de onderstaande ligging van pool en rechte lijn van belang.
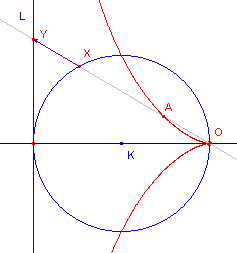 |
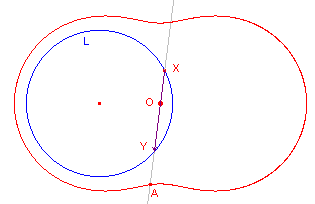
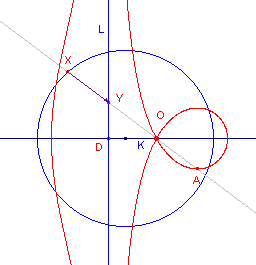
In de figuur hiernaast raakt de lijn L aan de cirkel K. Het punt O is het tegenpunt van het raakpunt aan de cirkel. De meetkundige
plaats heet cisso´de van Diokles. |
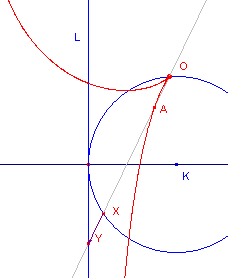 |
Ligt het punt O ergens anders op de cirkel dan is er sprake van een scheve cisso´de. |
 |
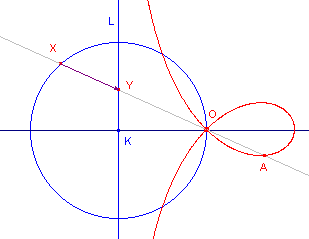 |
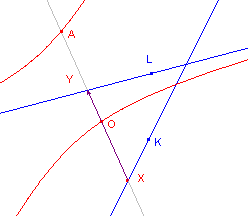
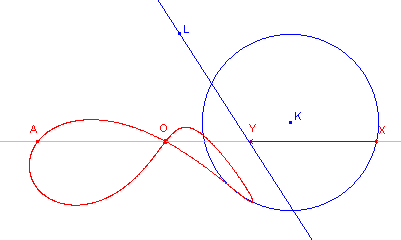
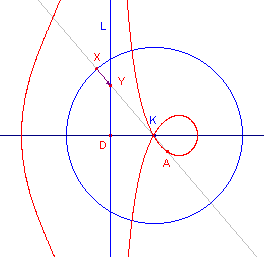
Strofo´den Als de lijn L de cirkel K snijdt en O op de cirkel ligt, worden de kromme lijnen strofo´de genoemd. De linker figuur heet scheve strofoţde; de rechter figuur heet strofo´de van Newton (rechte strofo´de). Bij de laatse gaat de lijn L door het middelpunt van K. |
| Klik hier |
||
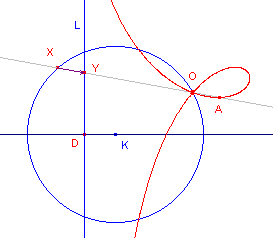
Een andere bijzondere strofo´de is de trisectrix van Maclaurin (Colin Maclaurin, 1698-1746, Schotland). ![]()
 |
L gaat hierbij door het midden van het lijnstuk KO. Kiezen we nu een punt P op de "lus" van de strofo´de, dan is PED = 3POD. Met deze strofo´de kan dus het probleem van de trisectie van een hoek worden opgelost (zie webpagina "Trisectie"). Nb. Het punt E ligt op 2/3 van OD. Het punt D is het beeld van C bij het cisso´de-proces. |
|
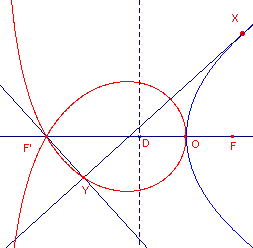
De trisectrix van Maclaurin kan ook ontstaan als zogenoemde voetpuntskromme. De kromme is namelijk ook de meetkundige plaats van de voetpunten van de loodlijnen uit het punt F ' op de raaklijnen in een willekeurig punt X van een parabool. Het punt F ' is dan het spiegelbeeld van het brandpunt F in de richtlijn (met voetpunt D) van de parabool. Opmerking Gemakkelijk is nu in te zien, dat DF ' = 2DO. [einde Opmerking] |
 |
 |
Concho´den Ligt het punt O op de loodlijn op de lijn L door het middelpunt van K (en niet op de cirkel), dan worden de kromme lijnen concho´de genoemd. Valt de pool samen met het middelpunt van K dan heet de kromme lijn concho´de
van Nicomedes |
| Klik hier |
||
Opmerkingen
[1]
De concho´de wordt vaker voortgebracht op de volgende manier.
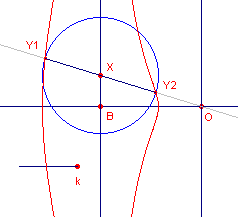 |
Een punt X wordt verplaatst over een rechte lijn loodrecht op de lijn OB. De punten Y1 en Y2 hebben een vaste afstand k tot X. De meetkundige plaats van de punten Y1 en Y2 is een concho´de. |
[2]
De concho´de van Nicomedes kan worden gebruikt bij het (niet-Euclidisch)
oplossen van het "Trisectie-probleem van een hoek".
Zie de pagina "Over de trisectie van een hoek" (met
CabriJavapplet).
[einde Opmerkingen]
3. Referenties
![]()
Voor referenties zie de webpagina "Cisso´de van Diokles".
Voor stangenmechanismen zie ook Peaucellier-cel en Rotator van Sylvester.
4.
Download ![]()
De meeste Cabri-figuren op deze pagina en de figuren die gebruikt zijn bij de CabriJavapplets,
kunnen in Úen bestand via deze website worden gedownload.
Klik hier om het downloaden te
starten (ZIP-bestand, ca. 18kB).