Cissoïde van Diokles

Overzicht ][ Algemene cissoïden | Geschiedenis | Meetkunde

0 .Overzicht terug

  1. Inleiding cabrisignal
  2. Gedurige evenredigheid
  3. Oplossing
  4. Een enkele eigenschap van de cissoïde cabrisignal
       4.1. De vergelijking van de cissoïde
       4.2. Een belangrijke eigenschap
       4.3. 2e Oplossing van het Delisch probleem
  5. Andere constructies van de cissoïde cabrisignal
       5.1. Voetpuntskromme van een parabool
       5.2. Constructie van Newton
       5.3. Beeld van een parabool bij inversie
       5.4. Spiegeling in een raaklijn
  6. Referenties
  7. Download

1. Inleiding terug
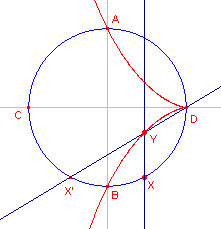
Diverse wiskundigen in de oudheid hebben het zogenoemde "Delisch probleem", de verdubbeling van de kubus, met andere dan Euclidische middelen (passer en liniaal) kunnen oplossen (zie ook de pagina "Trisectie").
Diokles (vermoedelijk eind 2e eeuw, begin 1e eeuw vChr.) heeft dit gedaan met behulp van een kromme lijn, de cissoïde.

figuur 1 cissoide1 Zijn AB en CD twee onderling loodrechte middellijnen van een cirkel.
X is een willekeurig punt van de cirkel.
X' is het spiegelbeeld van X in de lijn AB.
De loodlijn uit X op CD en de lijn DX' snijden elkaar in het punt Y.
Als X de cirkel doorloopt, dan doorloopt Y een kromme lijn.
Deze kromme lijn heet cissoïde van Diokles.

Opmerking
De naam "cissoïde" is afgeleid van het Griekse woord kissoeidhV (aangevuld met grammh), hetgeen betekent "lijn in de gedaante van een klimopblad" (kissoV = klimop).

Vermoedelijk is daarbij naar de vorm gekeken van het oppervlak ACBD begrensd door de cirkel en de kromme lijn, gelegen binnen de cirkel.
[einde Opmerking]

Klik hier cabrismall voor een CabriJavapplet bij het bovenstaande.

2. Gedurige evenredigheid terug
We bekijken de gedurige evenredigheid a : x = x : y = y : b.
x en y heten wel middelste evenredigen tussen a en b.
Dan volgt:
   x2 = ay
   y2 = bx
   xy = ab
Zodat x3 = axy = a2b.
Voor b = 2a hebben we dan: x3 = 2a3.
Als we dus in staat zijn (en dat zijn we, zie de paragraaf Oplossing) de lijnstukken x (en y) uit bovenstaande gedurige evenredigheid te construeren, dan is het lijnstuk x de ribbe van de kubus waarvan de inhoud twee keer zo groot is als de inhoud van de kubus met ribbe a.

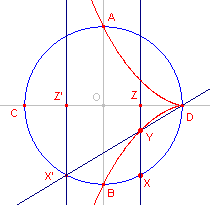
3. Oplossing terug
De cissoïde levert nu de constructie van de lijnstukken x en y uit de hierboven genoemde gedurige evenredigheid.

figuur 2 cissoide2 De lijnen XZ en X'Z' staan beide loodrecht op CD.
Dan is: XZ = X'Z' en DZ = CZ'.
Zodat
   DZ' : Z'X' = CZ : ZX ......(1)
Maar ook geldt:
   XZ2 = CZ . DZ (cirkeleigenschap)
of anders:
   CZ : ZX = ZX : DZ ......(2)
De driehoeken DZY en DZ'X' zijn gelijkvormig; daaruit volgt dan:
   DZ' : Z'X' = DZ : ZY ......(3)

Uit (1), (2) en (3) volgt dan
   CZ : ZX = ZX : DZ = DZ : ZY ......(4)

ZX en DZ zijn dus lijnstukken die middelste evenredigen zijn tussen CZ en ZY.

Constructie

figuur 3 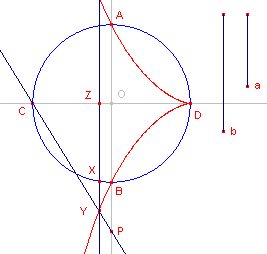cissoide3 We gaan ervan uit, dat de cissoïde als bovenstaand getekend is.
Construeer nu bij gegeven lijnstukken a en b op AB het punt P zodat
   CO : OP = a : b.
De lijn CP snijdt de cissoïde in Y (met YZ _|_ CD).
Uit de gelijkvormigheid van de driehoeken CZY en COP volgt dan:
   CZ : ZY = CO : OP = a : b
waaruit de noodzakelijke evenredigheid blijkt.
ZX en DZ zijn dus de gevonden lijnstukken.

Voor de rest van de constructie moeten nu de lijnstukken CZ, ZX, DZ en ZY naar evenredigheid worden vergroot.

Opmerking
Zie ook paragraaf 4.3, Oplossing van het Delisch probleem, voor een wat directere constructie.
[einde Opmerking]

4. Een enkele eigenschap van de cissoïde terug

4.1. De vergelijking van de cissoïde terug

figuur 4a 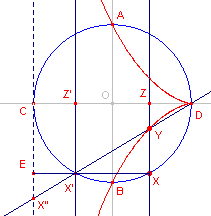cissoide4a Stellen we nu OZ = x, ZY = y en de straal van de cirkel gelijk aan R (Nb. x en y zijn andere waarden dan die hierboven zijn gebruikt).
We vinden uit de evenredigheid:
   CZ : ZX = DZ : ZY (zie paragraaf 3, uitdrukking 4)
dat
   CZ . ZY = ZX . DZ
of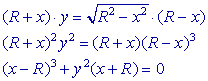
   cissoide_f1

De grafiek heeft een keerpunt bij x = R (in het punt D). De lijn x = -R (de loodlijn in C op CD) is verticale aymptoot van de grafiek.

4.2. Een belangrijke eigenschap terug
De lijn DX' snijdt de asymptoot van de kromme in het punt X".
Nu is:
   X'X" = DY
Bewijs:
Wegens de symmetrie in de lijn AB is CZ' = ZD. Dus X'E = DZ. Uit de congruentie van de driehoeken DZY en X'EX" volgt dan X'X = DY. ¨

Nb.
Deze eigenschap dient als "algemene definitie" voor een cissoïde.
Zie de pagina "Algemene cissoïden"

Gevolg
Uit deze eigenschap volgt een tweede manier om de cissoïde te construeren.

figuur 4b 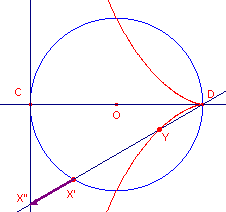cissoide4b X' is een willekeurig punt van de cirkel.
De lijn DX' snijdt de lijn in D loodrecht op de middellijn CD in het punt X'.
De meetkundige plaats van het beeld Y van het punt D bij de translatie over de (variabele) vector X'X" is nu de cissoïde van Diokles.

Klik hier Animatie voor een CabriJavapplet van deze constructie.

Deze constructie geeft een directe mogelijkheid een lijnstuk x te construeren waarvoor geldt, bij gegeven lijnstuk a, dat x3 = 2a3.
Zie hiervoor de paragraaf "2e Oplossing van het Delisch probleem".
  
figuur 4c 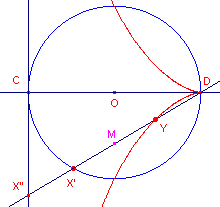cissoide4c Opmerking
De punten X' en Y liggen symmetrisch tov. het midden M van het lijnstuk DX".
Als we objecten in het punt M spiegelen, kunnen we andere eigenschappen van de constructie onderzoeken.
[einde Opmerking]

4.3. 2e Oplossing van het Delisch probleem terug
Let wel: de oplossing is niet mogelijk met passer en liniaal!

figuur 4d cissoide4d We gaan uit van een lijnstuk OA.
We construeren dan de "daarbij behorende" cissoïde (zie figuur 4d).
Het punt Oa is het spiegelbeeld van O in het punt A.
De lijn COa snijdt de cissoïde in het punt Y (niet construeerbaar met passer en liniaal).
De lijn DY snijdt de lijn OA in het punt M.
Nu geldt:
   OM3 = 2 OA3

5. Andere constructies van de cissoïde terug

5.1. Voetpuntskromme van een parabool terug
De cissoïde kan ook op een andere manier geconstrueerd worden.

figuur 5 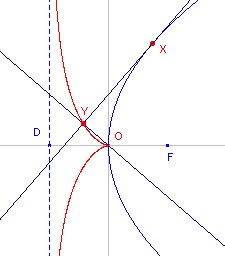cissoide5 We gaan daarbij uit van een parabool met brandpunt F en richtlijn door een punt D.
Het voetpunt van de loodlijn uit O op de raaklijn in punt X aan de parabool is het punt Y.
De meetkundige plaats van het punt Y is nu de cissoïde van Diokles.

Klik hier Animatie voor een CabriJavapplet voor deze constructie.

5.2. Constructie van Newton terug

figuur 6a 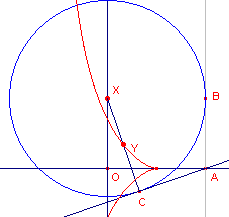cissoide_new1 We gaan uit van twee punten O en A.
Op de loodlijn in O op OA ligt een willkeurig punt X, dat middelpunt is van een cirkel met straal OA.
OB en OC zijn raaklijnen uit A aan de cirkel.
Het midden Y van OC beschrijft nu een cissoïde van Diokles.

Klik hier Animatie voor een CabriJavapplet voor deze constructie.

Gevolg

figuur 6b 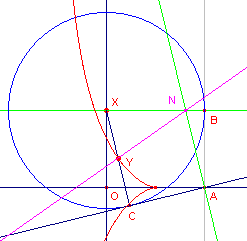cissoide_new2 Uit de constructie van Newton kunnen we de normaal van een punt van de cissoïde van Diokles eenvoudig vinden (zie ook bovenstaande CabriJavapplet).
De loodlijn in A op de raaklijn in C snijdt de loodlijn in B op de raaklijn in het punt N.
De lijn NY is nu normaal in Y aan de cissoïde.
figuur 6c cissoide_new3 Opmerking
De normalen van de cissoïde omhullen een parabool (zie figuur 6c).
Ook hieruit zien we dus dat de cissoïde de voetpuntskromme is van een parabool.
Nb. Het punt N in figuur 6b is niet het raakpunt van de normaal van de cissoïde aan de parabool!
Het punt A is niet het brandpunt van die parabool!
[einde Opmerking]

5.3. Beeld van een parabool bij inversie terug

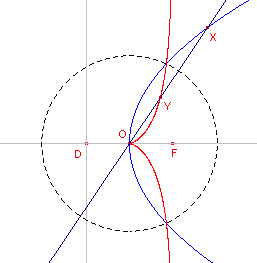figuur 7 cissoide6 Als centrum van inversie kiezen we de top van de parabool.
De inversiecirkel is willekeurig.

Klik hier Animatie voor een CabriJavapplet voor deze constructie.

5.4. Spiegeling in een raaklijn terug

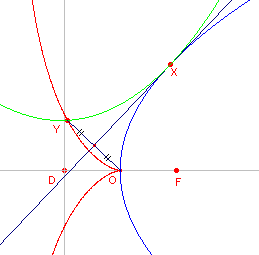figuur 8 cissoide7 De cissoïde kan ook ontstaan door spigeling van de top O in een raaklijn in het willekeurig punt X aan een parabool.
Of anders:
De meetkundige plaats van de top van een congruente parapool die uitwendig langs een parabool glijdt is een cissoïde ("roulette").

Klik hier Animatie voor een CabriJavapplet voor deze constructie.

6. Referenties terug

Webpagina "Over de trisectie van een hoek"
Webpagina "Algemene cissoïden"

[1] E.J. DIJKSTERHUIS: Vreemde woorden in de wiskunde, P. Noordhoff, Groningen (1948)
[2] TH. HEATH: A History of Greek Mathematics, volume I, Dover Publications, Inc. (reprint 1981)
[3] XAH LEE: A Visual Dictionary of Special plane curves (US)
[4] H. SCHUMANN, D. GREEN: Discovering Geometry with a Computer, Chartwell-Bratt, Bolton, GB (1994)
[5]    B.L. VAN DER WAERDEN: Ontwakende wetenschap, P. Noordhoff, Groningen (1950), pg.296-297

7. Download terug
De Cabri-figuren van deze pagina en de figuren gebruikt bij de applets kunnen in één bestand via deze website worden gedownload.
Klik hier om het downloaden te starten (ZIP-bestand, ca. 12Kb).

begin pagina

[cissoide.htm] laatste wijziging op: 02-08-01